18.5. Модель рынка с прогнозируемыми ценами.

В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Однако спрос и предложение в реальных ситуациях зависят еще и от тенденции ценообразования и темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функциями цены P(t).

Пример.

Пусть функции спроса d и предложения S имеют следующие зависимости от цены P и её производных:

1. Спрос d(t) “подогревается” темпом изменения цены если темп растет , то рынок увеличивает интерес к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с входит со знаком минус.

2. Предложение в еще большей мере усиливается темпом изменения цены, поэтому коэффициент при 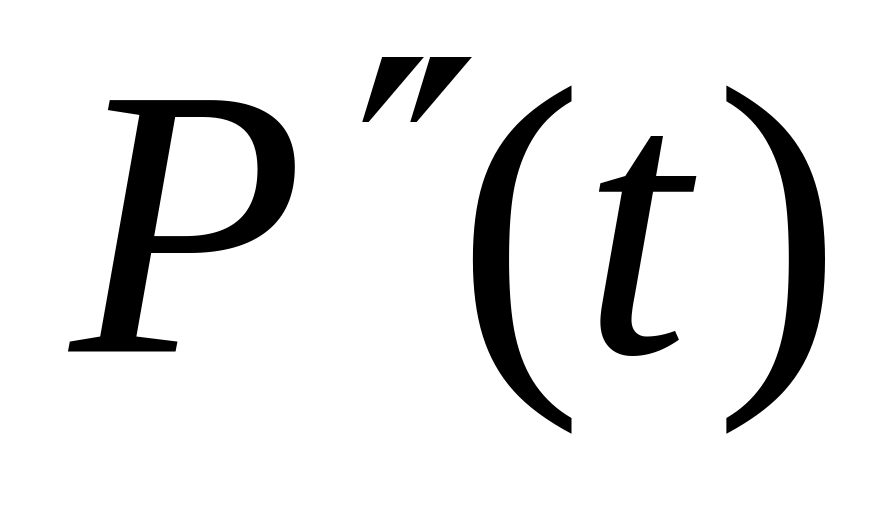в функции 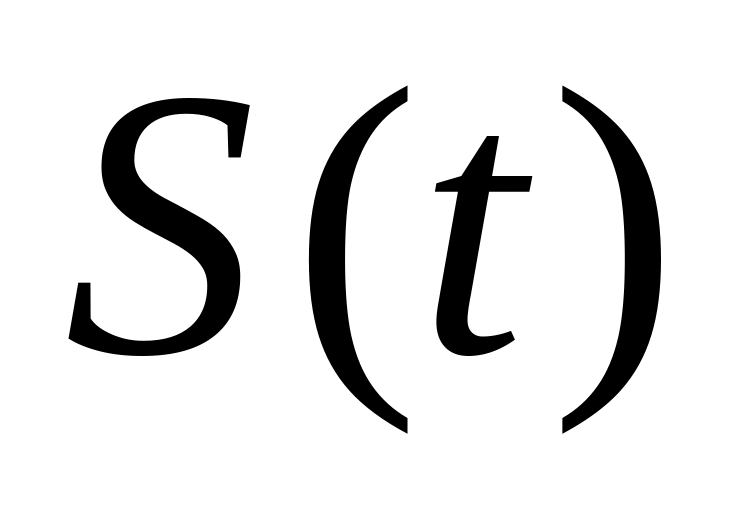больше, чем в . Рост цены также увеличивает предложение, поэтому слагаемое входит в со знаком плюс.

Требуется установить зависимость цены от времени. Поскольку равновесное состояние рынка характеризуется равенством , или (2).

Найдем общее решение однородного уравнения . Корни характеристического уравнения , , , и общее решение однородного уравнения , где и - произвольные постоянные. В качестве частного решения неоднородного уравнения возьмем , - постоянную величину как установившуюся цену. Подстановка в неоднородное уравнение дает .

Общее решение неоднородного уравнения (2) .

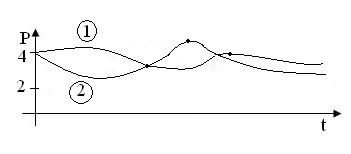
При , , т.е. все интегральные кривые имеют горизонтальную асимптоту P=3 и колеблются около неё. Это означает, что все цены стремятся к установившейся цене A=3 с колебаниями около неё, причем амплитуда этих колебаний затухает со временем.

Приведем частные решения задачи (2) в двух вариантах: задача Коши и смешанная задача.

1. Задача Коши с начальными условиями

, .

Решение задачи Коши имеет вид: .

2. Смешанная задача: в начальный момент времени известны цена и спрос: P(0)=4, d(0)=16. Из общего решения , используя условие P(0)=4 получим , откуда и . Теперь и . Отсюда и . Подставляя эти равенства во второе условие задачи d(0)=16 получим , откуда .

Решение задачи имеет вид: .

Изобразим интегральные кривые, соответствующие задачам 1 и 2 на рисунке.

Лекция 19. Производственные функции и их характеристики.

19.1.Производственные функции и их основные характеристики.

19.2.Оптимальное распределение ресурсов.

19.3.Максимизация прибыли производства продукции.

19.4.Модели поведения фирмы в условиях совершенной и несовершенной конкуренции.

19.1. Производственные функции и их основные характеристики.

Производственная функция (ПФ) – это функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных n равно числу ресурсов), а значения функции имеют смысл величин объемов выпуска , , n – факторная ПФ.

По экономическому смыслу , ,…, .

Для отдельного предприятия (фирмы), выпускающего однородный продукт, ПФ может связывать объем выпуска (в натуральном или стоимостном выражениях) с затратой рабочего времени по различным видам трудовой деятельности, различных видов сырья, комплектующих изделий, энергии, основного капитала. ПФ такого типа характеризуют действующую технологию предприятия (фирмы).

ПФ отражают зависимость результата производственной деятельности (выпуска продукции) от обусловивших его факторов производства (ресурсов). В рыночной экономике к ресурсам относятся также земля, капитал (основные фонды), труд и предпринимательская деятельность. Частными видами ПФ являются функции выпуска, которые отражают зависимость объема производства от наличия или потребления ресурсов, и функции издержек, отражающие зависимость издержек производства от объема продукции.

Ограничимся для простоты двумя ресурсами, то есть рассмотрим двухфакторную ПФ: .

Тип ПФ	ПФ	Параметры
Линейная		– предельный физический продукт, ,
Кобба – Дугласа		– фактор шкалы, , – эластичность выпуска продукции по отношению к затратам, ,
Затраты - выпуск		– количество затрат вида i, необходимое для производства одной единицы продукции.
С постоянной эластичностью замещения CES – функция		– коэффициент шкалы, , – коэффициент распределения, , , h – степень однородности, R>0, – коэффициент замещения,

Л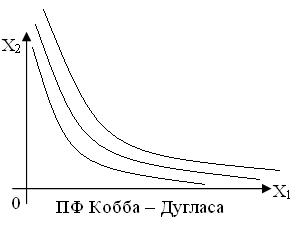 инии уровня ПФ называются изоквантами.

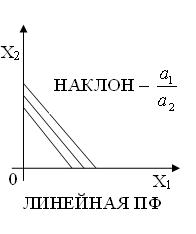
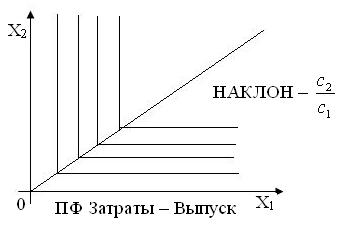
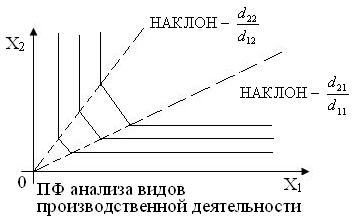
Основные характеристики ПФ:

1) , - средняя производительность i-го ресурса;

2) , - предельная производительность i-го ресурса;

3) , - эластичность выпуска по i-у ресурсу;

4) - эластичность производства;

5) - предельная норма замещения i-го ресурса j-ым, i,j =1,2.

Величина показывает, на сколько единиц увеличится объем выпуска продукции y, если объем затрат i-го ресурса вырастет на однy достаточно малую единицу при неизменных объемах другого затрачиваемого ресурса.

Величина показывает, на сколько процентов увеличится выпуск объема производства y, если затраты i-го ресурса увеличатся на 1% при неизменных объемах другого ресурса.

Для CES-функции эластичность производства E=h, , .