12.4. Геометрические приложения определенного интеграла.
1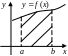
)
Вычисление площадей плоских фигур.
Если
.
Если
.
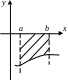
Е
сли
.
Если
.
Если фигура ограничена кривой, заданной параметрически, то есть
,
тогда
.
2) Вычисление длин друг кривых.
Пусть кривая L
задана явно, то есть
,
,
тогда длина
.
Если L
задана
параметрически
,
то
.
3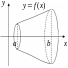
)
Вычисление объемов тел вращения.
Пусть , . Будем вращать кривую вокруг оси 0X, тогда объем тела, полученного при вращении кривой, вычисляют по формуле
.
Если же кривую
,
вращать вокруг оси
0Y, то
.
12.5. Несобственные интегралы.
Р
ассмотрим
.
Функция
определена на конечном промежутке
и ограничена на нем. Если нарушается
хотя бы одно из двух требований, то мы
имеем дело с несобственным интегралом.
1. Пусть нарушается требование конечности чисел a и (или) b. При этом возможны случаи:
1) пусть
определена на
и интегрируема на каждом конечном
промежутке
,
где
.
Несобственным
интегралом первого рода называется
и обозначается
,
то есть
(1).
Если предел в правой части равенства (1) существует и конечен, то несобственный интеграл называется сходящимся и его значение равно пределу правой части. В противном случае несобственный интеграл называется расходящимся.
2
)
пусть
определена на
и интегрируема на каждом конечном
промежутке
,
Несобственный
интеграл первого рода в этом случае
определяется по формуле
(2).
3) пусть
определена на
и интегрируема на каждом конечном
отрезке этого интервала, тогда
(3), причем несобственный интеграл в
левой части называется сходящимся, если
сходятся оба интеграла в правой части
равенства (3). Если хотя бы один из них
расходится, то расходится интеграл в
левой части.
Замечание.
Если
первообразная функции
на
,
тогда справедлива обобщенная формула
Ньютона-Лейбница
,
где
,
.
Пример.
2. Пусть нарушается требование ограниченности функции .
1) Пусть функция
непрерывна на
и
,
тогда
(4).
2) Если
непрерывна на
и
,
тогда
(5).
Интегралы в левой части равенств (4) и (5) называются сходящимися, если в правой части этих равенств предел существует и конечен и значение несобственного интеграла равно пределу правой части. Если в правой части равенств (4) и (5) пределы не существуют или бесконечны, то несобственные интегралы в левой части этих формул называются расходящимися.
3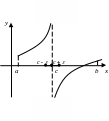
)
Если
непрерывна на
и
,
тогда
(6).
Интеграл в левой части равенства (6) называется сходящимся, если сходятся оба интеграла в правой части этой формулы; и расходящимся, если расходится хотя бы один из интегралов в правой части этой формулы.
Пример.
Установить сходимость интеграла
.
Так как
и
,
то есть
расходится, и потому данный интеграл
расходится.
Лекция 13. Дифференциальные уравнения первого порядка.
13.1. Определение дифференциального уравнения. Основные понятия.
13.2. Дифференциальные уравнения первого порядка. Основные понятия. Теорема существования и единственности решения.
13.3.Дифференциальные уравнения первого порядка с разделяющимися переменными.
13.4. Линейные дифференциальные уравнения первого порядка.
13.5. Однородные дифференциальные уравнения первого порядка.