7.4. Градиент функции.

Определение. Градиентом функции в точке называется вектор с координатами равными частным производным функции z в точке и обозначается .

Градиент функции указывает направление наискорейшего роста функции, а максимальная скорость роста функции равна модулю градиента.

Скалярное произведение равно производной функции по направлению в точке . Действительно Величина в правой части принимает наибольшее значение при , т.е. когда совпадает по направлению с . В свою очередь частные производные функции и является производными функции z в направлении координатных осей OX и OY.

;

.

7.5. Экстремумы функции двух переменных. Необходимое и достаточное условия существования экстремумов.

Пусть функция определена на множестве , точка является внутренней точкой множества D (принадлежит ему вместе с некоторой окрестностью)

Определение. Точка называется точкой локального максимума (минимума) функции , если существует окрестность точки , для всех точек которой при ( ).

Точки локального максимума и локального минимума называются точками экстремума функции.

Теорема (необходимое условие экстремумов).

Если функция в точке имеет экстремум и в точке

существуют частные производные функции z, то эти частные производные

равны нулю, то есть .

Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из

того, что ещё не следует, что - точка экстремума. Это точка лишь "подозрительная" на экстремум. Такие точки называют стационарными. Экстремумы функции могут находиться либо в стационарных точках, либо в точках, где частные производные не существуют.

Теорема. (достаточное условие существование экстремума)

Пусть функция имеет непрерывные производные второго порядка в некоторой окрестности стационарной точки , тогда, если , то - точка экстремума, причем при в точке локальный минимум, при -

локальный максимум; если , то - не является точкой экстремума.

Замечание. Если , то вопрос о существовании экстремума в точке остается открытым (используются другие методы исследования).

Пример. Найти экстремумы функции

, значит в точке А экстремума нет; и , значит в точке В локальный минимум

Лекция 8. Метод наименьших квадратов.

8.1. Метод наименьших квадратов

8.2.Применение метода наименьших квадратов (случай линейной зависимости).

8.3. Использование метода наименьших квадратов на фондовой бирже.

8.1. Метод наименьших квадратов.

Рассмотрим систему линейных уравнений (1) 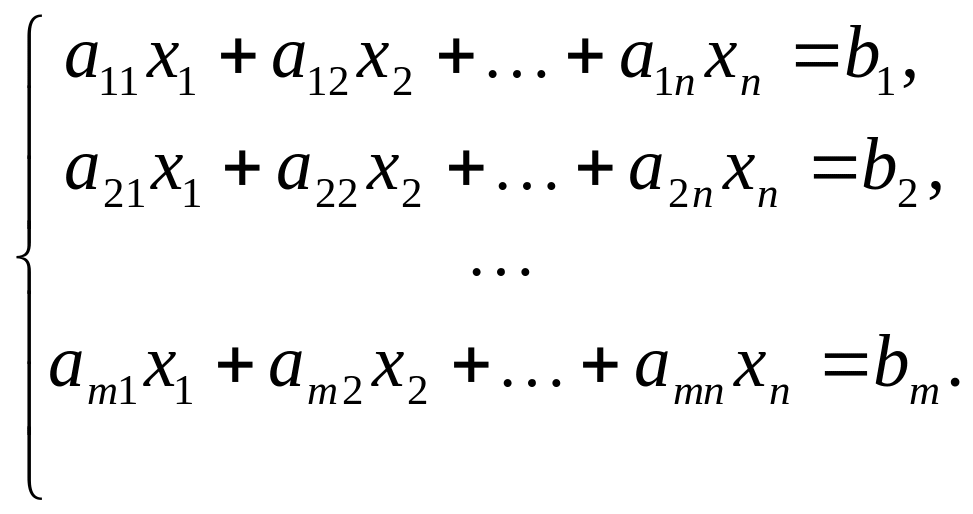Предположим, что система (1) является результатом исследования, а вектор 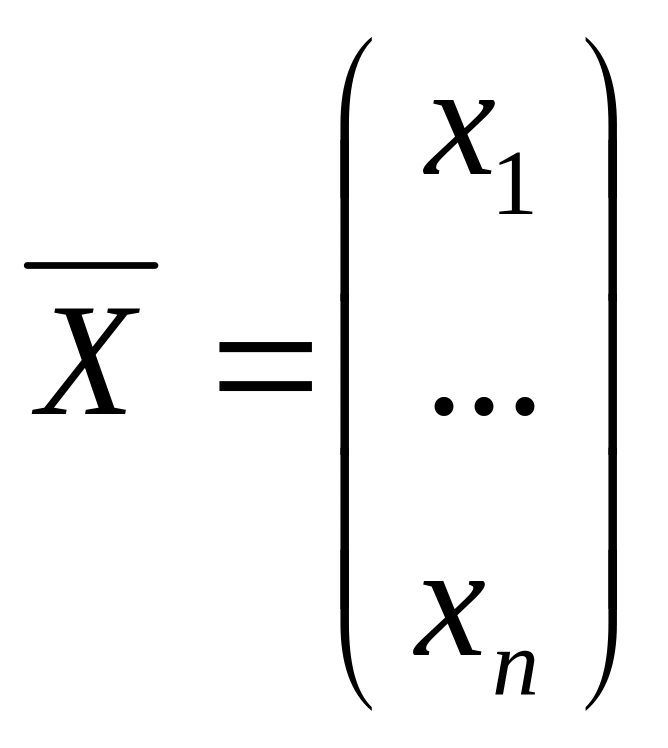– результатом практических наблюдений. В каком случае можно утверждать, что фактические данные подтверждают теорию?

Случаи, когда удовлетворяет системе (1), то есть подтверждает теорию, встречаются редко. Будем считать, что не опровергает теорию, если является хотя бы примерным решением системы (1). В таком случае разность – является ошибкой системы. Ошибку S(x) всей системы (1) можно определить по крайней мере одним из трех способов:

1.

2.

3. .

Алгоритм поиска наименьшего значения функции , то есть наименьшей ошибки, является наиболее простым в первом случае, что объясняет популярность метода наименьших квадратов. Метод наименьших квадратов широко используется при анализе статических данных для выявления функциональной зависимости между наблюдаемыми величинами, причем количество наблюдаемых величин не имеет принципиального значения.