19.2. Оптимальное распределение ресурсов.

Линии уровня ПФ - изокванты позволяют геометрически иллюстрировать решение задачи об оптимальном распределении ресурсов.

На рисунке линии уровня изображены сплошными линиями, а штриховкой выделена так называемая экономическая область, которая характеризуется тем, что высекаемые ею части изоквант представляют собой графики убывающих функций, т.е. увеличение количества одного фактора позволяет уменьшить количество другого, не меняя размера выпуска. Иными

словами, экономическая область – это множество значений факторов,

допускающих замещение одного из них другим.

П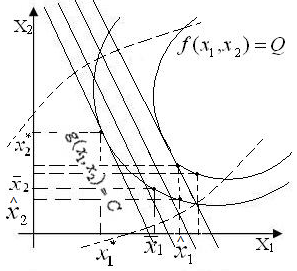 усть - функция издержек, характеризующая затраты, необходимые для обеспечения значений ресурсов x₁ и x₂, будем считать, что функция издержек линейная:

, где p₁ и p₂ – “цены” факторов x₁ и x₂. Комбинации линий уровня функций и позволяют делать выводы о предпочтительности того или иного значения факторов . Например, пара значений более предпочтительна, чем пара , так как обеспечивает тот же выпуск, но с меньшими затратами. Оптимальными значениями факторов будут значения - координаты точки касания линии уровня функции выпуска и функции издержек.

19.3. Максимизация прибыли производства продукции.

Пусть - количества производимых m разновидностей товара , а их цены – соответственно (все - постоянные величины). Пусть затраты на производство этих товаров задаются функцией издержек . Тогда функция прибыли имеет вид:

Максимум прибыли естественно искать как условие локального экстремума функции многих переменных при : , .

Это условие приводит к системе алгебраических уравнений относительно переменных : , (1).

Система уравнений (1) реализует известное правило экономики: предельная

стоимость (цена) товара равна предельным издержкам на производство этого товара. Сам процесс нахождения решения системы уравнений (1) зависит от вида функции издержек и может быть достаточно сложным.

Пример. Пусть производятся два вида товаров, их количества x₁ и x₂. Пусть P₁=8, P₂=10 – цены на эти товары соответственно, а - функция затрат. Тогда прибыль является функцией двух переменных .

Необходимые условия локального экстремума приводит к системе уравнений , решением которой является точка (2,4). Так как , то найденная точка (2,4) определяет локальный максимум функции прибыли .

Функция прибыли обычно вычисляется по формуле , (2) где F(K,L) – производственная функция, P – цена продукции, W и R – соответственно факторные цены на труд и капитальные затраты, L – затраты трудовых ресурсов, K – затраты капитала. Рассмотрим две задачи связанные с определением максимума прибыли.

1. Точка (K₀,L₀)называется оптимальным планом, если в ней функция прибыли (2) принимает максимальное значение. Найти предельную норму замещения производственной функции F при оптимальном плане. В точке локального экстремума . Предельная норма замещения вычисляется по формуле , откуда при оптимальном плане получим .

2. Максимизация функции прибыли. Найти оптимальный план и максимум функции прибыли (2), если производственная функция .

В данном случае функция прибыли имеет вид .

Необходимые условия локального экстремума и приводят к системе линейных алгебраических уравнений относительно координат K₀ и L₀ оптимального плана 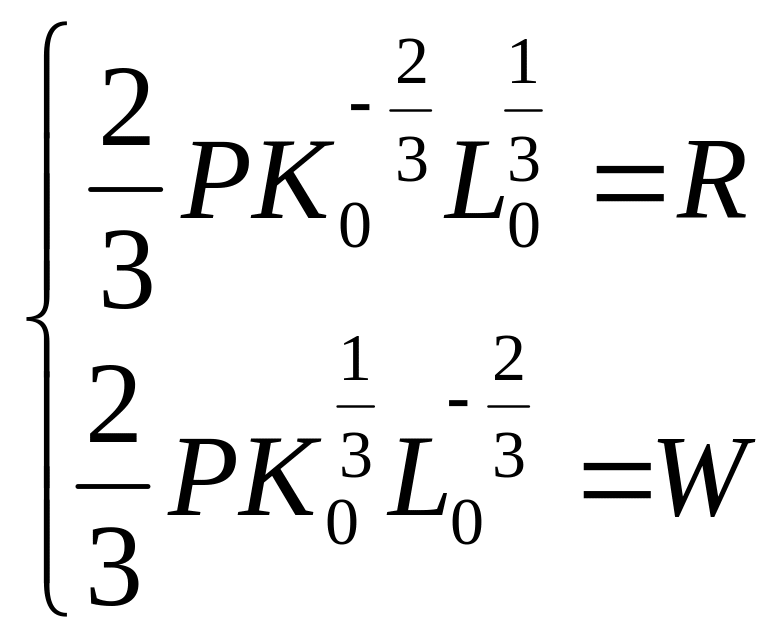, при этом , откуда получим координаты оптимального плана , .

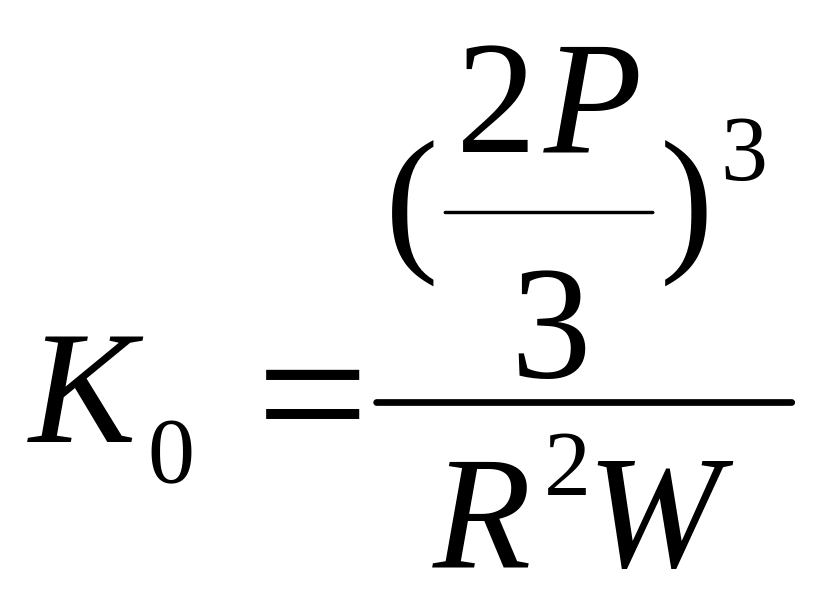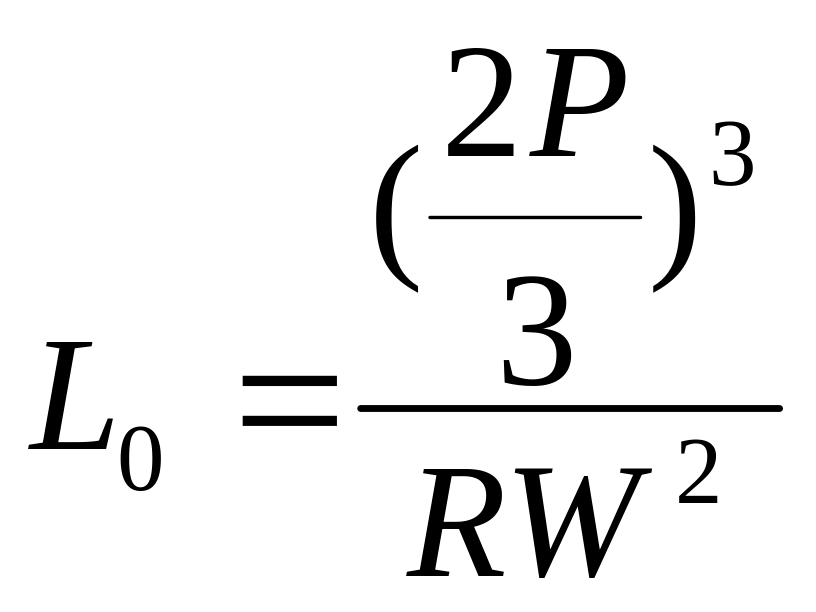Подстановка этих величин в функцию прибыли дает её максимум .