2.1.Свойства связей

В

Рис. 2.1. Схема кинематической пары шар-плоскость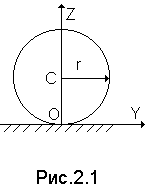

классической механике связями называют ограничения, налагаемые на положения и скорости точек механической системы, которые должны выполняться при любых действующих на систему силах. Они могут быть записаны в виде уравнений или неравенств. Уравнения, которым в силу наложенных связей должны удовлетворять координаты точек механической системы и их скорости (первые производные от координат по времени), называются уравнениями связей. Самыми распространенными в механизмах являются геометрические связи, которые ограничивают относительные перемещения звеньев и уравнения которых содержат только координаты точек (и, может быть, время). Такие связи имеют все кинематические пары и кинематические соединения с твердыми промежуточными элементами. Например, кинематическая пара типа шар-плоскость (рис.2.1) накладывает на относительное движение звеньев одну геометрическую связь, уравнение которой Z_с – r = 0. Из уравнения связи следует, что ликвидировано относительное перемещение звеньев вдоль оси Z. Так как число связей S=1, то подвижность пары H = 6 – S = 5. Число обобщенных координат, однозначно определяющих положение шара на плоскости, также равно пяти.

Кроме геометрических связей, в механизмах могут быть дифференциальные (кинематические) связи, уравнения которых содержат координаты точек и производные от этих координат по времени (и, может быть, время). Если эти уравнения интегрируются, то дифференциальная связь приводится к геометрической. Дифференциальные интегрируемые и геометрические связи называются голономными связями. Дифференциальные связи, уравнения которых не могут быть проинтегрированы, являются неголономными связями. Неголономные связи появляются в кинематических парах при учете трения.

О

Рис. 2.2. Схема фрикционного механизма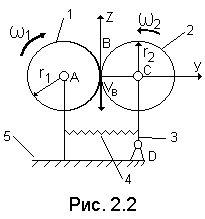

собое место занимает фрикционная пара. Рассмотрим фрикционную передачу (рис.2.2), состоящую из цилиндрических катков 1 и 2, стержня 3, стойки 5 и пружины 4, которая не входит в число звеньев и предназначена для обеспечения необходимого прижатия катков. Выясним, какие связи накладывает высшая кинематическая пара В, которая образуется в месте соприкосновения катков. Цилиндрические колеса соприкасаются по общей образующей, совпадающей с осью Х, проходящей перпендикулярно плоскости чертежа. Кинематическая пара ликвидирует перемещение вдоль оси У и вращение вокруг оси Z, накладывая две геометрические связи. Если трение между катками настолько велико, что нет проскальзывания, то наложена еще одна (дифференциальная) связь. Уравнение этой связи следует из кинематического условия Vв = ω₁r₁ = ω₂r₂.

Интегрируя и принимая, что в начале φ₁ = 0 и φ₂ = 0, получаем

φ₂ = φ₁r₁/r₂. Полученное уравнение связи выражает зависимость между угловыми перемещениями колес и имеет вид геометрической связи. Известно, что передача движения во фрикционной передаче обусловлена упругим скольжением деформированных участков катков, поэтому приведенное уравнение связи можно рассматривать только как первое приближение к действительному. С учетом упругого скольжения φ₂ = φ₁r₁ (1-£)/r₂, где £ – коэффициент скольжения, зависящий от силы прижатия катков, материала катков и вида смазочного материала. Во втором приближении коэффициент скольжения £ считается постоянным (определяется опытным путем). Второе приближение оказывается достаточно точным в инженерных расчетах при оценке сил и прочности в передаче ('' Детали машин ''). Ввиду малости коэффициента £ (0,03…0,001) для кинематического анализа обычно достаточно и первого приближения. Связь, обусловленную трением между катками во фрикционной передаче, называют псевдокинематической 5.

Кроме голономной или неголономной связь может быть удерживающей или неудерживающей, стационарной или нестационарной. Связи, в уравнения которых время явно не входит, называют стационарными. В уравнение нестационарной связи время входит в явной форме. Удерживающими называют связи, при наличии которых для любого возможного перемещения точки механической системы противоположное ему перемещение также является возможным. Удерживающие связи описываются равенствами, а неудерживающие - неравенствами. Неудерживающие связи характерны для гибких звеньев, например, гибкие связи между звеньями 1 и 3 (рис.1.9, г) не препятствуют сближению звеньев, но делают невозможным противоположное относительное перемещение.

В курсе «Теория механизмов» рассматриваются механизмы с голономными, стационарными и удерживающими связями. В механизмах связи обычно действуют постоянно. Однако существуют механизмы переменной структуры, в которых связи, оставаясь стационарными, изменяются в какой-то момент времени. Например, в планетарной коробке скоростей из одного зубчатого механизма с несколькими степенями свободы путем включения элементов управления (муфт и тормозов) получают несколько различных по строению механизмов с одной степенью свободы. Другим примером механизма переменной структуры может служить рассмотренный ранее (рис.2.2) фрикционный механизм, в котором при недостаточной силе прижатия катков начинается буксование: входное звено вращается, а выходное - неподвижно.