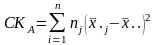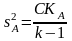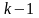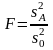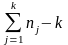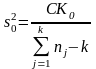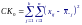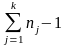22. Дисперсионный анализ. Цель и задачи дисперсионного анализа.

Наиболее часто приходится решать задачи, связанные со сравнением более двух средних. В их основе лежит дисперсионный анализ, разработанный Фишером.

Общая задача дисперсионного анализа включает несколько факторов, каждый из которых имеет не менее двух уровней.

В основе каждой задачи лежит план эксперимента, т. е. правило соотнесения каждого наблюдения исследуемой величины с определенной комбинацией рассматриваемых факторов, и модель дисперсионного анализа, т. е. математическое соотношение, представляющее наблюдение в виде суммы математического ожидания и ошибки: наблюдаемое значение = Sпараметры, описывающие определяемые эффекты +

Sслучайные величины, описывающие неопределенные эффекты.

Дисперсионный анализ основан на следующих допущениях относительно случайных величин, описывающих неопределенные (остаточные) эффекты:

• Математическое ожидание каждой остаточной случайной величины равно нулю

• Остаточные случайные величины независимы

• Все остаточные случайные величины имеют одинаковую дисперсию

• Каждая остаточная случайная величина распределена по нормальному закону

23. Однофакторный дисперсионный анализ

Рассмотрим простейший случай дисперсионного анализа, когда изучается влияние на исследуемую величину какого-либо одного фактора A. Будем считать, что фактор A изучается на k уровнях A₁, A₂, ..., A_k. Пусть для простоты рассмотрения на каждом уровне производится одинаковое число n наблюдений исследуемой величины.

Результаты наблюденных значений можно представить в виде таблицы:

Задачей дисперсионного анализа является выяснение вопроса о существенности влияния фактора A на величину X, т. е. вопроса о том, значимо ли отличаются между собой выборочные средние для каждой группы данных.

Для этого необходимо проверить нулевую гипотезу H₀: μ₁ = μ₂ = ... = μ_k против альтернативной гипотезы

H₁ : не все μ_j равны.

Чем больше разброс средних и чем меньше разброс значений внутри групп, тем меньше вероятность

того, что наши группы ─ это случайные выборки из одной совокупности.

Сформулируем это суждение количественно.

Совокупность данных по столбцам таблицы (уровням фактора или группам) при справедливости нулевой гипотезы можно рассматривать как одну выборку объема n х k из генеральной совокупности с математическим ожиданием μ и дисперсией σ²

Оценка генерального среднего:

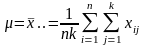
Н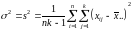 есмещенная оценка дисперсии генеральной совокупности:

Кроме того, дисперсию совокупности можно оценить во-первых на основании групповых дисперсий. Такая оценка не будет зависеть от различий групповых средних. Во-вторых, разброс выборочных средних тоже позволяет оценить дисперсию совокупности. Понятно, что такая оценка дисперсии зависит от различий выборочных средних.

При справедливости нулевой гипотезы любая из выборочных дисперсий дает одинаково хорошую оценку. Поэтому в качестве оценки дисперсии генеральной совокупности возьмем среднее выборочных дисперсий. Эта оценка называется внутри групповой дисперсией:

О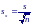 ценим теперь дисперсию совокупности по выборочным средним. Поскольку мы предположили, что все выборки извлечены из одной совокупности, то стандартное отклонение выборочных средних будет служить оценкой ошибки среднего:

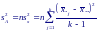
Отсюда находим межгрупповую оценку дисперсии:

При справедливости нулевой гипотезы оценки s², s_A² , s₀² являются несмещенными оценками генеральной дисперсии σ². Посмотрим, как ведут себя оценки s², s_A², s₀² при нарушении нулевой гипотезы. Найдем математические ожидания каждой дисперсии для такого случая.

О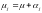 тклонение от нулевой гипотезы означает, что математическое ожидание в j-й группе может быть представлено в виде:

μ – генеральное среднее (математическое ожидание); α_j – дифференциальный эффект для уровня j

Тогда модель дисперсионного анализа будет иметь вид:

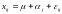
О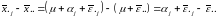 тсюда следует, что:

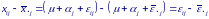
П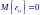 ри справедливости допущений:

1. для всех i и j

2. с 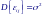лучайные величины ε_ij взаимно независимы

3. для всех i и j

М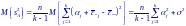 атематическое ожидание межгрупповой дисперсии s_A:

а математическое ожидание внутригрупповой дисперсии s₀:

Таким образом, при несправедливости нулевой гипотезы оценка s_A² является смещенной, при этом смещение определяется суммой квадратов дифференциальных эффектов групп (уровней фактора). Это означает, что при нарушении нулевой гипотезы оценка s_A² будет иметь тенденцию к возрастанию и тем большую, чем больше отклонение от этой гипотезы.

В результате задача проверки гипотезы H₀ сводится к проверке гипотезы о равенстве дисперсий s_A² и s₀². При справедливости допущения о нормальном распределении случайных величин ε_ij отношение:

в случае справедливости нулевой гипотезы подчиняется F-распределению с l₁ = k-1 и l₂ = k(n-1) числом степеней свободы.

Влияние фактора A на исследуемый признак считается значимым с уровнем значимости α, если

т. е. когда расчетное значение статистики F превышает значение α-процентной точки распределения Фишера.

Если это условие не выполняется, то влияние фактора A на исследуемую величину считается незначимым, т.е. математические ожидания μ₁, ...,μ_k имеют общее генеральное среднее (математическое ожидание) μ,. С другой стороны, если гипотеза H₀ отвергается, то делается вывод о том, что некоторые или все μ_j не совпадают.

Обобщим дисперсионный анализ на случай неравной численности групп.

Полная сумма квадратов отклонений значений x_ij от оценки генерального среднего будет определяться выражением:

П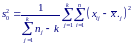 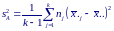оскольку сумма квадратов между группами СК_A имеет k − 1 степеней свободы, а сумма квадратов внутри групп СК₀ имеет ∑n_j − k степеней свободы, то оценки межгрупповой (факториальной) и внутригрупповой (остаточной) дисперсий имеют соответственно вид:

Результаты дисперсионного анализа в общем случае обычно представляют в виде следующей таблицы