16. Проверка гипотезы о равенстве двух средних зависимых нормальных выборок

Необходимо при уровне значимости α проверить гипотезу H₀: m_x1 = m_x2, т. е. гипотезу о равенстве математических ожиданий совокупностей, при альтернативной гипотезе H₁: m_x1 ≠ m_x2

В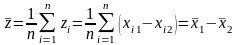 ведем в рассмотрение случайную величину Z, которая принимает значения z_i = x_i1 − x_i2. Выборочное среднее случайной величины Z:

Случайная величина z как разность двух нормально распределенных случайных величин тоже распределена по нормальному закону с нулевым математическим ожиданием при справедливости нулевой гипотезы. Статистикой критерия проверки нулевой гипотезы служит величина:

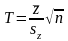
Статистика T распределена по закону Стьюдента с числом степеней свободы n−1.

Гипотеза H₀ не отвергается, если значение статистики:

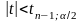
17. Ранги и ранжирование

Рангом наблюдения называют тот номер, который получит это наблюдение в упорядоченной совокупности всех данных после их упорядочения по определенному правилу, например от меньших значений к большим или наоборот.

Например пусть выборка состоит из чисел: 6; 17; 14; 5; 12. После упорядочивания данных имеем: 5; 6; 12; 14; 17. Тогда ранг числа 5 равен 1, числа 6 – 2, числа 12 – 3 и т. д.

Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием.

Статистические критерии, в которых делаются выводы на основании рангов данных, называются ранговыми критериями.

Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. В этом случае обычно используют средние ранги.

Средние ранги вводятся следующим образом:

• Предположим, что наблюдение x_i имеет ту же величину, что и некоторые другие из общего числа n наблюдений.

• Эту совокупность одинаковых наблюдений в выборке называют связкой. Количество таких одинаковых наблюдений в связке называют ее размером.

• Средний ранг наблюдения x_i в ранжированной выборке – это среднее арифметическое тех рангов, которые были бы назначены x_i и всем остальным элементам связки, если бы одинаковые наблюдения оказались различными.

Например пусть выборка состоит из чисел: 6; 17; 12; 6; 12. После упорядочивания данных имеем: 6; 6; 12; 12; 17. Тогда рангами первых двух чисел будут 1 и 2, вторых 3 и 4, последнего – 5. Следовательно, средние ранги для значений 6 и 12 равны соответственно:

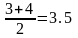
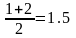
В результате ранжирования данные имеют вид: 1.5; 5; 3.5; 1.5; 3.5.

18. Непараметрический критерий Вилкоксона для проверки однородности двух независимых выборок.

Критерий Вилкоксона предназначен для проверки гипотезы об однородности двух независимых выборок.

Предположим, что имеются две независимые выборки x₁, x₂,…, x_m и y₁, y₂,…, y_n. Нулевая гипотеза заключается в предположении, что обе выборки извлечены из одной и той же генеральной совокупности и, значит, функции распределения случайных величин X и Y одинаковы. Эту гипотезу можно записать следующим образом:

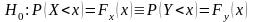
Не ограничивая общности рассмотрения, предположим, что n ≤ m, в противном случае X и Y следует поменять местами

Рассмотрим ранги элементов объединенной выборки. Для их получения совокупность всех наблюдений следует упорядочить в порядке возрастания. Будем считать, что в совокупности случайных величин X и Y нет совпадающих значений и, следовательно, результат упорядочения однозначен.

Последовательность рангов совокупности объема m + n является перестановкой чисел 1, 2,…,m + n. Поэтому возможное число ранговых последовательностей – это совокупность перестановок чисел 1, 2,…,m + n.

Их общее число равно (m + n)!

Если исходные данные однородны, т. е. наблюдения в выборке независимы и одинаково распределены, то в качестве последовательности рангов с равными шансами может появиться любая перестановка чисел от 1 до m + n. Поскольку таких перестановок (m + n)!, то вероятность каждой перестановки равна 1/(m + n)!. Этот результат не зависит от закона распределения самих наблюдений.

Рассмотрим, как будет изменяться распределение вероятностей среди ранговых последовательностей, т. е. среди перестановок, при отступлении от однородности выборок. В качестве нарушения однородности будем рассматривать следующие альтернативные гипотезы:

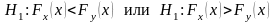
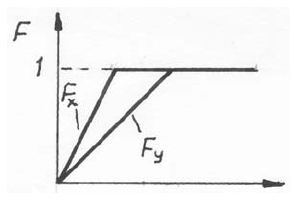
В этом случае F_x(x) > F_y(x) т. е. P(X < x) > P(Y < x), а значит, наблюдения из второй выборки имеют тенденцию превосходить наблюдения из первой. Поэтому ранг наблюдений из второй выборки будет чаще принимать значения из правой части ряда чисел

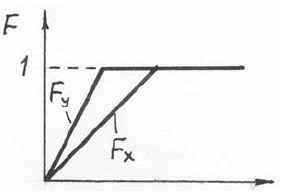
В этом случае F_x(x) < F_y(x), следовательно ранги наблюдений из второй выборки будут чаще принимать значения из левой части ряда чисел 1, 2,…,m + n.

Следовательно, ранги в какой-то мере могут характеризовать, например, положение одной выборки по отношению к другой, и в то же время они не зависят от неизвестных распределений выборок. Это обстоятельство и положено в основу ранговых методов.

В критерии Вилкоксона в качестве в качестве статистики используется случайная величина:

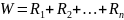
Здесь R_j – ранги наблюдений второй выборки в общей объединенной выборке.

П ри нулевой гипотезе H₀ вероятность каждого упорядоченного набора рангов наблюдений второй выборки R₁, R₂,…,R_n одна и та же и равна:

Отсюда для каждой пары значений m и n можно рассчитать распределения статистики W.

Д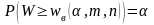 ля проверки с уровнем значимости α гипотезы H₀ об однородности выборок при альтернативной гипотезе H₁: F_x(x) > F_y(y) по имеющимся таблицам находят верхнее критическое значение w_в(α, m, n) статистики W, т. е. такое значение, для которого:

Гипотезу об однородности выборок следует отвергнуть с уровнем значимости α, если рассчитанное значение статистики W больше критического значения.

Для проверки гипотезы H₀ против альтернативной H₁: F_x(x) < F_y(y) нужно найти нижнее критическое значение статистики W. В силу симметрии статистики W нижнее критическое значение:

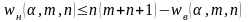
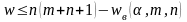
В этом случае гипотеза H₀ должна быть отвергнута, если:

Если альтернативной гипотезой является гипотеза H₁ : F_x(x) ≠ F_y(y), то гипотеза H₀ отвергается, когда:

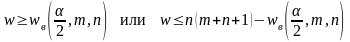
На практике часто приходиться сталкиваться с ситуацией, когда объемы выборок выходят за значения, приведенные в таблицах.

В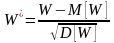 этом случае используют аппроксимацию распределения статистики W. Доказано, что при справедливости гипотезы H₀ при больших m и n случайная величина

распределена по нормальному закону с нулевым математическим ожиданием и единичной дисперсией.

Среднее значение и дисперсия статистики W вычисляются по выражениям:

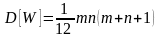
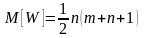
Гипотеза H₀ отвергается с уровнем значимости α

• против альтернативы F_x(x) > F_y(y), если рассчитанное значение W* ≥ Z_α,

• против альтернативы F_x(x) < F_y(y), если W* ≤ -Z_α,

• и против альтернативы F_x(x) ≠ F_y(y), если |W*| ≥ Z_α/2.

Здесь Z_α – квантиль порядка α нормального распределения

На практике в выборке могут иметь место совпадающие значения. Применение критерия Вилкоксона к таким данным приводит к приближенным выводам, точность которых тем ниже, чем больше совпадающих значений. В таких случаях при переходе к рангам группе совпадающих значений присваиваются средние ранги. После этого применяются описанные ранее процедуры.

19. Непараметрический критерий Вилкоксона для проверки однородности двух зависимых выборок

Критерий Вилкоксона для парных выборочных наблюдений основан на рангах разностей между значениями наблюдений в паре. Он используется для проверки гипотезы об однородности наблюдений внутри каждой пары случайных величин (x₁, y₁ ),…, (x_n, y_n), образующих двумерную выборку объема n, при этом пары являются независимыми.

Порядок применения критерия следующий:

1. Вычисляются абсолютные разности наблюдений в паре:

2. Осуществляется ранжирование этих разностей в порядке возрастания и каждому значению ранга присваивается знак его разности.

3. Вычисляется сумма значений рангов, которая образует статистику T.

4. Проверяется, принадлежит ли вычисленное значение T критической области, границы которой находятся по таблицам процентных точек распределения Вилкоксона для парных выборок.

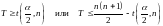
Если вычисленное значение статистики T

то гипотеза об однородности двух выборок отклоняется при уровне значимости α в пользу альтернативной гипотезы H₁: выборки неоднородны.

При альтернативной гипотезе H₁: распределение разности смещено вправо относительно нуля, гипотеза об однородности отклоняется, если вычисленное значение статистики T превышает критическое значение

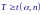
При больших объемах выборки при справедливости нулевой гипотезы статистика

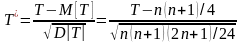
имеет асимптотически нормальное распределение с нулевым математическим ожиданием и единичной дисперсией.

При использование рассматриваемого критерия Вилкоксона нулевые разности игнорируются, при этом объем выборки n в формулах следует уменьшить.

П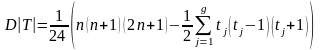 ри использовании статистики T*, если имеются совпадающие значения разностей, то следует заменить D[T] на

здесь g – число связок, t₁,…, t_g – размеры связок.

20. Проверка однородности двух выборок с помощью критерия c²

В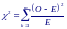 о многих случаях данные получаемые в результате эксперимента, представляют собой число объектов. Выборки, образуемые данными такого рода, можно проверять на однородность с помощью критерия c².

здесь O – обозначает наблюдаемое число событий (например забракованных изделий, зарегистрированных частиц, заболевших людей, правильных ответов и т. д.), E – математическое ожидание числа этих событий.

21. Критерий Стьюдента во множественных сравнениях

Использование критерия Стьюдента для оценки различии большего числа групп посредством их попарного сравнения неприемлем, поскольку при этом вступает в силу эффект множественных сравнений.

Рассмотрим пример. Необходимо исследовать влияние медицинских препаратов на уровень глюкозы в крови. Исследование проводят на трех группах: получавших препарат А, получавших препарат Б и получавших плацебо В. С помощью критерия Стьюдента проводят 3 парных сравнения: группу А сравнивают с группой В, группу Б ― с группой В и наконец А с Б. Получив достаточно высокое значение t в каком либо из трех сравнении сообщают что вероятность ошибочного заключения о существовании различии не превышает 5%. Но это неверно: вероятность ошибки значительно превышает 5%.

В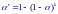 исследовании был принят уровень значимости α = 5% . Значит вероятность ошибиться при сравнении групп А и В ― 5%. Казалось бы все правильно. Но точно также мы ошибемся в 5% случаев при сравнении групп Б и В. И наконец при сравнении групп А и Б ошибка возможна также в 5% случаев. Следовательно, вероятность ошибиться хотя бы в одном из трех сравнении составит не 5%, а значительно больше. В общем случае эта вероятность равна:

где k ― число сравнений.

Значение критерия Стьюдента для Плацебо - Препарат А: 2.39

Значение критерия Стьюдента для Плацебо - Препарат Б: 0.93

Значение критерия Стьюдента для Препарат А - Препарат Б: 1.34

При 5% уровне значимости и числе степеней свободы 10+10 - 2 = 18 критическое значение статистики Стьюдента равно 2,101.

Таким образом при использовании статистики Стьюдента для множественных сравнений пришлось бы заключить, что препарат А оказывает влияние на уровень глюкозы в крови, а препарат Б нет. Но при этом различие в препарате А и Б не наблюдается.