Анализ множественных связей

Оценка степени тесноты связи между входной переменной Y и входными переменными X₁, X₂, ..., X_p, осуществляется с помощью множественного коэффициента корреляции R_y.

Величина R_y² показывает, какая доля от полной дисперсии D[Y] результирующей переменой Y определяется контролируемым нами изменением функции φ(X₁, X₂, ..., X_p):

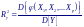
З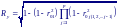 начение множественного коэффициента корреляции R_y можно вычислить, используя частные коэффициенты корреляции, следующим образом:

Для проверки нулевой гипотезы H₀: R_y² = 0 используют статистику:

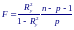
которая при справедливости гипотезы H₀ имеет распределение Фишера с р и n−p−1 степенями свободы. Гипотеза об отсутствии множественной корреляционной связи между Y и X отвергается с уровнем значимости α, если расчетное значение статистики F превышает α-процентную точку распределения Фишера р и n−p−1 степенями свободы.

39. Ранговые коэффициенты корреляции

Если необходимо исследовать двумерные данные, закон распределения которых заметно отличается от нормального, то для решения вопроса о некоррелированности или коррелированности этих данных нельзя применять критерии проверки гипотез о значимости коэффициента корреляции, рассмотренные ранее. В этом случае можно воспользоваться методом, основанным на рангах наблюдений каждой переменной и приводящим к коэффициентам ранговой корреляции.

Коэффициент ранговой корреляции Спирмена

Коэффициент ранговой корреляции Спирмена r_s для выборки (x₁, y₁), ..., (x_n, y_n) объема n определяется как обычный коэффициент корреляции для ранговых переменных. Это означает, что значения X ранжируются по возрастанию и им приписываются ранги от 1 до n. Аналогичная операция осуществляется и с Y. Затем вычисляется коэффициент корреляции между рангами элемента пары (x_i, y_i), i = 1, ..., n.

Т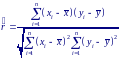 . е., в выражение для выборочного коэффициента корреляции

следует вместо значений выборки подставить их ранги.

Учитывая, что x_i упорядочены в порядке возрастания, ранг x_i равен i (при отсутствии совпадений между x_i). Ранг y_i обозначим через R_i. Поскольку ранги x_i принимают значения от 1 до n, их сумма, как сумма чисел натурального ряда, равна n(n + 1)/2. Отсюда среднее значение рангов x_i

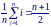
Такое же среднее значение имеют и ранги y_i.

Для коэффициента ранговой корреляции получим выражение:

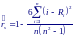
Если два и более значений в исходных данных совпадают, то им присваивают ранг, равный среднему рангов, присваиваемых при отсутствии совпадения.

Закон распределения коэффициента r_s при условии некоррелированности переменных симметричен относительно нуля. Имеются таблицы процентных точек распределения r_s, позволяющие проверять гипотезу о значимости коэффициента ранговой корреляции H₀: r_s=0.

В случае больших выборок (n ≥ 30) для проверки нулевой гипотезы может использоваться статистика

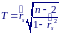
которая распределена по закону Стьюдента с n−2 степенями свободы.

Коэффициент ранговой корреляции Кендалла

Для вычисления коэффициента ранговой корреляции Кендалла r_k необходимо ранжировать данные по одному из признаков в порядке возрастания и определить соответствующие ранги по второму признаку. Затем для каждого ранга второго признака определяется число последующих рангов, больших по величине, чем взятый ранг, и находится сумма этих чисел.

Коэффициент ранговой корреляции Кендалла определяется формулой

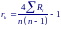
где R_i – количество рангов второй переменной, начиная с i+1, величина которых больше чем величина i-ого ранга этой переменной.

Существуют таблицы процентных точек распределения коэффициента r_k, позволяющие проверить гипотезу о значимости коэффициента корреляции.

П ри больших объемах выборки критические значения r_k не табулируются, и их приходится вычислять по приближенным формулам, которые основаны на том, что при нулевой гипотезе H₀: r_k=0 и больших n случайная величина

распределена приближенно по стандартному нормальному закону.