51. Сравнение двух линий регрессии путем сравнения параметров регрессионной модели

Часто требуется сравнить линии регрессии, рассчитанные по двум выборкам. Это можно сделать тремя способами:

• Сравнить коэффициенты наклона b

• Сравнить коэффициенты сдвига a

• Сравнить линии в целом

Е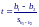 сли нужно проверить, значимо ли различие в наклоне двух прямых регрессии, критерий Стьюдента t вычисляется по формуле:

где b₁–b₂ — разность коэффициентов наклона, a s_b1–b2 — ее стандартная ошибка.

Затем вычисленное значение t сравнивают, с критическим значением, имеющим n₁+n₂–4 степени свободы.

Если обе регрессии оценены по одинаковому числу наблюдений, то стандартная ошибка разности

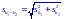
Если же объемы выборок различны, следует воспользоваться объединенной оценкой остаточной дисперсии

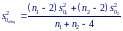
Тогда стандартная ошибка разности

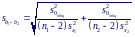
А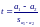 налогично сравниваются и коэффициенты сдвига a₁ и а₂. В этом случае

где a₁–a₂ — разность коэффициентов сдвига, a s_a1–a2 — стандартная ошибка разности коэффициентов сдвига

Затем вычисленное значение t сравнивают, с критическим значением, имеющим n₁+n₂–4 степени свободы.

Сравнить две линии регрессии — значит оценить вероятность нулевой гипотезы о совпадении линий.

Коэффициенты регрессии вычисляются так, чтобы разброс точек вокруг линии регрессии был минимален. Разброс этот характеризуется остаточной дисперсией s₀²: чем меньше остаточная дисперсия, тем лучше прямая регрессии соответствует имеющимся точкам. Следовательно объединив обе выборки в одну и построим для нее линию регрессии получим: в случае если линии регрессии для двух выборок близки, остаточная дисперсия при этом существенно не изменится. И наоборот, если они различаются, то совпадение точек и линии ухудшится и остаточная дисперсия возрастет.

Таким образом порядок сравнения двух линии регрессии:

• Построить прямую регрессии для каждой из выборок.

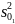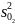• По остаточным дисперсиям и каждой из регрессий вычислить объединенную оценку остаточной дисперсии

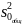
• Объединить обе выборки. Построить прямую регрессии для получившейся выборки и вычислить остаточную дисперсию

Вычислить «выигрыш» от использования двух раздельных регрессий. Мерой выигрыша служит величина:

П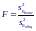 о 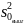и вычислить критерий F:

Сравнить вычисленное значение с критическим значением F для числа степеней свободы 2 и n₁+n₂–4. Если полученное значение больше критического, то гипотеза о совпадении линий регрессии должна быть отклонена.

52. Сравнение двух линий регрессии в целом

53. Линия регрессии, проходящая через начало координат или другую фиксированную точку

П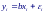 редположим, что еще в начале исследования известно, что прямая регрессии должна пройти через начало координат, т. е. модель регрессии имеет вид

В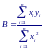 этом случае на основе n имеющихся наблюдений получается следующая оценка единственного параметра b (обозначим ее через B):

Н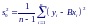 есмещенной оценкой для σ² будет

Выражения для (1 − α) доверительного интервала для значения параметра b имеет вид:

Вычисления по проверки значимости регрессии с помощью дисперсионного анализа проводят следующим образом

Е сли ошибки ε_i распределены по нормальному закону, то при справедливости гипотезы Н₀: b = 0 статистика

распределена по закону Фишера с числом степеней свободы 1 и n−2.

Нулевая гипотеза будет отклонена на уровне значимости α, если вычисленное значение статистики F будет больше α-процентной точки f_1;n−2;α распределения Фишера.

И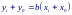 ногда априори известно, что прямая регрессии должна пройти через заданную точку на плоскости (x₀, y₀ ). Наиболее простой способ построения прямой в этом случае заключается в том, чтобы из каждого значения x вычесть x₀, а из каждого y вычесть y₀ и проделать выше описанную процедуру для линии регрессии проходящей через начало координат.

Подогнанная прямая имеет следующий вид: