42. Метод наименьших квадратов

Пусть множество точек (x_i, y_i), i = 1,…, n расположено на плоскости вдоль некоторой прямой

Т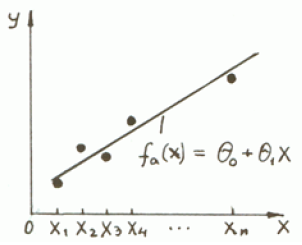 огда в качестве функции f_a(x), аппроксимирующей функцию регрессии f(x) = M [Y|x] естественно взять линейную функцию аргумента x:

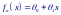
Т. е. в качестве базисных функций здесь выбраны ψ₀(x)≡1 и ψ₁(x)≡x. Такую регрессию называют простой линейной регрессией.

Если множество точек (x_i, y_i), i = 1,…, n расположено вдоль некоторой кривой, то в качестве f_a(x) естественно попробовать выбрать семейство парабол

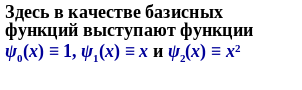
Эта функция является нелинейной по параметрам θ₀ и θ₁, однако путем функционального преобразования (в данном случае логарифмирования) ее можно привести к новой функции f’_a(x) , линейной по параметрам:

43. Простая линейная регрессия

Простейшей моделью регрессии является простая (одномерная, однофакторная, парная) линейная модель, имеющая следующий вид:

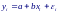
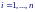
где ε_i – некоррелированные между собой случайные величины (ошибки), имеющие нулевые математические ожидания и одинаковые дисперсии σ², a и b – постоянные коэффициенты (параметры), которые необходимо оценить по измеренным значениям отклика y_i.

Для нахождения оценок параметров a и b линейной регрессии, определяющих наиболее удовлетворяющую экспериментальным данным прямую линию:

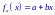
применяется метод наименьших квадратов.

С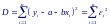 огласно методу наименьших квадратов оценки параметров a и b находят из условия минимизации суммы квадратов отклонений значений y_i по вертикали от “истинной” линии регрессии:

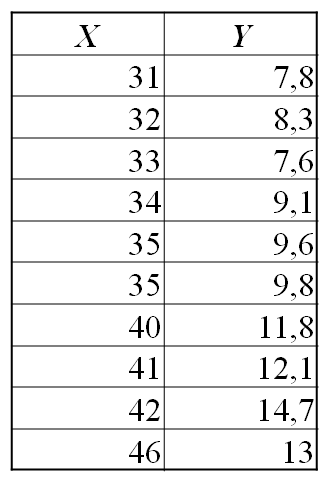
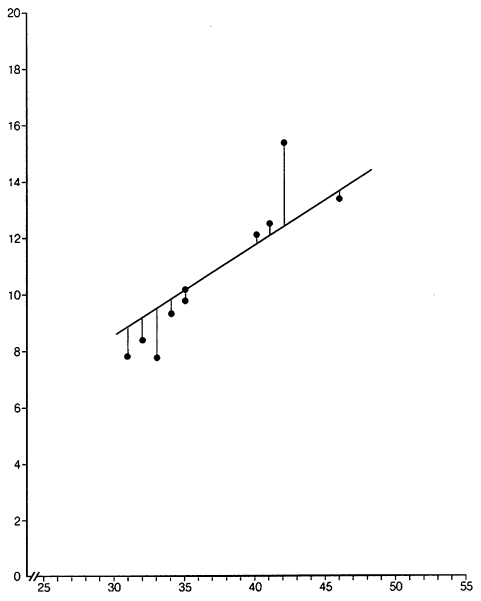
Пусть было произведено десять наблюдений случайной величины Y при фиксированных значениях переменной X

Для минимизации D приравняем к нулю частные производные по a и b:

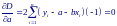
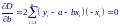
В результате получим следующую систему уравнений для нахождения оценок a и b:

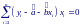
Решение этих двух уравнений дает:

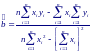
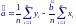
Выражения для оценок параметров a и b можно представить также в виде:

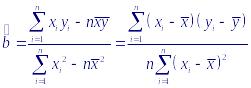
Тогда эмпирическое уравнение регрессионной прямой Y на X можно записать в виде:

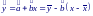
Н есмещенная оценка дисперсии σ² отклонений значений y_i oт подобранной прямой линии регрессии дается выражением

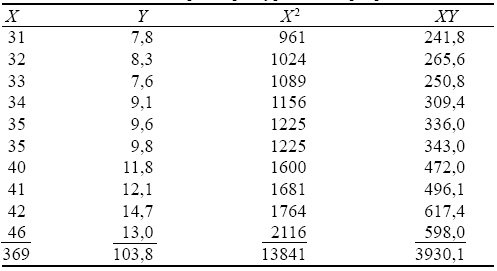
Рассчитаем параметры уравнения регрессии

Таким образом, прямая регрессии имеет вид:

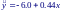
А оценка дисперсии отклонений значений y_i oт подобранной прямой линии регрессии

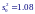
44. Проверка значимости линии регрессии

Найденная оценка b ≠ 0 может быть реализацией случайной величины, математическое ожидание которой равно нулю, т. е. может оказаться, что никакой регрессионной зависимости на самом деле нет.

Чтобы разобраться с этой ситуацией, следует проверить гипотезу Н₀: b = 0 при конкурирующей гипотезе Н₁: b ≠ 0.

Проверку значимости линии регрессии можно провести с помощью дисперсионного анализа.

Р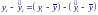 ассмотрим следующее тождество:

Величина y_i − ŷ_i = ε_i называется остатком и представляет собой разность между двумя величинами:

• отклонением наблюдаемого значения (отклика) от общего среднего откликов;

• отклонением предсказанного значения отклика ŷ_i от того же среднего

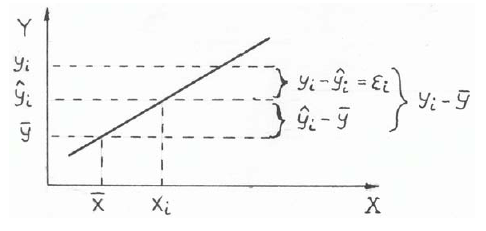
Записанное тождество можно записать в виде

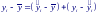
Возведя обе его части в квадрат и просуммировав по i, получим:

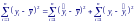
Г де величины получили название:

полной (общей) суммой квадратов СК_п, которая равна сумме квадратов отклонений наблюдений относительно среднего значения наблюдений

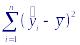
сумма квадратов, обусловленной регрессией СК_р, которая равна сумме квадратов отклонений значений линии регрессии относительно среднего наблюдений.

о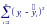 статочная сумма квадратов СК₀. которая равна сумме квадратов отклонений наблюдений относительно значений линии регрессии

Таким образом, разброс Y-ков относительно их среднего значения можно приписать в некоторой степени тому факту, что не все наблюдения лежат на линии регрессии. Если бы это было так, то сумма квадратов относительно регрессии была бы равна нулю. Отсюда следует, что регрессия будет значимой, если сумма квадратов СК_р будет больше суммы квадратов СК₀.

Вычисления по проверки значимости регрессии проводят в следующей таблице дисперсионного анализа

Если ошибки ε_i распределены по нормальному закону, то при справедливости гипотезы Н₀: b = 0 статистика:

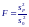
распределена по закону Фишера с числом степеней свободы 1 и n−2.

Нулевая гипотеза будет отклонена на уровне значимости α, если вычисленное значение статистики F будет больше α-процентной точки f_1;n−2;α распределения Фишера.