54. Обратная простая регрессия

В основе построения градировочных графиков, как правило, лежат методы линейной регрессии. Трудность построения и использования градуировок связана с так называемой проблемой обратной регрессии. Дело в том, что зависимая и независимая переменные меняются местами при использовании готового графика. То, что было независимой переменной, при измерении становится результатом, что порождает существенные проблемы.

Предположим, что необходимо провести калибровку манометра (датчика давления) и при этом известно, что показания манометра являются линейной функцией давления:

Ч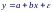 то можно записать в виде уравнения:

Для калибровки манометра на него подают n контролируемых давлений x_i (i = 1, 2,…, n) и считывают показания манометра y_i. По этим данным подбирают уравнение

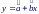
к оторое можно использовать для оценивания (предсказания) неизвестного давления x₀ при заданном показании манометра y₀

В то же время для x₀ можно рассчитать границы (1 − α) доверительного интервала:

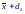
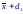
где d₁ и d₂ – действительные несовпадающие корни уравнения:

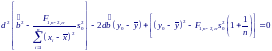
Конечный доверительный интервал получается тогда и только тогда, когда

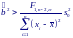
т . е. когда регрессия является значимой.

Если оценка x₀ не попадает в границы интервала и , то доверительная область для x₀ состоит их двух полупрямых.

Если же уравнение не имеет действительных корней, то доверительная область совпадает во всей действительной прямой.

55. Множественная линейная регрессия

Во многих практических задачах простая (однофакторная) линейная регрессия дает недостаточную информацию о зависимой переменной. Так, например, урожайность какой-либо культуры определяется несколькими факторами, такими как количество осадков, температура, влажность воздуха, физические и химические показатели почвы и т. д. В таких случаях обращаются к множественной регрессионной модели.

М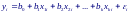 одель множественной линейной регрессии имеет следующий вид:

Предположения относительно множественной линейной регрессии аналогичны тем, которые применялись для простой линейной регрессии. В частности, что все x_i считаются фиксированными и для любого набора x_i значения y_i распределены по нормальному закону с постоянной дисперсией.

Д ля получения оценок параметров b₀, b₁, ...,b_k методом наименьших квадратов нужно минимизировать по этим параметрам выражение

П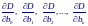 риравняв нулю частные производные

после упрощений получается следующая система нормальных уравнений для нахождения оценок параметров:

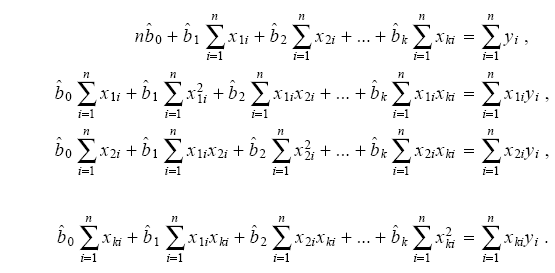
Пусть b – вектор-столбец размера (k+ 1), состоящий из коэффициентов b₀ , b₁, …, b_k , y – вектор-столбец из n наблюдений, ε – вектор-столбец из n ошибок и X – матрица наблюдений размером n(k+ 1) :

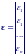
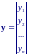
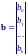
Тогда уравнение модели регрессии можно записать в виде:

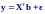
Выражение для D можно представить в матричном виде:

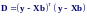
тогда вектор оценок b получается из решения системы уравнений:

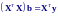
решение которой имеет вид:

Н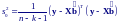 есмещенной оценкой дисперсии является:

Дисперсионный анализ множественной линейной регрессии проводится в следующей таблице: