48. Доверительные интервалы для параметров простой линейной регрессии

Подобно тому как выборочное среднее - это оценка истинного среднего (среднего по совокупности), так и выборочные параметры уравнения регрессии a и b - не более чем оценки истинных коэффициентов регрессии. Разные выборки дают разные оценки среднего — точно так же разные выборки будут давать разные оценки коэффициентов регрессии.

В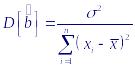 предположении, что закон распределения ошибок ε_i описываются нормальным законом, оценка параметра b будет иметь нормальное распределение с параметрами:

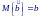
П оскольку оценка параметра a представляет собой линейную комбинацию независимых нормально распределенных величин, она также будет иметь нормальное распределение с математическим ожиданием и дисперсией:

При этом (1 − α) доверительный интервал для оценки дисперсии σ² с учетом того, что отношение (n−2)s₀²/σ² распределено по закону χ² с числом степеней свободы n−2 будет определяться выражением

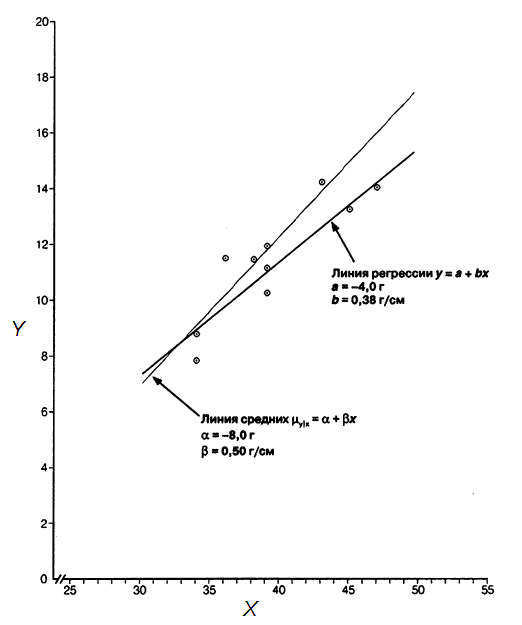
49. Доверительные интервалы для линии регрессии. Доверительный интервал для значений зависимой переменной

Обычно мы не знаем истинных величин коэффициентов регрессии а и b. Нам известны только их оценки. Иначе говоря, истинная прямая регрессии может пройти выше или ниже, быть более крутой или пологой, чем построенная по выборочным данным. Мы вычислили доверительные интервалы для коэффициентов регрессии. Можно вычислить доверительную область и для самой линии регрессии.

П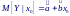 усть для простой линейной регрессии нужно построить (1−α) доверительный интервал для математического ожидания отклика Y при значении х = х₀. Это математическое ожидание равно a+bх₀, а его оценка

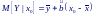
Поскольку , то .

П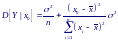 олученная оценка математического ожидания представляет собой линейную комбинацию некоррелированных нормально распределенных величин и поэтому тоже имеет нормальное распределение с центром в точке истинного значения условного математического ожидания и дисперсией

Поэтому доверительный интервал для линии регрессии при каждом значении x₀ можно представить в виде

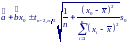
Как видно минимальный доверительный интервал получается при x₀ равному среднему значению и возрастает по мере того, как x₀ “удаляется” от среднего в любом направлении.

Д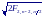 ля получения множества совместных доверительных интервалов, пригодных для всей функции регрессии, на всем ее протяжении, в приведенное выше выражении вместо t_n−2,α/2 необходимо подставить

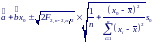
Доверительный интервал для значений зависимой переменной

Р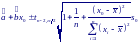 азброс значений складывается из разброса значений вокруг линии регрессии и неопределенности положения самой этой линии. Характеристикой разброса значений вокруг линии регрессии является оценка дисперсии s₀², а неопределенности положения линии регрессии дисперсия D[Y|x₀]. Дисперсия суммы двух величин равна сумме дисперсий D[Y] =D[Y|x₀]+s₀², поэтому доверительный интервал для индивидуального значения Y₀ будет иметь вид

50. Проверка гипотез относительно параметров линейной регрессии

Рассмотрим критерии проверки гипотез относительно параметров a, b и 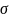².

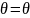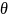Заметим, что проверку некоторых гипотез можно связать с построением доверительных интервалов. Пусть, например, проверяется гипотеза H0 : ₀ с уровнем значимости, скажем 0.01, при альтернативной гипотезе H1: ≠ ₀. Тогда можно построить 0.99 доверительный интервал для параметра . Если он накрывает параметр ₀, то гипотеза H0 принимается, в противном случае – отклоняется.

Для проверки гипотезы H0 : b=b₀ против H1 : b ≠ b₀ используется статистика

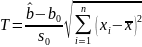
которая при справедливости нулевой гипотезы имеет распределение Стьюдента с n − 2 степенями свободы. Если расчетное значение статистики Т 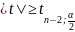то гипотеза отвергается.