33. Корреляционный анализ. Постановка задач статистического исследования зависимостей

В математическом анализе зависимость между величинами x и y выражается функцией y = f(x), где каждому значению x соответствует одно и только одно значение y. Такая связь называется функциональной.

Для случайных величин X и Y такую зависимость можно установить не всегда. Связь между случайными величинами является не функциональной, а случайной (стохастической), при которой изменение переменной X влияет на значения переменной Y через изменение закона распределения случайной величины Y.

Таким образом задача корреляционного анализа исследование наличия взаимосвязей между отдельными группами переменных и установление тесноты (силы) связи между ними.

Порядок проведения корреляционного анализа как правило включает:

• выбор показателя статистической связи анализируемых переменных

• оценка значения этого показателя по имеющимся экспериментальным данным, т. е. нахождение его точечной и интервальной оценки

• проверка статистической гипотезы о том, что значение показателя статистической связи значимо отличается от нуля

34. Измерители парной статистической связи. Корреляционное отношение

П ри функциональных преобразованиях случайных величин вида Y = ϕ(X) для нахождения математического ожидания и дисперсии случайной величины Y достаточно знать закон распределения случайной величины X:

В процессе наблюдения величины Y = ϕ(X) для каждого фиксированного значения x′ случайной величины X можно иметь разброс значений Y, обусловленный погрешностями прибора или какими-либо неконтролируемыми факторами, и можно вычислить величину дисперсии

Тогда суммарная дисперсия случайной величины Y = ϕ(X) будет состоять из двух слагаемых:

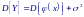
П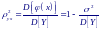 ервое слагаемое обусловливает вклад в дисперсию от функциональной зависимости Y = ϕ(X), а второе – случайный разброс вокруг математического ожидания M[ϕ(X)]. Введем понятие квадрата корреляционного отношения

которое показывает долю дисперсии, обусловленную чисто функциональной связью ϕ(X), в полной дисперсии случайной величины Y. Это наиболее общая характеристика степени тесноты связи между случайными величинами Y и X.

Очевидно, что 0 ≤ ρ²_yx ≤ 1. Стремление ρ²_yx к нулю означает, что доля дисперсии, обусловленная функциональной связью, очень мала. Наоборот, стремление ρ²_yx к единице показывает, что случайными изменениями Y можно пренебречь и вся дисперсия обусловлена функциональной зависимостью Y = ϕ(X).

Аналогично определяется квадрат корреляционного отношения ρ²_xy переменной X по Y. Однако между ρ²_yx и ρ²_xy нет какой-либо простой зависимости.

Положительный корень из ρ²_yx носит название корреляционного отношения, которое является показателем статистической связи между двумя случайными величинами X и Y для самой общей ситуации, когда закон распределения системы (X,Y) является произвольным.

35. Коэффициент корреляции как измеритель степени тесноты связи

Рассмотрим двумерную нормальную совокупность, плотность вероятности которой имеет вид

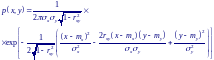
где r_xy – коэффициент корреляции между случайными величинами Y и X.

Для условной плотности вероятности случайной величины Y (плотности при условии, что случайная величина X приняла определенное значение X = x) получим:

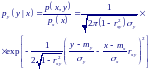
Отсюда видно, что условная плотность вероятности случайной величины Y тоже имеет нормальное распределение с математическим ожиданием

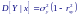
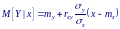
и дисперсией

характеризующей разброс случайной величины Y вокруг математического ожидания.

Тогда для квадрата корреляционного отношения получаем

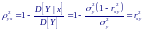
т. е. корреляционное отношение для двумерного нормального распределения совпадает с коэффициентом корреляции.

Аналогично можно показать, что ρ²_xy= r²_yx, откуда, поскольку r²_xy= r²_yx, для нормально распределенных величин ρ²_xy= ρ²_yx=r².

К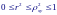 оэффициент корреляции являются измерителям степени тесноты линейной статистической связи между случайными величинами. Формально его можно вычислить для любой двумерной системы случайных величин, однако только для совместной нормальной совокупности коэффициент корреляции имеет четкий смысл как характеристика тесноты связи.

В общем случае показатели ρ²_xy и r² связаны неравенствами

При этом возможны следующие варианты:

• r² = ρ²_yx=1 только тогда, когда имеется строгая линейная функциональная зависимость Y от X

• r² < ρ²_yx=1 только тогда, когда имеется строгая нелинейная функциональная зависимость Y от X

• r² = ρ²_yx<1 только тогда, когда зависимость Y от X строго линейна, но нет функциональной зависимости

• r² < ρ²_yx<1 указывает на то, что не существует функциональной зависимости, а некоторая нелинейная кривая “подходит” лучше, чем “наилучшая” прямая линия.

Таким образом, в качестве показателя статистической связи между двумя случайными количественными переменными X и Y следует выбрать корреляционное отношение ρ_yx (или ρ_xy) , если закон распределения системы (X,Y) вызывает сомнение. Если же можно с большой степенью уверенности считать закон распределения системы (X,Y) нормальным, то вместо корреляционного отношения следует использовать коэффициент корреляции r.