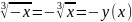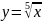- •1. Цели и задачи изучения курса алгебры, алгебры и начал анализа в 9-11 классах
- •2. Понятие функции в мат-ке и в школьном курсе мат-ки. Формирование понятия функции в школьном курсе мат-ки
- •3. Знания и умения школьников, связанные с понятием функции. Методика введения понятия функции
- •4. Методика изучения линейной функции
- •5. Методика изучения квадратичной функции
- •6. Методика изучения общих свойств функции
- •7. Расширение понятия степени. Методика введения понятия степени с целым показателем
- •8. Методика введения арифметического корня с натуральным показателем, степени с рациональным показателем
- •9. Определение степени с действительным показателем и её свойства
- •10. Теоретические основы изучения степенной функции
- •11.Урок обобщения и систематизации по теме «Степенная ф-ция»
- •12.Проект изучения темы «Арифметическая и геометрическая прогрессии» (9 класс). Урок решения ключевых задач (метод уде)
- •Глава 4, §§14-16.
- •Глава 4, §§14-16.
- •Ход урока
- •12. Теор. Основы изучения темы «Арифметическая и геометрическая прогрессии»
- •13. Методика изучения показательной функции
- •14. Теоретические основы изучения логарифмической функции. Методика введения понятия логарифма
- •1. Мотивационно-ориентировочный этап
- •2. Содержательный этап.
- •15. Разработка урока-лекции «Логарифмическая функция, её свойства и график»
- •I. Мотивационно-ориентировочная часть.
- •II.Содержательная часть.
- •16. Методические основы введения и изучения элементов тригонометрии: числовая окружность, числовая окружность на координатной плоскости
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •18. Теоретические основы изучения темы «Тождественные преобразования тригонометрических выражений». Урок решения ключевых задач
- •19. Методические рекомендации к изучению тригонометрических функций. Методика изучения свойства периодичности функции
- •21. Проект урока-лекции «Решение уравнений и неравенств Арксинус числа. Свойства арксинуса числа»
- •22. Проект урока-лекции «Решение уравнений и неравенств Арккосинус числа. Свойства арккосинуса числа»
- •23. Проект урока-лекции «Решение уравнений и неравенств Арктангенс числа. Свойства арктангенса числа»
- •24. Методика обучения решению триг. Уравнений и неравенств. Основные приёмы решения триг. Уравнений
- •Семинар-практикум по теме: «Основные приёмы решений тригонометрических уравнений».
- •25. Логические основы решения уравнений и неравенств в старших классах. Методические рекомендации к изучению понятий равносильные уравнения, уравнения – следствия, теорем о равносильности уравнений
- •26. Методика обучения учащихся решению частных видов уравнений и неравенств. Построение урока решения задач (на примере темы «Логарифмические уравнения и неравенства»)
- •2.Операционно-познавательный этап.
- •1. Решите уравнение:
- •2) Решите уравнение: .
- •3) Решите уравнение:
- •4) Решите уравнение: .
- •6) Решить неравенство: .
- •3.Рефлексивно-оценочный этап.
- •27. Организация заключительного повторения в 11 классе темы «Уравнения и неравентсва». Урок-лекция «общие методы решения уравнений»
- •1 Группа.
- •2 Группа.
- •3 Группа.
- •28. Методика введения понятий предела функций в точке и непрерывности функции
- •29. Методика введения понятия производной функции
- •30. Методика изучения геометрического смысла производной, уравнения касательной к графику функции
- •31. Теоретические и методические основы изучения темы «Применение производной к исследованию функции»
- •32. Теоретические и методические основы изучения первообразной и интеграла
- •33. Причины включения в школьный курс математики элементов вероятностно-статистической линии. Основные цели изучения элементов теории вероятностей и математической статистики
- •34. Теоретические и методические основы изучения теории вероятностей в школьном курсе математики 9-11 классов
10. Теоретические основы изучения степенной функции
Степенная
функция изучается на протяжении
нескольких лет. Её изучение начинается
в 7 классе – y=x,
в 8 классе
,
в 9 классе впервые вводится термин
«степенная функция» и изучаются функции
вида
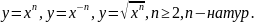 В 10 классе сведения о степенной функции
обобщаются и систематизируются.
В 10 классе сведения о степенной функции
обобщаются и систематизируются.
Ко
времени изучения степенной функции в
9 классе учащиеся знают понятие степени
с рациональным показателем, его свойства,
уточнено понятие функции и рассматриваются
её общие свойства. Нужно решить несколько
практических задач, когда приходят к
функциональным зависимостям вида
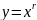 ,
r-фиксированное
число, различное в каждом случае.
,
r-фиксированное
число, различное в каждом случае.
- Итак, имеем функцию вида , где r - рациональное число (в 10 кл – r -действительное число). Такая функция имеет название степенной.
-
Можете ли вы указать степенные функции,
которые уже рассматривали? ( ).
).
- Постройте график каждой из данных функций. Определите их свойств по графику.
- Можно отметить, что у этих функций показатель степени – целое число (у первых двух – натуральное число: у первой нечётное число, а у второй – чётное). То есть свойства и вид графика степенной функции будут зависеть от показателя степени.
- Вспомним, как последовательно определялась рациональная степень (натуральная степень, целая отрицательная, дробная). В такой же последовательности будем рассматривать показатель степенной функции.
Учебная задача: изучить функцию вида , где r - натуральное, отрицательное целое число, затем дробь вида 1/n.
Итак, графики и свойства функций позволили спрогнозировать, что степенную функцию при натуральном показателе следует изучать в 2 случаях: 1 - показатель степени чётное; 2 - нечётное число.
Степенная функция с натуральным показателем.
|
|
а) y = x (график) |
а) (график) |
Свойства: 1. D(y): R 2. Е(у): R 3. возрастает на R 4. нечётная, т.к. у(-х) = -х = -у(х) 5. непрерывная 6. нет ни н/м, ни н/б значения, неограниченная
б)
x 0 1 -1 2 -2 y 0 1 -1 8 -8 Свойства: 1) D(y): R 2) Е(у): R x<0⇒y<0, x=0⇒y=0, x>0⇒y>0 Док-во:
-
Любое ли действительное число x0
является значением данной ф-ции, т.е.
существует ли действительное число
такое, что
3)
возрастает, т.к. при x1<x2,
y(x2)-y(x1)
= 4). нечётн. y(-x) = (-x)3 = -x3 = -y(x) (св-во чт / нчт ф-ции вводится на примере степенной ф-ции) 5). непрерывная (по графику) 6). неограниченная, т.е. не имеет н/б и н/м значений. в) . Обобщаем. |
Свойства: 1. D(y): R 2. Е(у): y ≥ 0
3. x>0 ⇒ возрастает, x<0 ⇒ убывает, Док-во: - 0< x1<x2, то y( x1) < y(x2)
y(x2)
- y(x1)=
- x1<x2<0, то y( x1) > y(x2)
4.
чётная, т.к. y(-x)= 5. непрерывная 6. имеет н/м значение y=0, ограничена снизу. б) , n-натур. Обобщаем. Строим графики y = x2 и y = x4 Обратить внимание учащихся на взаимное расположение графиков. Свойства обобщаются и записываются без док-ва. Свойства: 1. D(y): R 2. Е(у): y ≥ 0
3. x>0 ⇒ возрастает, x<0 ⇒ убывает, 4. чётная, т.к. y(-x)= (по опр-ю) 5. непрерывная 6. имеет н/м значение y=0, ограничена снизу. |
Строим на одном графике функции у = х3, у = х5 Обратить внимание учащихся на тот факт, что графики этих функций периодически меняют своё взаимное расположение. Перечисляются все свойства без док-ва. Свойства: 1. D(y): R 2. Е(у): R 3. возрастает на R 4. нечётная. 5. непрерывная 6. нет ни н/м, ни н/б значения, неограниченная |
|
Далее
рассматриваются функции с целым
отрицательным показателем y
= x-n
или
y
=
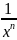 ,
,
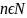 .
Можно организовать семинарское занятие
по изучению этой темы, ученики разбиваются
на группы и сами строят, исследуют
свойства функций.
.
Можно организовать семинарское занятие
по изучению этой темы, ученики разбиваются
на группы и сами строят, исследуют
свойства функций.
1)
 2)
2)
 ,
,
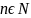
От чётности степени зависят свойства функции.
И
наконец, функция вида
 ,
n
,
n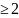 .
Основные свойства таких функций тоже
не доказываются. Строятся графики по
точкам, и дальше идёт исследование по
графикам.
.
Основные свойства таких функций тоже
не доказываются. Строятся графики по
точкам, и дальше идёт исследование по
графикам.
а)
Свойства: 1. D(y):
2.
Е(у): y
3.
Возрастает 0<x1<x2
⇒
4. Функция общего вида 5. Непрерывна 6. Имеет н/м значение, ограничена снизу, у = 0.
б)
Строят
графики
Свойства обобщаются. Обратить внимание на взаимн. расположение. |
б)
Св-ва: 1. D(y): R 2. Е(у): R 3. Возрастает на R
4.
Нечётная, т.к. y(-x)
=
5. Непрерывная 6. Неограниченная, не имеет н/б и н/м значений
б)
Строят
графики
и
Свойства обобщаются. |
В 10 классе все сведения по степенной функции нужно обобщить и систематизировать. В учебнике рассматриваются свойства функции y=xp в зависимости от p:
1. Показатель p = 2n – чётное натур-ое число
2. Показатель p = 2n-1 – нечётное натур-е число
3. Показатель p = -2n, где n – натур-е число
- D(y): R\0
- Е(у): y > 0
- чётная
- возрастает на промежутке x < 0, убывает на x > 0.
4. Показатель p = -(2n-1), где n - натур-е число
- D(y): R\0
- Е(у): R\0
- нечётная
- убывает на промежутках x > 0и x < 0.
5. Показатель p – положительное действительное нецелое число
6. Показатель p – отрицательное действительное нецелое число
- D(y): x > 0
- Е(у): y > 0
- убывающая на промежутке x > 0.

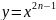 ,
n-натур
,
n-натур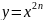 ,
n-натур
,
n-натур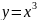 (график)
(график)
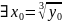 (по определению корня нечётной степени)
такое, что
(по определению корня нечётной степени)
такое, что
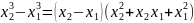 >0, значит y(x2)
> y(x1)
>0, значит y(x2)
> y(x1)
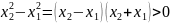 => y( x1)
< y(x2)
=> y( x1)
< y(x2) =>y(
x1)
>y(x2)
=>y(
x1)
>y(x2)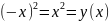 (по опр-ю)
(по опр-ю)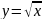 (график).
(график).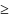 0
0
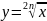 ,
,
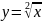 и
и
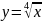
 (график)
(график)