5. Методика изучения квадратичной функции

Необходимо вначале провести актуализацию, т.е. вспомнить понятие функции, как изучалась линейная функция.

Опр. Если каждому значению х из некоторого множества Х поставлено в соответствие число у, то говорят, что на этом множестве задана функция у(х), при том х называют независимой переменной (аргументом), а у – зависимой переменной (функцией). (В учебнике Ш.А. Алимова и др.)

Опр. Линейной функцией называется функция y = kx + b, где k и b – заданные числа.

График функции y = kx + b получается из графика функции y = kx сдвигом вдоль оси ординат на |b| вверх, если b>0; вниз, если b<0. Графики функций y = kx + b и y = kx – параллельные прямые.

Далее идёт мотивация.

Задача 1. Одна из сторон прямоугольника на з см больше другой стороны, найдите его площадь.

Решение: S = x(x+3) = x²+3x. Получили функцию S(x) = x²+3x, где х - независимая, S – зависимая.

Задача 2. Тело брошено в верх с высоты 24 м со скоростью 2м/с. На каком расстоянии от поверхности Земли будет находиться тело в момент времени t?

Решение: S = -gt²/2 + V₀t + S₀, где V₀ = 2м/с, S₀ = 24м, g = 9,8м/с²

Тогда S = -4,9t² + 2t + 24, где t – независимая переменная, S – зависимая.

И в том и в другом примере имеем дело с функцией нового вида: y = ax² + bx + c, где a ≠ 0.

Формулируется определение квадратной функции.

Опр. Функция y = ax² + bx + c, где a, b и c – заданные действительные числа, a ≠ 0, x – действительная переменная, называется квадратичной функцией.

Затем даются упражнения на узнавание. Решаются задачи трёх ранее указанных типов. При решении задач третьего типа берётся у = 0, тогда найденное значение х называется нулём квадратичной функции. Это понятие вводится впервые и устанавливает связь квадратичной функции с соответствующим квадратным уравнением, его корнями. Затем подробно рассматривается функция у = х², строится её график по 5 пунктам.

Рассмотрим функцию у = х², т.е. квадратичную функцию y = ax² + bx + c при а = 1, b = c = 0. 1). Составим таблицу её значений:

х	-4	-3	-2	-1	0	1	2	3	4
у = х2	16	9	4	1	0	1	4	9	16

2). Построим точки, координаты которых заданы в таблице.

3). Т.к. х – любое число, то проведём через полученные точки сплошную линию.

4) Находим по заданной формуле другие точки. Проверяем принадлежат ли точки с заданными координатами данной прямой.

5). Берём точку на построенной прямой и находим её координаты. Подставляем найденные координаты в формулу и убеждаемся, что равенство верно.

Для построения графика этой функции лучше взять масштаб 1 см. Проходя пункт 3, обязательно подчёркиваем, что х – любое число, поэтому графиком функции является сплошная линия. Учитель сам показывает вид этой линии. После прохождения всех 5 пунктов, учитель говорит: «Кривая, являющаяся графиком функции у = х² называется параболой». Далее рассматриваются её свойства по графику:

1. Значение функции у = х² положительно при х ≠ 0 и равно нулю при х = 0. Следовательно, парабола у = х² проходит через начало координат, а остальные точки параболы лежат выше оси абсцисс. Говорят, что парабола у = х² касается оси абсцисс в точке (0; 0)

2. График функции у = х² симметричен относительно оси ординат, т.к. (-х)² = х². Например, у(-3) = у(3) = 9. Таким образом, ось ординат является осью симметрии параболы. Точку пересечения параболы с её осью симметрии называют вершиной параболы. Для параболы у = х² вершиной является начало координат.

3. При 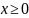большему значению х соответствует большее значение у. Например, у(3) > y(2). Говорят, что функция у = х² является возрастающей на промежутке .

При большему значению х соответствует меньше значение у. Например, у(-2) < y(-4). Говорят, что функция у = х² является убывающей на промежутке .

Затем изучается функция у = ах², при различных а ≠ 0.

Следует провести сравнение с функцией у = х², например, составляя таблицы:

х	0	±1	±1/2	±2
у = х2	0	1	¼	4
у = 2х2	0	2	1/2	8

Значения 2-ой функции в два раза больше, чем 1-ой.

х	0	±1	±1/2	±2
у = х2	0	1	¼	4
у = ½ х2	0	½	1/8	2

Значения 2-ой функции в два раза меньше, чем 1-ой.

Появляется понятие: растяжение (сжатие) вдоль оси Оу. Увеличение приводит к растяжению, уменьшение – к сжатию. Говорят, что график функции у = 2 х² получается растяжением графика функции у = х² от оси Ох вдоль оси Оу. Говорят, что график функции у = ½ х² получается сжатием графика функции у = х² к оси Ох вдоль оси Оу.

х	0	±1	±1/2	±2
у = х2	0	1	1/4	4
у = -х2	0	-1	-1/4	-4

Появляется понятие: отражение от оси, в дано случае от оси Ох. График функции у = -х² можно получить симметрией относительно оси Ох графика функции у = х².

График функции у = ах² при любом а ≠ 0 также называют параболой. При a > 0 ветви параболы направлены вверх, а при a < 0 – вниз. В итоге появляется следующее правило: график функции у = ах² можно получить из графика функции у = х² растяжением вдоль оси Оу в |a| раз, при |a|>1; и сжатием вдоль оси Оу в 1/|a| раз при 0<|a|<1; и отражением от оси Ох, если a<0.

Рассматриваются свойства.

1. Если a > 0, то функция у = ах² принимает положительные значения при х ≠ 0; если a < 0, то функция у = ах² принимает отрицательные значения при х ≠ 0; значение функции у = ах² равно нулю только при х = 0.

2. Парабола у = ах² симметрична относительно оси ординат.

3. Если a > 0, то функция у = ах² возрастает при и убывает при ; если a < 0, то функция у = ах² убывает при и возрастает при .

Выполняются упражнения на построение графиков, их чтение. Решаются простейшие квадратные неравенства графическим методом.

Пример: Решить неравенство 2х² > 8.

Строим графики функций у = 2х² и у = 8. Для того, чтобы решить неравенство, нужно найти те значения х, при которых точки параболы у = 2х² лежат выше прямой у = 8.

По аналогичной схеме устанавливается, что график функции у = х² + b можно получить из графика функции у = х² сдвигом вдоль оси Оу. График функции у=(х + b)² получается из графика функции у = х² сдвигом вдоль оси Ох.

Устанавливаются свойства таких функций:

Те же что и ранее, только 2 пункт: ось симметрии параллельна оси ординат.

Далее рассматривается функция у = 2(х – 1)² + 3. Обсуждается получение её графика из графика функции у = х². Преобразуя выражение получаем функцию у = 2х² – 4х + 5. Таким образом, возникает предположение, что график любой квадратичной функции у = ах² + bx + c, a ≠ 0 может быть получен из графика функции у = х² соответствующими преобразованиями, т.е. является параболой.

Чтобы чётко увидеть преобразования, нужно выделить полный квадрат у функции.

=

.

,

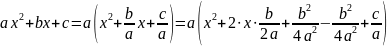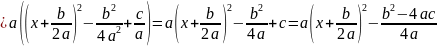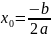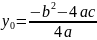
Получаем функцию , где (x₀; y₀) – координаты вершины параболы.

Графиком функции является парабола, получаемая сдвигом параболы у = ах²: вдоль оси абсцисс на х₀, если x₀ > 0, направо на |x₀|, если x₀ < 0; вдоль оси ординат вверх на у₀, если y₀ > 0, вниз на |y₀|, если y₀ < 0.

Устанавливаются свойства квадратичной функции общего вида. На построение графика любой квадратичной функции общего вида далее ведётся по следующей схеме:

1) Вершина параболы. Построить вершину параболы ,вычислив х₀, у₀ по формулам ,

2). Ось симметрии – провести через вершину параболы прямую, параллельную оси ординат.

3). Нули функции, если они есть. И построить на оси абсцисс соответствующие точки параболы.

4). Несколько дополнительных точек симметричных друг другу. Для этого

Необходимо взять две точки на оси Ох, симметричные относительно точки х₀ и вычислить соответствующие значения функции.

5). График. Провести через построенные точки параболу.

Выполняются упражнения на построение графиков, чтение графиков. А именно на нахождение множества значений, н/б или н/м значения, промежутков знакопостоянства, возрастания/убывания функции.

Функция y = ax² + bx + c принимает наименьшее или наибольшее значение в точке , которая является абсциссой вершины параболы. Если a > 0, то функция имеет наименьшее значение, а если а < 0, то функция имеет наибольшее значение.