17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)

В учебнике Алимова рассматривается α как угол, принимающий значения, выражающиеся в градусах ил рад. Затем α рассм-ся как произвол. число.

В учебнике Мордковича посл-сть обратная.

Но независимо от учебника метод. подходы к введению синуса, косинуса, тангенса и котангенса одинаковы.

Следует отметить, что с элементами тригонометрии учащиеся встречались и не однажды. В курсе геометрии 8 класса в теме «Подобные трег-ки» рассм-сь тема «Соотношения между сторонами и углами треуг-ка»Здесь даются определения синуса, косинуса, тангенса острого угла прямоугольного треуг-ка через отношение соот-щих катетов и гипотенузы. Рассм-ся формулы

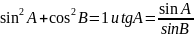
Определяются значения синуса, косинуса, тангенса для углов 30 град, 45 град, 60 град. Далее это находит применение в курсе физики 8 класса.

Второй раз учащиеся встречаются с элементами тригом-ии в 9 классе в курсе геометрии в теме «Соотношения между сторонами и углами треуг-ка». Здесь вводится def единич. полуокр. и синуса, косинуса, тангенса α, где α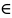 [0, π], синус – ордината, косинус – абсцисса точки единич. полуокр. Но это вводится на основе предыдущих defs: .

Рассм-ся осн. тригоном. тождество, формулы приведения: 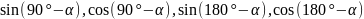. Все это исп-ся для записи формулы площади треуг-ка: половина произведения сторон на синус угла между ними, для записи теоремы косинусов, синусов, для нахождения различных элементов произвольного треуг-ка (решенеи треуг-ка) по трем данным эл-м, определяющим треуг-к, для введения скалярного произведения векторов.

Т. о., происходит пропедевтика к изучению тригонометрии в куре алгебры 9-11 классов.

В 9 кл. в курсе алгебры в теме «Элементы тригонометрии» вводятся понятия синуса, косинуса, тангенса и котангенса числа (у А. Г. Мордковича), угла (у Ш. А. Алимова).

- Вы знаете, что любому числу (углу) α соот-ет !точка числ. окр-ти Pα. Точка Pα имеет две декартовые коор-ты (xα, yα). Абсциссу xα наз. косинусом числа (угла) α, а ординату yα - синусом числа (угла) α. Появляется запись .

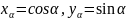Вводятся четкие определения синуса и косинуса через род и видовое отличие.

Синусом угла α наз. ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается sin α).

Косинусом угла α наз. абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (обозначается cos α).

Тангенс и котангенс определяются как отношение формулами.

Тангенсом угла α наз. отношение синуса угла α к его косинусу (обозначается tg α).

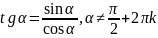
Котангенс угла α (обозначается ctg α)определяется формулой

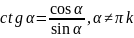
В итоге можно сразу установить, что синус и косинус определены для любого α, а тангенс и котангенс только для определенных.

Далее следует отметить, что defs синуса и косинуса имеют геомет. интерпретацию: ось ординат – это ось синусов, ось абсцисс – это ось косинусов, поэтому целесообразно ввести здесь же геометрич. интерпрет. тангенса и котангенса.

- Пусть дана числ. окр. Проводим прямую l парал-но Оу через точку (1, 0). Она явл-ся касательной к окр-ти в этой точке, т. к. перпенд-на радиусу. Пусть .

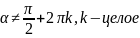- Рассм. точку Pα c корд-ми (cos α, sin α). OPα пересекаем с l. Получаем точку Tα. Найдем ее координаты, обозначив их (x_0, y_0).

- x_0=1

- Уравнение прямой OPα имеет вид y=kx (проходит через (0, 0)). Подставим в него коорд-ты точки Pα, чтобы найти k:

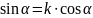
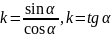
- Точка Tα принадлежит OPα, значит, ее корд-ты удовлетворяют ур-ю:

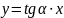
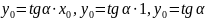
- Итак, длина отрезка ATα равна tgα (|tg α|). Поэтому прямую l наз. осью тангенсов, где точка А считается началом отсчета, т. к. она соот-ет tg0, равному 0.

- tgπ/4=1, поэтому ед. отр. оси тангенсов равен ед. отр. осей корд-т. Положит. направление l совпадает с положит. направлением Оу.

Аналогично вводится ось котангенсов.

Геом. интерпрет. позволяет легко установить, что мн-во значении синуса и косинуса ограничено числами 1 и -1, а ось тангенсов и котангенсов не ограничена.

Т. о., изучение эл-ов тригонометрии идет методов УДЕ, т. е. все defs, св-ва, тождества, формулы ПРОБЕЛ

Ключевой явл-ся формула косинус суммы двух углов. Все остальные выводятся из нее.

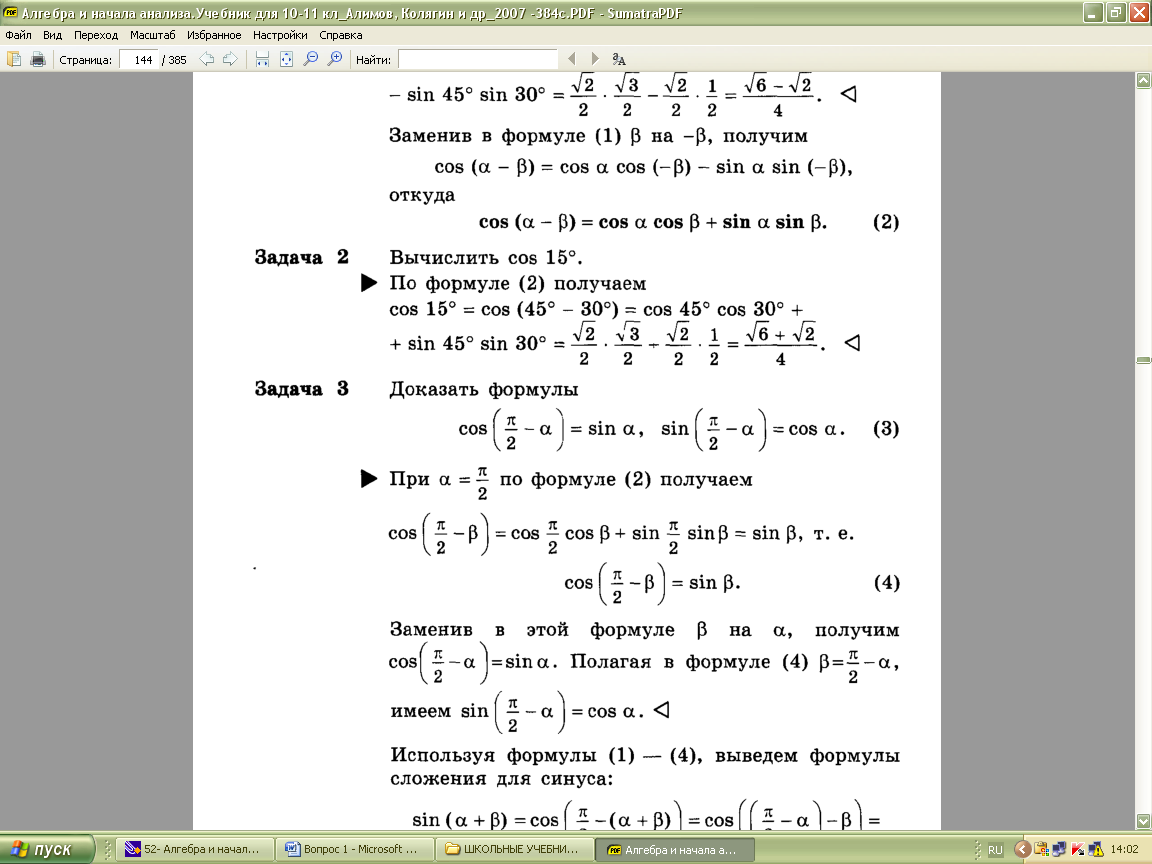
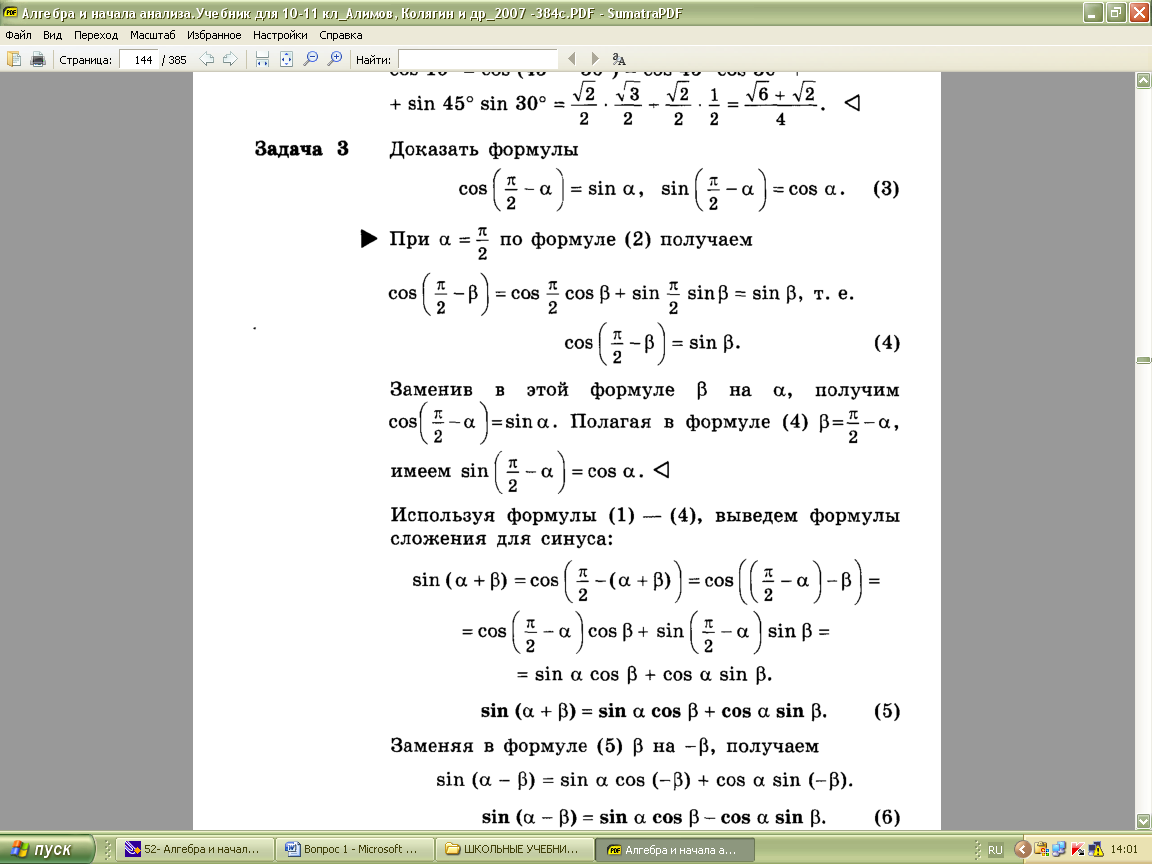
Эту взаимосвязь между формулами учителю нужно четко показать, возможно, на уроке обобщения и систематизации.

Следует обращать внимание на приемы запоминания формул, особенно формул приведения. Отметим, что в учебниках Алимова, в отличии от учебника Мордковича, вначале идет изучение косинуса, синуса, тангенса и котангенса как чисел, рас-ся их св-ва. Т. е. из содержательных линий школьного курса алгебры здесь явно представлена числовая линия.

Далее вводятся формулы тригонометрии, рассм-ся способы док-ва тригоном. тождеств, упрощаются тргоном. выражения, т. е. формируется линия тождественных преобразований, и только потом в тригонометрии рассм-ся линия ур-й и нер-в и функц. линия.