
- •1. Цели и задачи изучения курса алгебры, алгебры и начал анализа в 9-11 классах
- •2. Понятие функции в мат-ке и в школьном курсе мат-ки. Формирование понятия функции в школьном курсе мат-ки
- •3. Знания и умения школьников, связанные с понятием функции. Методика введения понятия функции
- •4. Методика изучения линейной функции
- •5. Методика изучения квадратичной функции
- •6. Методика изучения общих свойств функции
- •7. Расширение понятия степени. Методика введения понятия степени с целым показателем
- •8. Методика введения арифметического корня с натуральным показателем, степени с рациональным показателем
- •9. Определение степени с действительным показателем и её свойства
- •10. Теоретические основы изучения степенной функции
- •11.Урок обобщения и систематизации по теме «Степенная ф-ция»
- •12.Проект изучения темы «Арифметическая и геометрическая прогрессии» (9 класс). Урок решения ключевых задач (метод уде)
- •Глава 4, §§14-16.
- •Глава 4, §§14-16.
- •Ход урока
- •12. Теор. Основы изучения темы «Арифметическая и геометрическая прогрессии»
- •13. Методика изучения показательной функции
- •14. Теоретические основы изучения логарифмической функции. Методика введения понятия логарифма
- •1. Мотивационно-ориентировочный этап
- •2. Содержательный этап.
- •15. Разработка урока-лекции «Логарифмическая функция, её свойства и график»
- •I. Мотивационно-ориентировочная часть.
- •II.Содержательная часть.
- •16. Методические основы введения и изучения элементов тригонометрии: числовая окружность, числовая окружность на координатной плоскости
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •18. Теоретические основы изучения темы «Тождественные преобразования тригонометрических выражений». Урок решения ключевых задач
- •19. Методические рекомендации к изучению тригонометрических функций. Методика изучения свойства периодичности функции
- •21. Проект урока-лекции «Решение уравнений и неравенств Арксинус числа. Свойства арксинуса числа»
- •22. Проект урока-лекции «Решение уравнений и неравенств Арккосинус числа. Свойства арккосинуса числа»
- •23. Проект урока-лекции «Решение уравнений и неравенств Арктангенс числа. Свойства арктангенса числа»
- •24. Методика обучения решению триг. Уравнений и неравенств. Основные приёмы решения триг. Уравнений
- •Семинар-практикум по теме: «Основные приёмы решений тригонометрических уравнений».
- •25. Логические основы решения уравнений и неравенств в старших классах. Методические рекомендации к изучению понятий равносильные уравнения, уравнения – следствия, теорем о равносильности уравнений
- •26. Методика обучения учащихся решению частных видов уравнений и неравенств. Построение урока решения задач (на примере темы «Логарифмические уравнения и неравенства»)
- •2.Операционно-познавательный этап.
- •1. Решите уравнение:
- •2) Решите уравнение: .
- •3) Решите уравнение:
- •4) Решите уравнение: .
- •6) Решить неравенство: .
- •3.Рефлексивно-оценочный этап.
- •27. Организация заключительного повторения в 11 классе темы «Уравнения и неравентсва». Урок-лекция «общие методы решения уравнений»
- •1 Группа.
- •2 Группа.
- •3 Группа.
- •28. Методика введения понятий предела функций в точке и непрерывности функции
- •29. Методика введения понятия производной функции
- •30. Методика изучения геометрического смысла производной, уравнения касательной к графику функции
- •31. Теоретические и методические основы изучения темы «Применение производной к исследованию функции»
- •32. Теоретические и методические основы изучения первообразной и интеграла
- •33. Причины включения в школьный курс математики элементов вероятностно-статистической линии. Основные цели изучения элементов теории вероятностей и математической статистики
- •34. Теоретические и методические основы изучения теории вероятностей в школьном курсе математики 9-11 классов
14. Теоретические основы изучения логарифмической функции. Методика введения понятия логарифма
Ядром изучаемой темы является понятие логарифма и логарифмической функции, которая относится к числу элементарных.
Сначала даётся определение логарифма, основное логарифмическое тождество, рассматриваются свойства логарифма. Выделяются два основных вида логарифмов – десятичные и натуральные, формула перехода от логарифма по одному основанию к логарифму по другому основанию. Устанавливается тот факт, что достаточно только десятичных и натуральных логарифмов, чтобы находить логарифмы чисел по любому основанию.
В данной теме рассматривается новое действие над числами - логарифмирование. Оно является обратным к действию возведения в степень.
Исследование логарифмической функции проводится в соответствии с ранее введённой схемой. Проводится обзор свойств этой функции в зависимости от значения параметров. На примерах показательной и логарифмической функций вводится понятие обратной функции. Раскрывается роль логарифмической функции, как функции обратной к показательной.
Учащиеся уже знакомы со степенной и показательной функции, таким образом, они уже имеют представление о функции как таковой. Степенная и показательная функции основывались на понятии степени с рациональным и действительным показателем. Поэтому изученное ранее понятие логарифма дало основу для введения понятия логарифмической функции. Приступая к введению понятия логарифмической функции необходимо вспомнить определение логарифма и основные логарифмические тождества. При открытии свойств логарифмической функции необходимо провести аналогию с открытием свойств показательной функции.
Серьёзное внимание следует уделить работе с основными логарифмическими тождествами. Рассматриваются логарифмические уравнение и неравенства, для решения которых необходимо усвоить понятие логарифма и его свойства, а также понятие логарифмической функции и её свойства. При решении логарифмических уравнений появляется настоятельная необходимость введения понятий следствия и равносильности. Именно здесь эти понятия и вводятся.
Основная цель - познакомить учащихся с логарифмической функцией и ее свойствами, научить решать несложные логарифмические уравнения и
неравенства, их системы.
При решении логарифмических уравнений используются следующие общие методы решения уравнений:
- метод введения новой переменной,
- функционально-графический метод,
- разложение на множители. Отметим, что решение любого логарифмического уравнения сводится к решению простейшего уравнения одного из двух видов:
1).
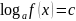 ,
2).
,
2).
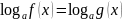
Кроме общих методов можно выделить и специальные методы решения логарифмических уравнений:
Логарифмирование. Это преобразование заключается в переходе от уравнения f(x)=g(x) к уравнению , если f(x)>0.
-
Применение основного логарифмического
тождества.
Данное преобразование основано на
переходе от уравнений
 к уравнению-следствию f(x)=h(x).
к уравнению-следствию f(x)=h(x).
-
Переход к новому основанию логарифма,
используя формулу:
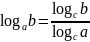 ,
a>0,
a≠1,
b>0,
c>0,
c≠1.
Здесь
возможна потеря корней.
,
a>0,
a≠1,
b>0,
c>0,
c≠1.
Здесь
возможна потеря корней.
- Применение свойств логарифмов.
При решении логарифмических неравенств применяются те же методы, что и при решении логарифмических уравнений. Поэтому логарифмические уравнения и неравенства целесообразно изучать методом укрупнения дидактических единиц. Среди логарифмических неравенств особое место занимают неравенства, содержащие переменную в основании логарифма, поскольку решение таких неравенств вызывает определенные трудности у школьников. Наиболее распространенный способ решения этих неравенств заключается в рассмотрении двух случаев: 1) основание больше единицы; 2) основание положительно и меньше единицы.
В конце изучения данной темы на уроке систематизации и общения целесообразно составить систематизирующую таблицу, в которой отражалась бы вся логическая цепочка, по которой происходило изучение данной темы.
Задачный материал данной темы можно разделить на три основных блока.
1. Задачи на нахождение значения лог. выражений и тождественные преобразования.
Ключевыми задачами этого блока являются:
-
вычислить:
-
вычислить: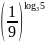
-
вычислить:
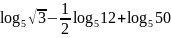
2. Задачи на исследование логарифмической функции и построение ее графика.
Ключевыми задачами этого блока являются, например:
-
Сравнить числа
 и
и
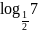
-
Изобразить схематически график функции
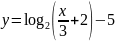
-
Исследовать на монотонность функцию
3. Задачи на решение уравнений (неравенств) и их систем.
Как правило, решение логарифмического уравнения сводится к решению простейшего уравнения одного из следующих видов:
-
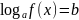
-
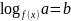
-
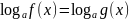
Ключевыми задачами к этим трем видам логарифмических уравнений будут, например, следующие задания:
1).
Решите уравнение
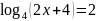
2).
Решите уравнение
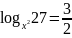
3).
Решите уравнение

Учебная задача:
- раскрыть операцию логарифмирование как операцию обратную потенцированию;
- формировать у учащихся представление о логарифмической функции, как модели процессов реальной действительности;
- выявить в совместной деятельности с учащимися основные способы решения логарифмических уравнений и неравенств различных типов.
Диагностируемые ели: В результате урока ученик:
Знает: опр. логарифма, свойства логарифмов, действие логарифмирования, опр. десятичного и натурального логарифма, свойства логарифмов, основу доказательства свойств; определение лог. функции, формулировку свойств логарифмической функции, формулировку теоремы о монотонности лог. функции, как выглядит и строится график лог. функции; типы лог. уравнений и неравенств, методы и способы их решения.
Понимает: связь между действием логарифмирования и потенцирования; аналогию свойств логарифмической функции со свойствами показательной функции; роль теорем о равносильности уравнений (неравенств), какие преобразования могут привести к потере корней, а какие к приобретению посторонних корней;
Умеет: выполнять преобразования выражений, содержащих логарифмы, на основе определения и свойств логарифма, основного логарифмического тождества; определять значение функции по значению аргумента при различных способах задания функции, строить графики логарифмических функций, выполнять преобразования графиков, описывать по графику и по формуле поведение и свойства функций; решать логарифмические уравнения и неравенства, используя как специальные методы: логарифмирование, применение основного логарифмического тождества и свойств логарифма, переход к новому основанию логарифма, так и общие методы решения уравнений и неравенств: метод введения неизвестного, функционально-графический метод, метод разложения на множители.
Тема урока «Понятие логарифма. Свойство суммы логарифмов»
Тип урока: урок изучения нового
Средства обучения: мел, доска, учебник
Учебные задачи урока: ввести действие лог-ния как обратное потенцированию.
Диагностируемые цели:
В результате изучения темы ученик:
- знает: опр. логарифма числа, основное лог. тождество, опр. действия лог-ния, свойство суммы логарифмов
- умеет: вычислять логарифм числа по опр., формулировать и доказывать свойство суммы логарифмов, применять полученные теоретические знания при решении соответствующих практических задач.
- понимает: связь между действием возведения в степень и лог-нием; что опр. и свойство суммы логарифмов можно применять в обе стороны при некоторых определенных условиях.
Методы урока: проблемное изложение, частично-поисковый.
Формы работы: фронтальная
Структура урока: 1 – 10 минут; 2. -30 минут; 3. – 5 минут
