13. Методика изучения показательной функции

a>0			0<a<1
x<0	x=0	x>0	x<0	x=0	x>0
0< <1	y=1	>1	>1	y=1	<1

C 9 класса общий подход к изучению конкретного вида функций следующий:

1. Рассматривают примеры реальной действительности.

2. Их анализ.

3. Получение математической модели конкретного вида функции.

4. Исследование математической модели аналитическими методами.

5. Переход к графической модели функции

Мотивация к параметрической формуле:

Задача 1. Давление воздуха убывает с высотой подъема по закону , где 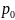-давление на уровне моря h = 0, p-давление на высоте h, H = const (зависит от температуры воздуха).

1. Задача 2. При радиоактивном распаде количество вещества уменьшилось вдвое за сутки. Сколько вещества останется от 250г через 1,5 суток? Через 3,5 суток?

2. Решение:

3. , где T = 1, t₁ = 1,5, t₂ = 3,5, m₀ = 250.

4. Задача 3. На некотором лесном участке можно заготовить 4∙10⁵ м³ древесины. Ежегодный прирост деревьев равен 4%. Сколько можно заготовить древесины на этом участке через 5 лет?.

5. Решение:

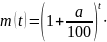6. 4∙10⁵ , где t = 5, a = 4.

- По закону 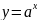изменяются многие процессы реальной действительности, размножение бактерий, восстановление гемоглобина в крови, остывание чайника и т.д. Таким образом, следует изучить функцию вида . Какие ограничения на a?

1. a>0 так как степень с любым действительным показателем существует только при таком условии.

2. a так как в противном случае имеем функцию = 1 это прямая и исследовать нечего.

Формулируется определение показательной функции.

Опр. показательной функцией называется функция вида y = a^x, где а – заданное число, х – переменная, a > 0, a ≠ 1.

Переходим к исследованию свойств на аналитически заданной функции:

1. D(x): R – по определению степени с действительным показателем.

2. E(x): y>0 – по определению степени, чётко доказать в шк. Курсе нельзя.

Док-во: Нужно показать, что уравнение а^х = b, где a >0, a ≠ 1, не имеет корней, если , и имеет корень при любом b > 0. По свойству степени: a^x > 0 это уравнение не имеет корней, если . То, что уравнение имеет корень при любом b>0 означает, что любая прямая у = b пересекается с графиком показательной функции.

3. Нули функции: нулей нет т.к. функция строго положительная

4. Монотонность

a>1 x1 < x2, x > 0, то => y1 > y2 возрастает

0<a<1 x1 <x2, то => y1 < y2 убывает

Доказывается на основе свойств степени. Формируется обратное утверждение: => x₁>x₂ если a>; => x₁< x₂ если 0<a<1. К этому приходят методом от противного.

5. Промежутки знакопостоянства.

Строим 2 графика при a>0 и 0<a<1 используя данные таблицы.

6. Четность / нечетность. Эта функция общего вида

7. Ограниченность. Функция ограниченна снизу, то есть существует горизонтальная асимптота y = 0.

8. Дается схематическое изображение графика функции.

Далее решаются упражнения на узнавание, чтение графика, построение, на использование свойств:

- построить график функции;

- сравнить числа, используя свойство возрастания/убывания функции;

- решить уравнение;

- решить неравенство;

- найти н/б и н/м значение функции.