
- •1. Цели и задачи изучения курса алгебры, алгебры и начал анализа в 9-11 классах
- •2. Понятие функции в мат-ке и в школьном курсе мат-ки. Формирование понятия функции в школьном курсе мат-ки
- •3. Знания и умения школьников, связанные с понятием функции. Методика введения понятия функции
- •4. Методика изучения линейной функции
- •5. Методика изучения квадратичной функции
- •6. Методика изучения общих свойств функции
- •7. Расширение понятия степени. Методика введения понятия степени с целым показателем
- •8. Методика введения арифметического корня с натуральным показателем, степени с рациональным показателем
- •9. Определение степени с действительным показателем и её свойства
- •10. Теоретические основы изучения степенной функции
- •11.Урок обобщения и систематизации по теме «Степенная ф-ция»
- •12.Проект изучения темы «Арифметическая и геометрическая прогрессии» (9 класс). Урок решения ключевых задач (метод уде)
- •Глава 4, §§14-16.
- •Глава 4, §§14-16.
- •Ход урока
- •12. Теор. Основы изучения темы «Арифметическая и геометрическая прогрессии»
- •13. Методика изучения показательной функции
- •14. Теоретические основы изучения логарифмической функции. Методика введения понятия логарифма
- •1. Мотивационно-ориентировочный этап
- •2. Содержательный этап.
- •15. Разработка урока-лекции «Логарифмическая функция, её свойства и график»
- •I. Мотивационно-ориентировочная часть.
- •II.Содержательная часть.
- •16. Методические основы введения и изучения элементов тригонометрии: числовая окружность, числовая окружность на координатной плоскости
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •17. Методические основы введения и изучения элементов тригонометрии: определение синуса, косинуса, тангенса и котангенса числа (угла)
- •18. Теоретические основы изучения темы «Тождественные преобразования тригонометрических выражений». Урок решения ключевых задач
- •19. Методические рекомендации к изучению тригонометрических функций. Методика изучения свойства периодичности функции
- •21. Проект урока-лекции «Решение уравнений и неравенств Арксинус числа. Свойства арксинуса числа»
- •22. Проект урока-лекции «Решение уравнений и неравенств Арккосинус числа. Свойства арккосинуса числа»
- •23. Проект урока-лекции «Решение уравнений и неравенств Арктангенс числа. Свойства арктангенса числа»
- •24. Методика обучения решению триг. Уравнений и неравенств. Основные приёмы решения триг. Уравнений
- •Семинар-практикум по теме: «Основные приёмы решений тригонометрических уравнений».
- •25. Логические основы решения уравнений и неравенств в старших классах. Методические рекомендации к изучению понятий равносильные уравнения, уравнения – следствия, теорем о равносильности уравнений
- •26. Методика обучения учащихся решению частных видов уравнений и неравенств. Построение урока решения задач (на примере темы «Логарифмические уравнения и неравенства»)
- •2.Операционно-познавательный этап.
- •1. Решите уравнение:
- •2) Решите уравнение: .
- •3) Решите уравнение:
- •4) Решите уравнение: .
- •6) Решить неравенство: .
- •3.Рефлексивно-оценочный этап.
- •27. Организация заключительного повторения в 11 классе темы «Уравнения и неравентсва». Урок-лекция «общие методы решения уравнений»
- •1 Группа.
- •2 Группа.
- •3 Группа.
- •28. Методика введения понятий предела функций в точке и непрерывности функции
- •29. Методика введения понятия производной функции
- •30. Методика изучения геометрического смысла производной, уравнения касательной к графику функции
- •31. Теоретические и методические основы изучения темы «Применение производной к исследованию функции»
- •32. Теоретические и методические основы изучения первообразной и интеграла
- •33. Причины включения в школьный курс математики элементов вероятностно-статистической линии. Основные цели изучения элементов теории вероятностей и математической статистики
- •34. Теоретические и методические основы изучения теории вероятностей в школьном курсе математики 9-11 классов
11.Урок обобщения и систематизации по теме «Степенная ф-ция»
Тема урока: «Степенная функция, её свойства и график».Тип урока: урок обобщения и систематизации.Учебная задача: посредством использования различных форм работы на уроке обобщить и систематизировать материал по теме.Диагностируемые цели: в результате урока ученик:
Знает
Определение
функции; Что такое область определения
функции; Определение графика функции;
Что такое множество значений функции;
Определение возрастающей/ убывающей
функции; Определение четной/нечетной
функции; Определение степенной функции;
Общие свойства степенной функции;
Свойства частных видов степенной
функции; Вид графика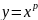 зависит от показателя p;
Определение обратимой функции; Свойства
взаимно обратных функций; График обратной
функции симметричен относительно прямой
зависит от показателя p;
Определение обратимой функции; Свойства
взаимно обратных функций; График обратной
функции симметричен относительно прямой
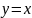 .
.
Умеет: Строить график степенной функции в зависимости от показателя степени; Доказывать свойства степенной функции; Находить обратную функцию к данной; Находить точки пересечения функций; Решать уравнения и неравенства графически; Определять свойства функции (убывание, возрастание); Исследовать функцию на монотонность, на четность и на нечетность; Строить график обратной функции на основе четности, нечётности;
Понимает: От чего зависит вид графика и свойства степенной функции; На основе каких теоретических положений доказываются свойства степенной функции; Какая функция обратимая;
Методы обучения: репродуктивный, метод УДЕ, частично – поисковые. Форма работы: фронтальная, групповая
Средства обучения: мел, доска, учебник, компьютер, проектор, канва – таблица.
Структура урока:1)Мотивационно – ориентировочный этап (10 минут); 2)Содержательный этап (33 минут); 3)Рефлексивно – оценочный этап (2 минут) Для данного урока необходимо предваряющее домашнее задание: Постройте графики функций и выясните их свойства:
-
I вариант

II вариант

III вариант
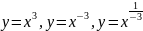
IV вариант

Мотивационно-ориентировочный этап: Актуализация Найти область определения функции (устно, задания в презентации):
Ребята,
скажите, что же называется областью
определения функции? (Областью определения
функции называют множество всех значений,
которое принимает её аргумент)Укажите
промежутки возрастания, убывания
функции. (ученики работают с теми же
рисунками). Ребята, скажите, какая функция
называется возрастающей? (Функция называется
возрастающей на некотором промежутке,
если для любых
называется
возрастающей на некотором промежутке,
если для любых
 и
и
 ,
принадлежащих данному промежутку,
таких, что
,
принадлежащих данному промежутку,
таких, что
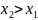 ,
выполняется неравенство
,
выполняется неравенство
 )
Ребята, скажите, какая функция называется
убывающей? Ф-ция
называется
убывающей на некотором промежутке, если
для любых
и
,
принадлежащих данному промежутку,
таких, что
,
выполняется неравенство
)
Ребята, скажите, какая функция называется
убывающей? Ф-ция
называется
убывающей на некотором промежутке, если
для любых
и
,
принадлежащих данному промежутку,
таких, что
,
выполняется неравенство
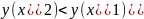 )
Мотивация:
Ребята,
сегодня мы с вами будем повторять и
систематизировать материал, изученный
на прошлых занятиях, который вам
понадобится при выполнении самостоятельной
работы на следующем уроке. Учебная
задача: Подготовиться
к контрольной работе по теме «Степенная
функция». Содержательный
этап Появляется
тема урока: «Степенная
функция, её свойства и график».Ребята,
сегодня в течении урока будем заполнять
канву-таблицу, которая сейчас лежит
перед вами. Вас было задано домашнее
задание, в котором Вы должны были
построить несколько графиков функций
и описать их свойства. Сейчас вы по
вариантам будете выходить к доске,
изображать графики функций и мы вместе
со всеми будем обсуждать свойства этих
графиков. Для начала мы рассмотрим
функции
и
)
Мотивация:
Ребята,
сегодня мы с вами будем повторять и
систематизировать материал, изученный
на прошлых занятиях, который вам
понадобится при выполнении самостоятельной
работы на следующем уроке. Учебная
задача: Подготовиться
к контрольной работе по теме «Степенная
функция». Содержательный
этап Появляется
тема урока: «Степенная
функция, её свойства и график».Ребята,
сегодня в течении урока будем заполнять
канву-таблицу, которая сейчас лежит
перед вами. Вас было задано домашнее
задание, в котором Вы должны были
построить несколько графиков функций
и описать их свойства. Сейчас вы по
вариантам будете выходить к доске,
изображать графики функций и мы вместе
со всеми будем обсуждать свойства этих
графиков. Для начала мы рассмотрим
функции
и
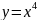 (два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения).
(два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения).
Свойства:
Область определения –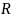 .
Множество
значений –
.
Множество
значений –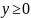 .
Функция
– четная. Функция является убывающей
на промежутке
и возрастающей на промежутке
.
.
Функция
– четная. Функция является убывающей
на промежутке
и возрастающей на промежутке
.
Свойства: Область определения – . Множество значений – . Функция – четная. Функция является убывающей на промежутке и возрастающей на промежутке .
Хорошо, ребята, скажите, к какому классу из представленных принадлежат наши функции и .
I |
|
II |
|
III |
|
IV |
|
V |
|
Давайте
теперь выявим свойства функций,
принадлежащих к классу функций
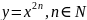 .
.
Свойства: Область определения –множество . Множество значений – . Функция – четная. Функция является убывающей на промежутке и возрастающей на промежутке .
Все результаты заносятся в канву-таблицу.
Далее
мы рассматриваем функции
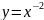 и
и
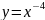 (два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения).
(два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения).
Свойства:
Область определения – множество
,
кроме
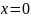 .
Множество
значений
.
Множество
значений
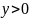 .
Функция
.
Функция
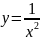 – четная. Функция является убывающей
на промежутке
– четная. Функция является убывающей
на промежутке
 и возрастающей на промежутке
и возрастающей на промежутке
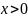 .
.
Свойства:
Область определения – множество
,
кроме
.
.
Множество значений
.
Функция
 – четная. Функция является убывающей
на промежутке
и возрастающей на промежутке
.
– четная. Функция является убывающей
на промежутке
и возрастающей на промежутке
.
Хорошо, ребята, скажите, к какому классу из представленных принадлежат наши функции и
I |
|
II |
|
III |
|
IV |
|
V |
– положительное действительное нецелое число |
(к III классу).
Давайте теперь выявим свойства функций, принадлежащих к классу функций
Свойства
Область
определения – множество
,
кроме
.
Множество
значений – все положительные числа, то
есть
.
Функция
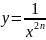 – четная, так как
– четная, так как
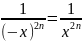 .
Функция является убывающей на промежутке
и возрастающей на промежутке
.
.
Функция является убывающей на промежутке
и возрастающей на промежутке
.
Далее
мы рассматриваем функции
 и
и
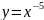 (два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
(два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
Свойства
Область
определения – множество
,
кроме
.
Множество
значений – множество
,
кроме
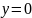 Функция
– нечетная. Функция является убывающей
на промежутке
и
Свойства:
Область определения – множество
,
кроме
.
Множество
значений – множество
,
кроме
.
Функция
– нечетная. Функция является убывающей
на промежутке
и
Хорошо,
ребята, скажите, к какому классу из
представленных принадлежат наши функции
и
.
Функция
– нечетная. Функция является убывающей
на промежутке
и
Свойства:
Область определения – множество
,
кроме
.
Множество
значений – множество
,
кроме
.
Функция
– нечетная. Функция является убывающей
на промежутке
и
Хорошо,
ребята, скажите, к какому классу из
представленных принадлежат наши функции
и
.
I |
|
II |
|
III |
|
IV |
|
V |
– положительное действительное нецелое число |
(к VI классу).
Давайте теперь выявим свойства функций, принадлежащих к классу функций
Свойства
Область
определения – множество
,
кроме
.
Множество
значений – множество
,
кроме
.
Функция
 – нечетная, так как
– нечетная, так как
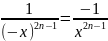 .
Функция является убывающей на промежутке
и
.
.
Функция является убывающей на промежутке
и
.
Далее
мы рассматриваем функции
и
 (два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
(два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
Свойства Область определения – множество . Множество значений – множество . Функция – нечетная. Функция возрастающей на всей действительной оси.
Свойства: Область определения – множество . Множество значений – множество . Функция – нечетная. Функция возрастающей на всей действительной оси. Хорошо, ребята, скажите, к какому классу из представленных принадлежат наши функции и .
I |
|
II |
|
III |
|
IV |
|
V |
– положительное действительное нецелое число |
(к II классу).
Давайте теперь выявим свойства функций, принадлежащих к классу функций
Свойства
Область
определения – множество
.
Множество
значений – множество
.
Функция
– нечетная, так как
 .
Функция возрастающей на всей действительной
оси.
.
Функция возрастающей на всей действительной
оси.
Далее
мы рассматриваем функции
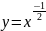 и
и
 (два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
(два ученика выходит к доске, и изображают
графики этих функций, остальные ученики
проверяют их построения)
Свойства Область определения – положительные числа . Множество значений – положительные числа . Функция является убывающей на промежутке .
Свойства: Область определения – положительные числа . Множество значений – положительные числа . Функция является убывающей на промежутке . Хорошо, ребята, скажите, к какому классу из представленных принадлежат наши функции и .
I |
|
II |
|
III |
|
IV |
|
V |
– отрацательное действительное нецелое число |
(к Vклассу).
Давайте теперь выявим свойства функций, принадлежащих к классу функций
Свойства Область определения – положительные числа . Множество значений – положительные числа . Функция является убывающей на промежутке В результате получается заполненная канва – таблица.

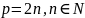
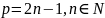
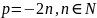
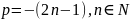
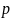 – положительное
действительное нецелое число
– положительное
действительное нецелое число