2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
«Прямая» - неопределяемое понятие в
геометрии.Задана прямая
,
на ней взята т.
- начальная,
,
пусть т.
- текущая. Для
выполняется
условие
- направляющему вектору.Общее свойство
всех точек прямой (условие определяющее
прямую):
.
Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
Пусть дана т.
,
. Через т.
параллельно
можно
провести и единственную прямую (аксиома
параллельных). Следовательно, точкой и
своим направляющим вектором прямая
задается однозначно. Возьмем на плоскости
АСК (косоугольная система координат)
прямую
,
заданную т.
и направляющим вектором
.
Пусть
текущая
точка прямой, было установлено, что
или
(*)
(1 признак коллинеарности) .
а) векторное уравнение прямой:
Покажем
на чертеже
и
(рис.)
,
получаем,
,
где
,
,
.
б) параметрическое уравнение прямой
Условие (*) запишем в координатах.
(1)
В уравнение входит число
,
которое называется параметром,
,
каждому значению
соответствует
единственная точка на прямой, и обратно.
в) каноническое уравнение прямой
Условие (*) по 2 пр. коллинеарности можно
записать так:
(2) более корректно (по 3 пр. коллинеарности)
(3), т.к. среди координат
и
одна может быть равна 0.
(НЕ НАДО: уравнение по 2 точкам:
уравнение по точке и вектору
нормали:
.)
Теорема об общем уравнении прямой:
Пусть задана АСК
и прямая
,
точкой
и направляющим вектором
.
Тогда уравнение прямой записывается в
каноническом виде
,
т.к.
,
то хотя бы одна из его координат не равна
0. В полученном уравнении, ни один из
коэффициентов не равен 0. Следовательно,
уравнение 1-ой степени, а линия, которая
задана уравнением 1 степени называется
линией 1-го порядка, следовательно,
прямая – линия 1-го порядка. Верно и
обратное: всякое уравнение от двух
переменных x и y,
т.е. уравнение вида
(4) определяет на плоскости прямую линию
.
Пусть
,
тогда (3)
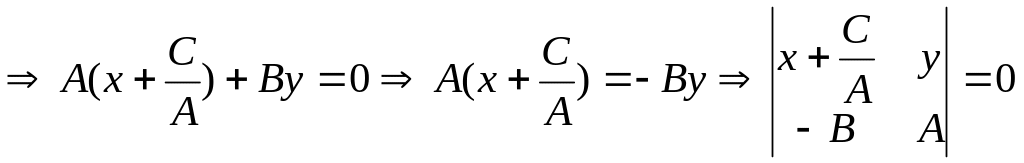уравнение
вида (3).Оно определяет прямую через т.
,
тогда и равносильное ему уравнение (4)
задает ту же самую прямую. Итак, уравнение
(4) – общее уравнение прямой на плоскости.
Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
Пусть на плоскости задана АСК и 2 прямые
своими общими уравнениями:
.
Исследование взаимного расположения
2-х прямых сводится к выяснению, имеют
ли прямые общие точки, сколько их, и
пересекаются ли вообще?
Решение сводится к исследованию систем
уравнений этих прямых:
(1)
После элементарных преобразований (1)
можно привести к виду:
,
где
- определители.
Случай 1:
имеет
единственное решение – координаты
точки общие для 2-х прямых, следовательно,
координаты точки пересечения.
Случай 2:
система несовместна, следовательно, решений не имеет, т.е. прямые параллельны.
Случай 3:
равенство
выполняется при
система
имеет бесчисленное множество точек
и
.
Доказано, что 2 прямые заданные общим уравнением (1): 1. Пересекаются, если коэффициенты при неизвестных пропорциональны. 2. Параллельны, если коэффициенты при неизвестных пропорциональны, но не пропорциональны свободные члены. 3. Совпадают, если коэффициенты при неизвестных и свободные члены пропорциональны.
Угол между двумя прямыми
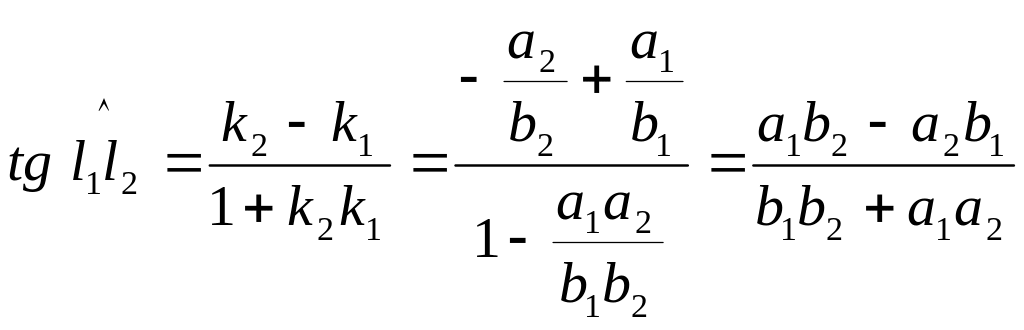
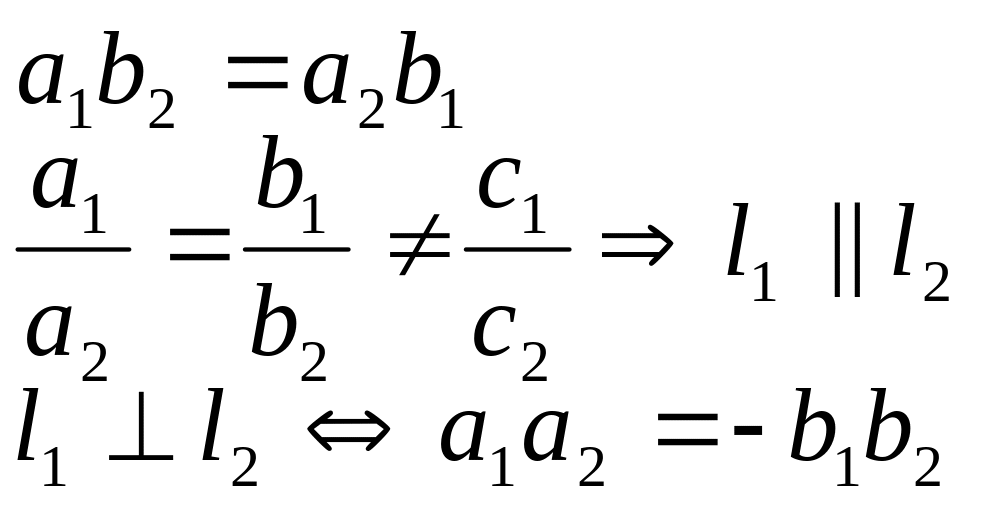
Билет №10