2. Простые и составные числа. Бесконечность мн-ва простых чисел.

Опр. Натуральное число a>1 наз. простым, если оно делится только на ±1 и ± a. В противном случае наз. составным.Нат. число а>1 наз. составным, если сущ. нат. число b≠1, а и b|а.Св-ва простых чисел:

1. Наимен. делитель р среди неединичных делителей числа а>1 яв. простым.

↓ Пусть p- не простое число => 1<p₁<p: р₁|р. Т.к. р|а, что противоречит выбору р.↑

2. Если р-наименьший неединичный делитель составного числа а, то р≤

↓По условию 1. р яв. простым и а=рb. А т.к. а-составное, то b>1. В силу выбора р имеем b≥p∙(p) a=bp≥p²=> p≤ ↑

3. Если р- простое, а-произв. нат., то р|а или р и а-взаимно простые.

↓Т.к. р-простое, то . Если (а,р)=1, то р не | а. Если (а,р)=р, то р|а.↑

4. Если р-простое, р|а∙b, то р|а или р|b.

↓Пусть р не | а. Тогда по 3. => (р,а)=1. В силу условия => (ab,p)=(b,p)=p => p|b.↑

Теорема Евклида: Множество простых чисел бесконечно.

↓ (от противного) Пусть мн-во простых чисел конечно и пусть р₁, р₂, …, р_n – все простые числа.

Составим число а= р_1∙р_2∙ … ∙р_n+1. По предположению оно составное. Пусть р-наименьший неединичный делитель. По св-ву 1 р-простое и р = р_i для некот. i. Тогда

p|а - р₁р₂ … р_n = 1, что невозможно. => множество простых чисел бесконечно. ↑

Теорема (о каноническом разложении): Нат. число > 1 разлагается в произведение простых множителей, причем единств. образом с точностью до порядка множителей.

↓Пусть aєN, а≠1.

1) а – простое => разложение есть.

2) а – составное, то у него есть простой делитель а=p₁∙a₁(p₁-простой делитель.)

Если а₁- простое, то теорема док-на.

Если а₁ – сост., то для него находим простой делитель р₂, а₁= а₂∙р₂ и т.д.

1<а₁<a

а₂<а₁, а>а₁>а₂>а₃…-ряд натур.чисел (убывающий => всегда будет разложение)

Докажем единств-ть:Пусть даны 2 разлож-я: a=p₁…p_n=q₁…q_m по св-ву простых чисел следует p₁(прост.)| q_1…q_m => p₁|q₁(прост.)  когда p₁=q₁.

p₂…p_n=q₂…q_m аналог-но с p_2, q₂ и т.д.

n<m, то след-но 1=q_n+1…q_m ,но это невозможно, т.к.q_n+1 ≠1, а их произвед-е > 1=> n=m.

Если а=p₁…p_n, p_i повторяется k раз.

Говорят, что p_i явл-ся к кратным множителем.

, р_i – различны. ↑

Билет №23

1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.

Опр.1. Комплексному числу z=x+ i на компл. пл-ти соотв. радиус-вектор Оz с коорд. Оz(x,y).

Если z≠0, то радиус-вектор Oz однозначно определяется 2 величинами: 1) длиной вектора |Oz|=r; 2) углом между Ох и вектором Oz в напр. против часовой стрелки.

И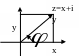 з тригоном. следует (по определению sin и cos): х= cos = r cos , у= sin = r sin , z =x + iy = cos + i sin = ( cos +i sin ) (*)

Представление компл. числа в виде (*) наз. тригонометрической формой комплексного числа.

Заметим, что положение в-ра Oz опр-ся с точностью до углов кратных 2π, т.е.z = r(cos +isin ) = r(cos( +2πk) + isin( +2πk)), k €Z.Углы +2πk наз. аргументами комплексного числа.Угол 0≤ <2π из (*) наз. главными аргументами, обозн. arg z.Пусть z₁=|z₁| ( cos +i sin ), z₂=|z₂| ( cosψ+i sinψ) заданы в триг. форме. Найти z₁ z₂.

z₁ z₂=|z₁| ( cos +i sin )∙|z₂| ( cosψ+i sinψ)= |z₁| |z₂|[(cosψ∙cosφ – sinφ∙sinψ)+i(sinφ∙cosψ+cosφ∙sinψ)]

z₁ z₂= ( cos ( + )+ i sin( + ) ) – ф-ла произведения в триг. форме.

Пусть z= ( cos +i sin ), тогда n Z: zⁿ= ( cos n + sin n )-формула Муавра.

Б.И. n=0, n=1, выполняется в силу условия.

П.И. Формула справедлива для показателей < n (n>1).

Ш. И. Показатель = n. Имеем zⁿ= z^n-1 z=(|z|(cos +isin )^-1)∙(|z|(cos +isin ))=(П.И.)=|z|^n-1(cos (n-1) + isin (n-1) ) ∙( ( cos + isin ))= ( cos n +i sin n ) – справ. Сл-но, по ПМИ ф-ла верна.

Опр. 2. Корнем n-ой степени (n N) из комплексного числа z, z 0, наз-ся комплексное число n-ая степень которого равна данному. Обозн.: .(n = : ).Теорема. 1) Для любого отличного от нуля компл. числа и любого нат. числа n существует точно n корней n-ой степени из данного числа. 2) Мн-во всех корней т-ой степени из компл. числа z= ( cos +i sin ) состоит из след. чисел: ( , k= .

, тогда z= ( cos + i sin ), . Если = (cos + ) яв. корнем n-ой степени из z, то (а). Найдем из условия (а). По ф-ле Муавра:

ⁿ= ⁿ(cos n + ) = ( cos + i sin )

корень n-й степени . из (а) является корнем n-й степени из Z, и т.к.

2-й период sin x и cos x компл. числа вида = ( различны и являются корнями.

Пусть m , m , разделим m с остатком на n, т.е. представим m в виде m=sn+k, 0 (это всегда можно сделать), тогда = ( = ( =

= , k= . Заметим, что произвольному k= соотв. различные корни.

Т.о. ( .

Пример: Решение: Находим триг. форму: z= ( cos +i sin ), =1, , z =( cos +i sin ),

Применяем формулу kорней = 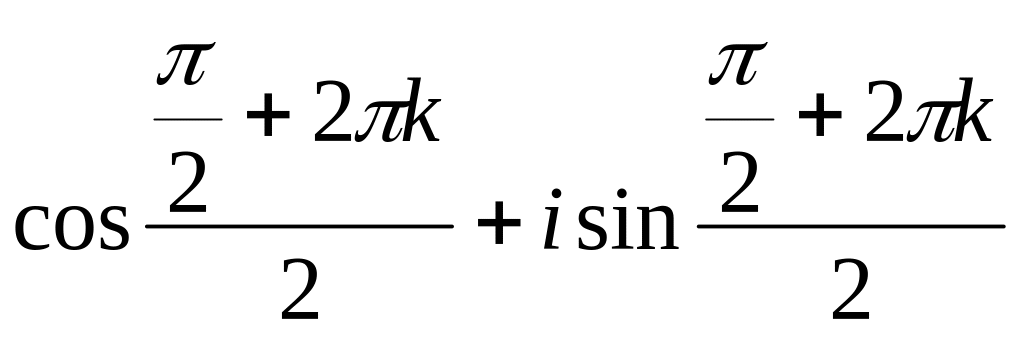, k=0,

cos = , cos

2.Группа афф. Преобраз. плоскости, её основные подгруппы. Опред. аф. геометрии по Ф. Клейну.

Преобразование плоскости называется аффинным, если оно любые три точки и , лежащие на одной прямой, переводит в три точки и , лежащие на одной прямой, и сохраняет их простое отношение, т.е. . Т.к. преобразование подобия прямую переводит в прямую и сохраняет простое отношение трех точек, то любое преобразование подобия является аффинным преобразованием. Поэтому любое движение, в частности тождественное преобразование, является аффинным преобразованием. Свойства аффинных преобразований: 1) По свойствам координат аффинное преобразование является взаимно однозначным отображением плоскости на плоскость: - каждая точка имеет образ и притом только один; - разные точки имеют разные образы; - каждая точка области значений имеет прообраз. 2) Так как аффинное отображение сохраняет координаты точек, то оно сохраняет уравнения фигур. Отсюда следует, что прямая переходит в прямую. 3) Преобразование, обратное к аффинному, есть снова аффинное преобразование. 4) Точки, не лежащие на одной прямой, переходят в точки, не лежащие на одной прямой, а, значит, пересекающиеся прямые - в пересекающиеся прямые, а параллельные – в параллельные. 5) При аффинных преобразованиях сохраняются отношения длин отрезков, лежащих на одной или параллельных прямых. 6) Отношения площадей многоугольников также сохраняются. Лемма. Если аффинные преобразования и переводят две точки и соответственно в точки и , то , где - любая точка прямой . Теорема. Пусть и - произвольные реперы плоскости. Тогда существует одно и только одно аффинное преобразование, которое переводит репер в репер . При этом любая точка с данными координатами в репере переходит в точку с теми же координатами в репере . 1) Докажем сначала, что существует аффинное преобразование, которое переводит репер в репер . Построим преобразование плоскости следующим образом. Произвольной точке с координатами в репере поставим в соответствие точку с теми же координатами в репере . Ясно, что отображение является взаимно однозначным отображением плоскости на себя, т.е. преобразованием, которое репер переводит в репер . Докажем, что - аффинное преобразование. Пусть и - три произвольные точки одной прямой, которые в репере имеют координаты . Их образы в репере имеют те же координаты . Если , то Эти равенства показывают, что точка делит отрезок в отношении , т.е. . Таким образом, точки и лежат на одной прямой и . 2) Докажем теперь, что если - какое-то аффинное преобразование, которое переводит репер в репер , то совпадает с . Пусть - произвольная точка плоскости. Через эту точку проведем прямую так, чтобы она пересекала какие-нибудь две из прямых и в различных точках и . По лемме . Отсюда, используя лемму, получаем: . Таким образом, отображения и совпадают, т.е. - единственное аффинное преобразование, которое переводит репер в репер . При этом аффинном преобразовании точка переходит в точку . Обозначим через - множество всех аффинных преобразований плоскости. Докажем, что если , то . Действительно, т.к. и - преобразования, то - преобразование. Но каждое из преобразований и переводит три точки, лежащие на одной прямой, в три точки, лежащие на одной прямой, и сохраняет их простое отношение, поэтому преобразование обладает теми же свойствами, т.е. является аффинным преобразованием. Таким образом, . Далее, если , то . Действительно, если точки и лежат на одной прямой, то их образы также лежат на одной прямой, ибо если предположить обратное, то найдется такой репер , который в преобразовании переходит в три точки , лежащие на одной прямой, что невозможно. При этом, очевидно, преобразование сохраняет простое отношение трех точек. Таким образом, множество всех аффинных преобразований образует группу. Она называется группой аффинных преобразований плоскости. Основным инвариантом этой группы является простое отношение трех точек. Группа подобий плоскости является подгруппой группы ; группа всех движений также является подгруппой группы Другими примерами подгрупп являются: а) множество всех аффинных преобразований первого рода; б) множество всех аффинных преобразований, для которых - неподвижная точка; в) множество всех аффинных преобразований, для которых прямая состоит из неподвижных точек. Аффинная геометрия изучает свойства фигур, которые сохраняются при любых аффинных преобразованиях, то есть инвариантные относительно таких преобразований. Понятие «аффинная геометрия» возникло в связи с Эрлангенской программой Ф. Клейна (1872 г.), согласно которой каждой группе преобразований отвечает своя геометрия, изучающая свойства фигур, инвариантные относительно преобразований этой группы

Билет №24