1. Основные теоремы дифференциального исчисления.
Теорема Ферма. Пусть функция
f(x)
определена и непрерывна на промежутке
X и во внутренней точке
имеет
наибольшее и наименьшее значения. Если
в этой точке
производ.
функ., то
=0.
↓Докажем случай когда - наибольшее значение функции на всём промежутке.
=
,
т.к. в
-
наибол. значение, то
.
1). Если x<
,
то x-
<0,
,
=
(одно
из св-в пределов).
2). Если x>
,
то x-
>0,
,
(из подчёркнутого)
=0
↑
Геометрический смысл теоремы:
kкас=
=0
касательная
// Ох.
Теорема Ролля. Пусть функция f(x) удовлетворяет следующему условию:
1) Она определена и непрерывна на отрезке [a;b];
2) дифференцируема на интервале (a;b);
3) f(a)=f(b),
тогда
,
такая что
.
Геометрический смысл теоремы: Начертим график непрерывной дифференцируемой функции.
такая,
что kкас=
,
касательная // Ох.
Теорема Лагранжа. Пусть функция
f(x)
непрерывна на отрезке [a;b]
и дифференцируема на интервале (a;b),
тогда
,
такая что
=
,
т.е.
.
Г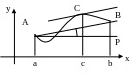
еометрический
смысл теоремы: kсек=
=
,
тогда
,
такое что
касательная //секущей, т.е. kкас.=kсек., т.е. = .
Таких точек может быть и не одна.
Теорема Ролля есть частный случай т.
Лагранжа, когда
2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
Смешанным произв.трех векторов 
,
взятых в указанном порядке, наз.
число, равное скалярному
произв.[
]
.Установим
геометрический смысл смешанного
произведения некомпланарных векторов
.Теор.1
Смешанное произведение 3-х некомпланарных
векторов
,
по модулю равно объему параллелепипеда,
построенного на этих векторах как на
ребрах.
По опр. .[
]
),
- некомплан., отлож.от одной точки.
Достроим до параллепипеда(рис) ОАDBC
,
CH – высота. V=Sосн.CH.
Sосн=
.
Обоз. через 
).
Возможны случаи:1) 0
,
CH=
.
V=
;2)90
.
CH=
V=
.
Следствие.1 Если (
)
– ортонормированный базис, то смешанное
произведение
,
если (
)
– правая,
,
если (
)
– левая.
Геометрическое св-во:
Теор.2
=0
, когда
-
компланарны.
-
компланарны => они линейно зависимы
.
Необходимость:
Дано:
=>
-
компланарны.
Доказать:
-
компланарны.
-
компланарны
.
Следствие.2
-
некомпланарны.
Опр. Тройка векторов называется ориентированной, если указан ее порядок.
Опр. Параллелепипед, построенный на называется ориентированным положительно, если - правая, и отрицательно, если -левая.
Опр. Объем ориентированного параллелепипеда считается положительным, если - правая, и отрицательным, если - левая.
Алгебр.св-ва смеш.произв.: 1) 
;
.2)
(
.
Спаведливость всех свойств вытекает
из свойств определителя.
Смешанное произведение в координатной
форме:
Пусть в (
)
даны
Теор.3
,
Следствие.3
-
компланарны, ,
когда
(*)
– условие компланарности.
Замечание. Условие (*) компланарности
3-х векторов имеет такой же вид, что и в
базисе (
).
Следствие.4
-
некомпланарны 
(**)
Условие (**) называется условием некомпланарности и имеет такой же вид и в афинном базисе.
Применение: Лежат ли 4 точки в одной плоскости? A(1,1,0), B(-1,0,3), C(-2,2,1), D(2,3,0)
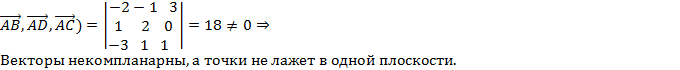
Билет №8