1.Сумма, произведение, частное и композиция непрерывных функций.

Пусть ф-ия определена в т. и в некот.окр-ти этой т. Функция f наз.непрер. в т. ,если

1)

2)Посл-ти:

3)

Опр: Ф-я f(x) назыв. непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка Х.

Теорема 1. Если ф-ии непрерывны в точке х₀, то их сумма, произведение и частное непрерывны в точке х₀.

↓ Пусть ⇒

Теорема 2. Если ф-ия , а непр. в т. , то сложная ф-ия

– непрер.в т.

↓Возьмем Т.к. ф-ия ,то Т.к. ф-ия или

2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.

Пусть — кольцо многочленов от над коммутативным кольцом К с единицей.

Пусть — множество подстановок степени n.

Многочлен от n переменных над коммутативным кольцом наз. симметрическим, если он не изменяется при переименовании (перестановке) переменных.

Пример. f(x₁,…x_n) = симметрический.

f(x₁,…x_n) = х₁²х₂²х₃ + х₁⁵х₂х₃⁴ – не симметрический.

Элементарными симметрическими многочленами от n-переменных называются многочлены:

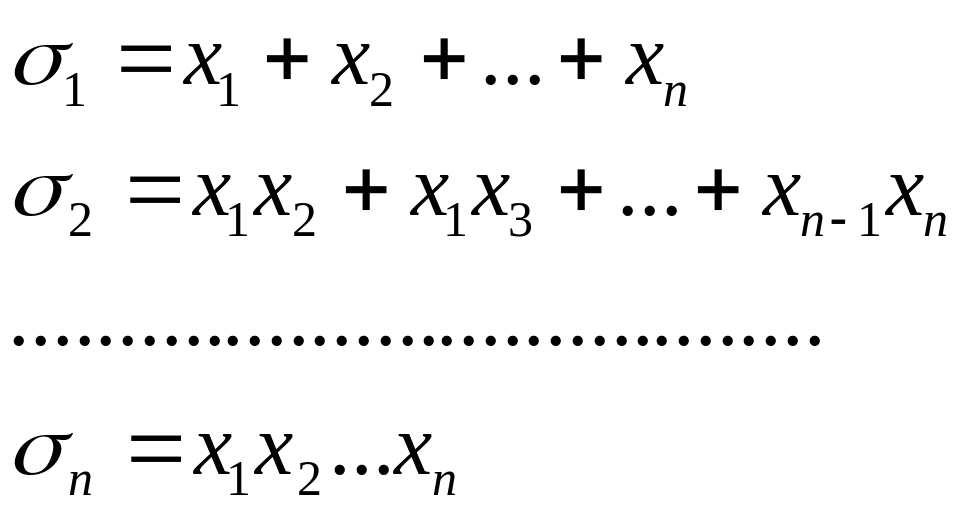
Мн-во всех симметр. мн-нов из образ. подкольцо в кольце мн-нов .

Непустое подмн-во А кольца К наз. подкольцом, если вып. усл.: a,bA => a-bA; 2) a,bA => a∙bA.

Леммы о симметрических многочленах.

Пусть — кольцо многочленов от .

Лемма1 (о старшем члене симметрического полинома). Если -старший член симметрического многочлена f(x₁,…x_n), то .

Лемма 2 (о представлении старшего члена симметрического полинома). Если - старший член ненулевого симметрического многочлена f , то он совпадает со ст. членом произведения .

Лемма 3(об отн. порядка < на симметр. полиномах). Убывающая цепь для симметр. мн-нов обрывается.

Осн. теор. о симметр. мн-нах. Всякий симметрический многочлен из кольца многочленов можно алгебраически выразить через элементарные симметрические многочлены , т. е.

; .

↓ Пусть f — ненулевой симметриче­ский многочлен над К и — его старший член.

Мн-н (1) — симметр., как разность симметр. мн-нов, причем, по лемме 2, f>f₁. Пусть высший член мн-на f₁. Ан-но, мн-н (2) f₂= яв-ся симметр., причем f₁>f₂ и т. д. В р-те получ. убывающая цепочка симметр. мн-нов f₀> f₁ >f₂>f₃>…>f_n>… По лемме 3, эта цепочка не может быть бесконечной. Предположим, что она обрывается на (s+l)^m шаге, т. е.

Складывая почленно рав-ва (1), (2),..., (s +1), получ.

Это равенство дает искомое представление симметрического многочлена f в виде многочлена над К от элементарных сим­метрических многочленов .

Единственность: предположим, что ↑

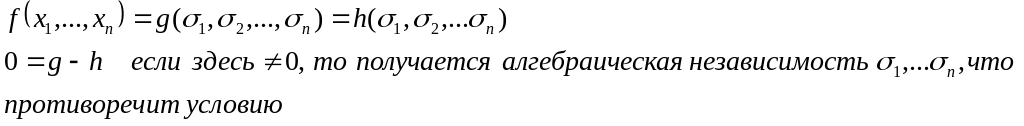Пример:

Следствие. Пусть , Р- поле.

Всякое поле Р можно расширить до такого поля , в котором мн-н n-степени имеет n-корней.

f имеет корни с_1,с₂,…с_n получим формулы Виета

(1) с₁+ с₂+…+ с_n= -

……………………………………..

(2) с₁ с₂+ с₁ с₃+…+с_n-1c_n=

…………………………………….

(3) с₁с₂…с_n=(-1)ⁿ

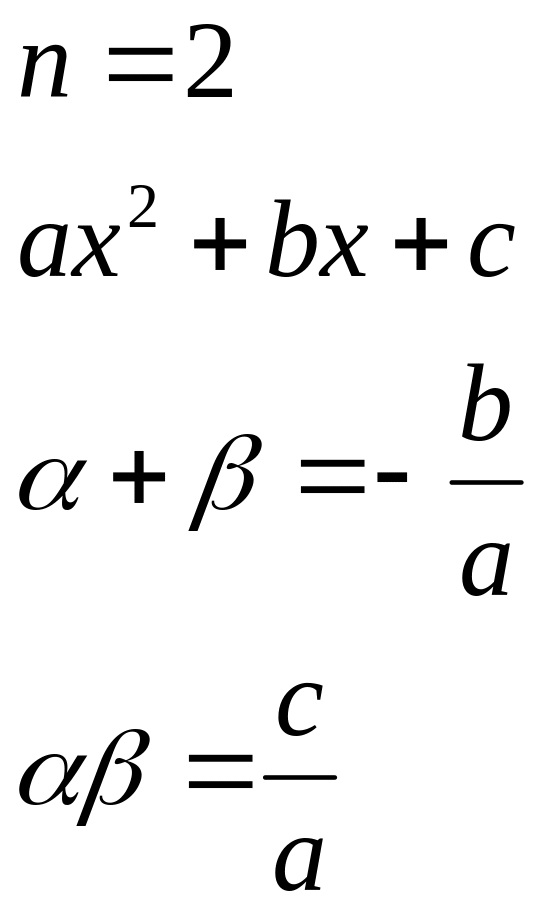
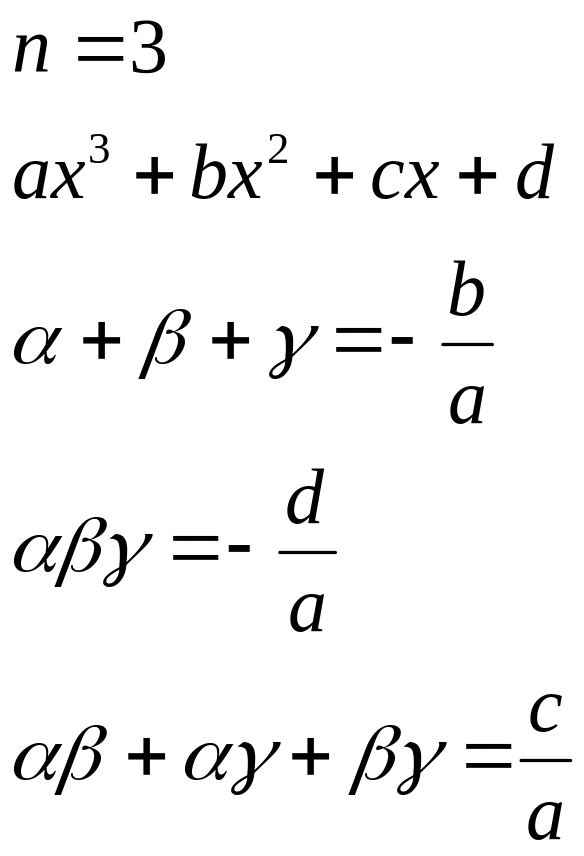(эти случаи только знать) ↑

↓

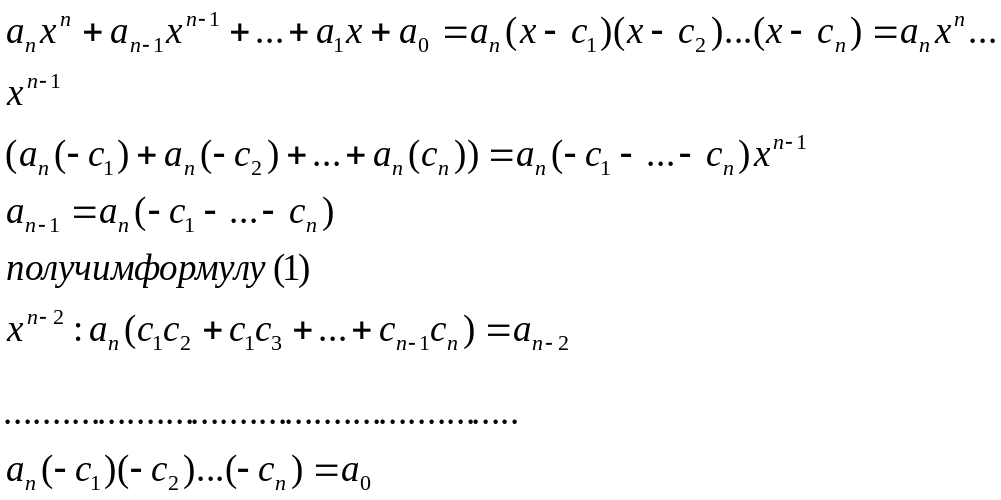Билет №5.