
- •1. Теорема Вейерштрасса о пределе монотонной последовательности.
- •2. Понятие вектора. Линейные операции над векторами и их св-ва.
- •1. Эквивалентность определений предела функции по Коши и Гейне.
- •1. Основные свойства предела функции.
- •1.Сумма, произведение, частное и композиция непрерывных функций.
- •2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.
- •1. Свойства функций непрерывных на отрезке.
- •2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач
- •Геометрические свойства
- •Алгебраические свойства
- •1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.
- •2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.
- •1. Основные теоремы дифференциального исчисления.
- •2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
- •1. Необходимые и достаточные условия возрастания и убывания функции.
- •2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
- •1. Необходимые и достаточные условия локального экстремума функции.
- •2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
- •Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
- •Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
- •1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.
- •Линейные свойства интеграла Римана.
- •Свойства, связанные с неравенствами.
- •1. Достаточное условие существования определенного интеграла.
- •2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
- •1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.
- •2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.
- •2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
- •7.3. Взаимное расположение двух плоскостей.
- •2. Отношение сравнения целых чисел, свойства. Сравнения первой степени.
- •1. Необходимые и достаточные условия дифференцируемости ф-ций комплексной переменной. Понятие аналитической ф-ции в точке и в области.
- •Счетность множества рациональных чисел.
- •1. Несчетность множества точек отрезка [ 0,1 ]
- •2. Кольцо классов вычетов, приведённая система классов вычетов.
- •1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.
- •2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.
- •1. Векторные пространства, простейшие свойства, примеры векторных пространств. Подпространства.
- •Применение гомотетии (подобия) к решению задач на построение (или на доказательство).
- •Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.
- •2. Простые и составные числа. Бесконечность мн-ва простых чисел.
- •1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.
- •1.Классификация движений второго рода плоскости, их применение к решению геом. Задач.
- •2. Системы линейных ур-ий, их виды. Равносильные системы линейных ур-ий. Метод исключения неизвестных, критерий совместности и неразрешимости.
- •2. Изображение пространственных фигур в параллельной проекции.
- •2.Взаимное расположение двух прямых на плоскости Лобачевского.
- •2. Изображение плоских фигур в параллельной проекции.
- •14 Вопрос. Проективная плоскость (пп) и ее модели.
- •19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
1. Необходимые и достаточные условия возрастания и убывания функции.
Опр. 1: Функция f(x)
называется возрастающей в широком
смысле на множестве Х, если
![]()
![]()
![]() .В
частности, если всегда
.В
частности, если всегда
![]() функция наз. возрастающей в узком
или строгом смысле.Опр. 2:
Функция f(x)
называется убывающей на Х в широком
смысле, если
функция наз. возрастающей в узком
или строгом смысле.Опр. 2:
Функция f(x)
называется убывающей на Х в широком
смысле, если
![]() .В
частности, если всегда
.В
частности, если всегда
![]() функция наз. убывающей в узком или
строгом смысле. Опр. 3:
Возрастающие и убывающие функции наз.
монотонными (в узком или строгом
смысле).Теорема 1: Пусть
функция f(x)
определена и непрерывна на [a, b] и
дифференцируема на (a, b), тогда f(x)
возрастает (убывает) в широком смысле
на отрезке тогда и только тогда, когда
функция наз. убывающей в узком или
строгом смысле. Опр. 3:
Возрастающие и убывающие функции наз.
монотонными (в узком или строгом
смысле).Теорема 1: Пусть
функция f(x)
определена и непрерывна на [a, b] и
дифференцируема на (a, b), тогда f(x)
возрастает (убывает) в широком смысле
на отрезке тогда и только тогда, когда
![]() на
(a, b).
на
(a, b).
1) Необходимость. Если f(x)
возрастает на [a, b], то
![]() на (a, b).
на (a, b).
Возьмем любую
![]() ,
любое
,
любое
![]() причем такие, что
причем такие, что
![]() ,
то в силу возрастания функции следует
,
то в силу возрастания функции следует![]() ,
тогда дробь
,
тогда дробь
![]() ,
следовательно
,
следовательно
![]() .
.
2) Достаточность. Если на (a, b), то f(x)- возрастает на [a, b].
Возьмем любое
![]() и
и
![]() такие, что
такие, что
![]() .
Составим разность
.
Составим разность
![]() .
Применим теорему Лагранжа:
.
Применим теорему Лагранжа:
![]() ,
получается, что
,
получается, что
![]() .■
.■
Теорема 2: Пусть функция
f(x) определена
и непрерывна на [a, b] и дифференцируема
на (a, b). Если
![]() (
(![]() )
на (a, b), то f(x)
возрастает (убывает) на [a, b].
)
на (a, b), то f(x)
возрастает (убывает) на [a, b].
Рассмотрим случай
.
По теореме Лагранжа
![]()
![]() ,
то
,
то
![]() ,
,
![]() .■
.■
З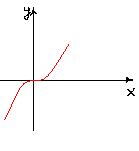 амечание:
Эта теорема является достаточным
признаком возрастания и убывания
функции. Обратное предложение не верно.
амечание:
Эта теорема является достаточным
признаком возрастания и убывания
функции. Обратное предложение не верно.
Пример: (на неверно) y=x3
возрастает на R
![]() x=0,
x=0,
![]() касательные совпадают с осью ОХ.
касательные совпадают с осью ОХ.
2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
Пусть
![]() ,
т. е.
,
т. е.
![]()
Предложение: Если
![]() яв. корнем f(x)
яв. корнем f(x)![]() ,
то
,
то
![]() также
яв-ся корнем f(x).
также
яв-ся корнем f(x).
↓ Испол. св-во сопряжения:
![]() ;
;
![]() ;
;
![]() =>
=>
![]() .
↑
.
↑
Многочлен полож. ст. над R наз. неприводимым, если его нельзя представить в виде произведения двух многочленов меньшей степени.
Теорема: Неприводимый многочлен над R имеет степень ≤ 2.
↓Пусть
![]() ,
по основной теореме алгебры существует
корень
,
по основной теореме алгебры существует
корень
![]()
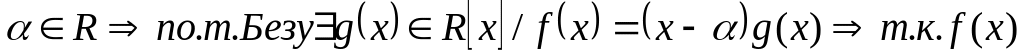 неприводим
неприводим
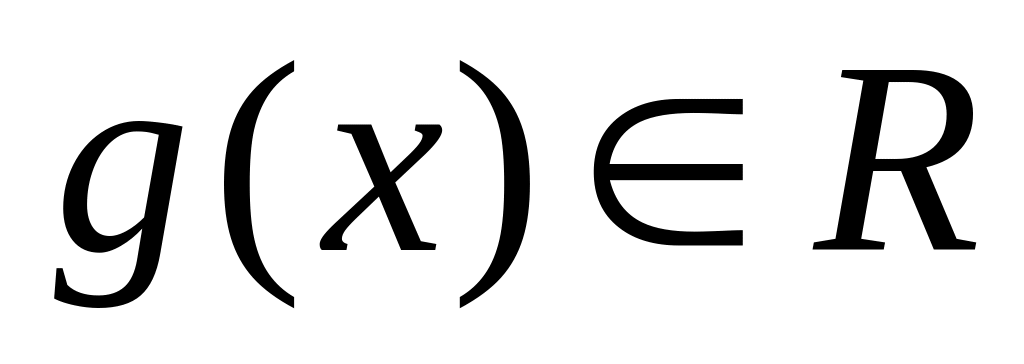 ,
т. е.
,
т. е.
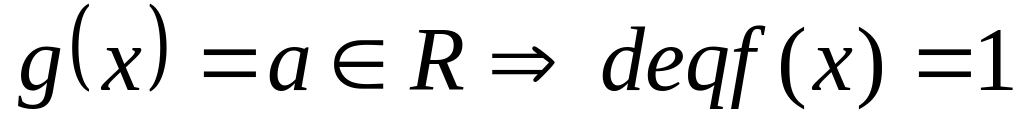 .
.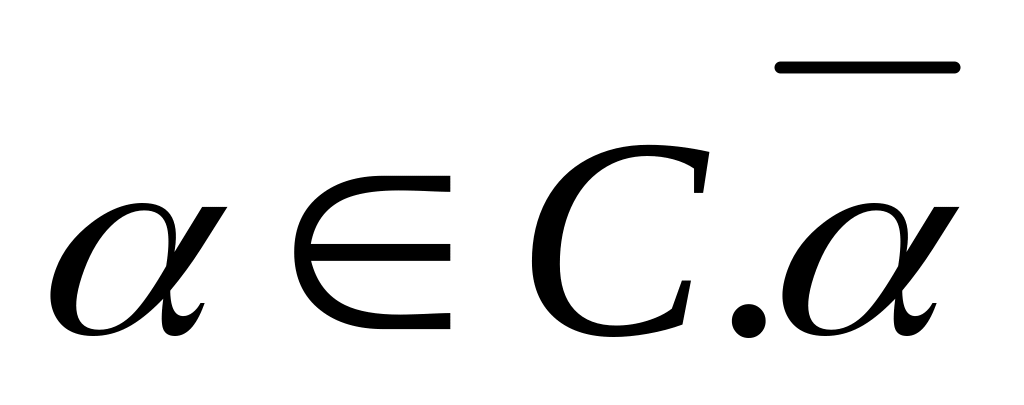 также корень (по лемме). По предложению
также корень (по лемме). По предложению
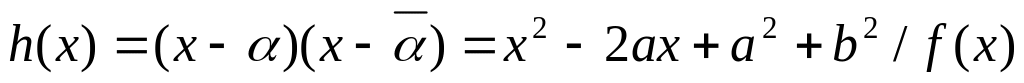 и
и

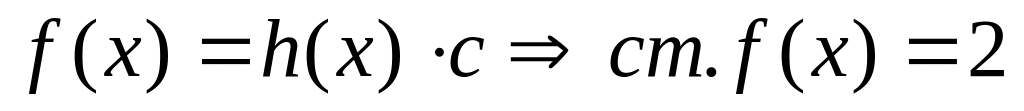 ↑
↑
Следствие: Если
,
то его можно представить в виде
![]() ,
где
,
где
![]() не превышает квадрата трехчлена, т. е.
не превышает квадрата трехчлена, т. е.
![]() .
.
Теорема Безу: Пусть
![]() многочлен
над коммутативным кольцом с единицей
К и пусть
многочлен
над коммутативным кольцом с единицей
К и пусть
![]() ,
тогда
,
тогда
![]() ,
где f(c)
наз. остатком.
,
где f(c)
наз. остатком.
Основная теорема алгебры: Многочлен положител. степени над полем С имеет хотя бы один корень.
(Дополнительно) Свойства сопряжения:
. 2)
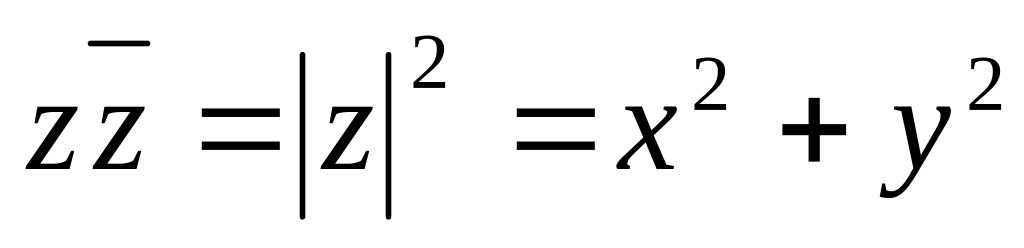 3)
4)
3)
4)
5)
![]() 6)
6)
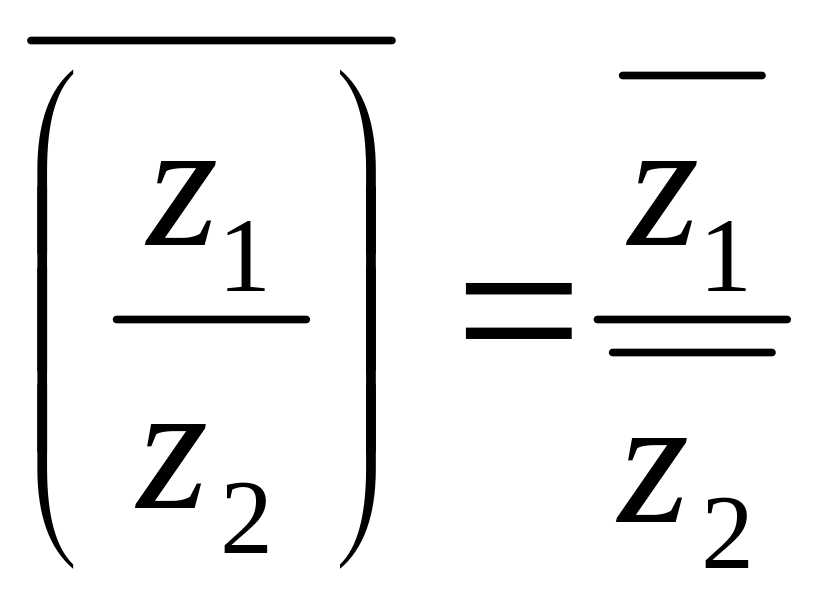 7)
7)
![]()
Билет №9
1. Необходимые и достаточные условия локального экстремума функции.
О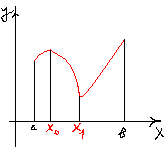 пр.
1: Точка х0 называется
точкой максимума f(x),
если у точки х0 имеется такая
окрестность, что при любом х из этой
окрестности выполняется неравенство
пр.
1: Точка х0 называется
точкой максимума f(x),
если у точки х0 имеется такая
окрестность, что при любом х из этой
окрестности выполняется неравенство
![]() .
.
Опр. 2: Точка х0 называется
точкой минимума f(x),
если у точки х0 имеется такая
окрестность, что при всех значениях х
этой окрестности выполняется неравенство
![]() .
.
Значение функции в точке максимума и минимума называется ее максимумами и минимумами.
Максимумы и минимумы функции называются ее экстремумами, а соответствующее значение аргумента- точка экстремума.
Теорема 1: Пусть функция f(x)
определена и непрерывна на [a, b] и
дифференцируема на (a, b). Если
![]() есть точка экстремума функции, то
есть точка экстремума функции, то
![]() .
.
Пусть х0- точка максимума f(x),
то
при некоторой окрестности точки х0,
тогда в этой точке функция имеет наиб
значение в этой окрестности, а следовательно
по теореме Ферма. ■ Замечание:
1) необходимый признак экстремума
функции, обратное предложение не верно.
Приведем пример на неверно.Пример 1:
![]()
![]() х=0 с одной стороны, но с другой стороны
х=0 не является точкой экстремума функции.
х=0 с одной стороны, но с другой стороны
х=0 не является точкой экстремума функции.
2) в точке экстремума функции ее производная может быть не только равна 0, но и не быть конечной.
Пример 2:
![]()
![]()
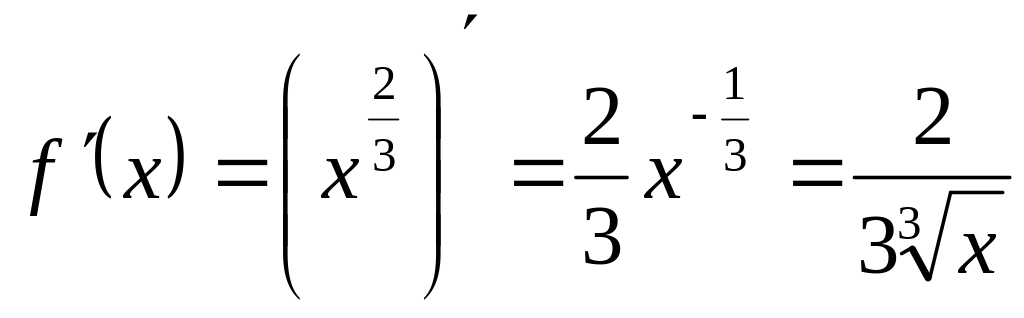
![]() .
(т.е. не существует).Опр. 3: Точки
в которых производная функции равна
нулю называют ее стационарными
точками.Опр. 4 : Точки в которых
производная функции не равна нулю или
не является конечной, называются
критическими точками функции.
Теорему 1 можно обобщить так: любая точка
экстремума функции является ее критической
точкой (но не обратно).Теорема 2:
Пусть функция f(x)
определена и непрерывна на Х, т. е. х0
Х есть критическая точка функции и
на некоторой окрестности этой функции
за искл может быть самой точки х0,
функция имеет производную, которая
слева и справа от точки х0 (в
отдельности) сохраняет постоянный знак,
тогда 1) если
.
(т.е. не существует).Опр. 3: Точки
в которых производная функции равна
нулю называют ее стационарными
точками.Опр. 4 : Точки в которых
производная функции не равна нулю или
не является конечной, называются
критическими точками функции.
Теорему 1 можно обобщить так: любая точка
экстремума функции является ее критической
точкой (но не обратно).Теорема 2:
Пусть функция f(x)
определена и непрерывна на Х, т. е. х0
Х есть критическая точка функции и
на некоторой окрестности этой функции
за искл может быть самой точки х0,
функция имеет производную, которая
слева и справа от точки х0 (в
отдельности) сохраняет постоянный знак,
тогда 1) если
![]() в точке х0 меняет знак с + на –
(при перемещении в положит направлении
оси ОХ), то х0 есть точка максимума
функции; 2) если
в точке х0 меняет знак с – на +, то
х0 –точка минимума; 3) если
в точке х0 функция не меняет знака,
то х0 не является точкой
экстремума.Пусть 1)
в точке х0 меняет знак с + на –.
Пока, что
>0
на (a, х0) следовательно f(x)
возрастает на (a, х0]:
в точке х0 меняет знак с + на –
(при перемещении в положит направлении
оси ОХ), то х0 есть точка максимума
функции; 2) если
в точке х0 меняет знак с – на +, то
х0 –точка минимума; 3) если
в точке х0 функция не меняет знака,
то х0 не является точкой
экстремума.Пусть 1)
в точке х0 меняет знак с + на –.
Пока, что
>0
на (a, х0) следовательно f(x)
возрастает на (a, х0]:
![]()
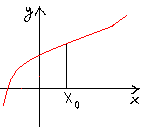
![]() .
.
2) <0 на (х0, b)à f(x) убывает на [х0, b):
![]() [х0,
b)
[х0,
b)
![]()
![]()
![]() -
точка максимума.
-
точка максимума.
3) >0 положительно и слева и справа от точки х0, тогда f(x) возрастает на (a, х0] и [х0, b), т. е. на .■ Теорема является достаточным признаком экстремума функции.
