2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач

Пусть в базисе даны ,

Опр: Векторным произведением векторов и называется вектор , координаты которого находятся по формуле:

Геометрические свойства

1. Если , то ,

Док-во:

Найдем скалярное произведение

,

Аналогично доказывается

2. , ,

Док-во:

Пусть С имеет координаты:

, тогда , ,

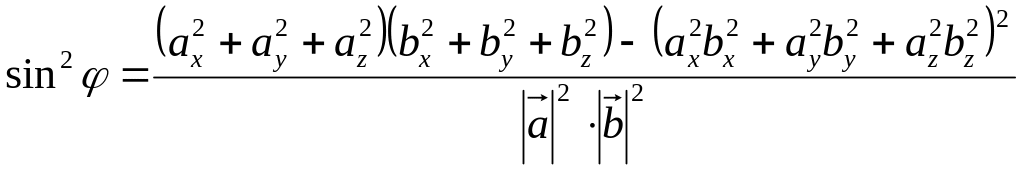
3. того же типа, что , т.е. правая

4.

Док-во:

Из рассмотренных следствий вытекает, что

1) ,

2)

3) - правая

Поэтому векторное произведение векторов имеет геометрический смысл и не зависит от выбора базиса, в котором рассматриваются вектора .

Алгебраические свойства

1. - антикоммутативно

Док-во:

Векторное произведение векторов . Умножим на (–1)

2.

Док-во:

Пусть , , тогда ,

3. - правый дистрибутивный закон

- левый дистрибутивный закон

Док-во:

1 случай: Пусть

Док-ть, что

2 случай:

Применение к решению задач:

М₃ Дано: ∆М₁М₂М₃

М₁

Найти: S∆М₁М₂М₃

(*)

е

Билет №6

1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.

Пусть ф-ия определена в т. и в некот.окр-ти этой т. . Тогда производной наз. ,

Т.: Если существуют , то сущ. в т. производные функций , если в послед.случ.

↓

;

непр., т.к. .Т.о. ↑

Т.: Если в т. и для ф-ии и в т. существ. произв. , то в т. существует произв.ф-ии .

Т.: Если ф-ия определена в некоторой окр-ти т. и возрастает или убывает в этой окр-ти, , то обр.ф-ия имеет произв. в т. , причем .

↓В окр-ти т. в силу возр.(убыв) обр.ф-ия . Если , то , причем в силу возр.(убыв) . Тогда .

↑

2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.

База структуры плоскости Лобачевского состоит из 2 множеств: множества точек и множества прямых. Основные объекты – точки и прямые. Основные отношения:1. Принадлежать. 2. Лежать между. 3. Наложение.Группы аксиом: 1. Аксиомы принадлежности.2. Аксиомы порядка.3. Аксиомы наложения.4. Аксиомы длины. 5L. Аксиома параллельных Лобачевского: Через любую точку, не принадлежащую данной прямой можно провести, по крайней мере, 2 прямые, не пересекающие данную прямую.•Множество , на котором выполняются аксиомы 1-4 групп и 5L называется плоскостью Лобачевского или гиперболической.Аксиомы групп 1-4 те же, что аксиомы евклидовой плоскости в аксиоматике Атанасяна.

НЕОБЯЗАТЕЛЬНО: 1.1. Каковы бы ни были 2 точки прямая, проходящая через эти точки. 1.2. На каждой прямой лежат, по крайней мере 2 точки. Существуют, по крайней мере, 3 точки не лежащие на одной прямой. 2.1. Если , то различные точки одной прямой и В лежит между А и С. 2.2. Каждая т. О прямой разделяет множество остальных точек этой прямой на 2 непустых подмножества, так, что т. О лежит между любыми двумя т. различных подмножеств и не лежит между любыми 2 точками одного подмножества. 2.3.Из 3-х точек на прямой одна и только одна лежит между двумя другими. 2.4. Каждая прямая а разбивает множество остальных точек плоскости на 2 подмножества, так, что любые 2 точки одного и того же подмножества лежат по одну сторону от а, любые 2 точки разных подмножеств лежат по разные стороны от а. 3.1. Каждая фигура равна сама себе. 3.2. (симметричность). 3.3. (транзитивность). 3.4. Если при наложении концы отрезка переходят в концы другого отрезка, то отрезок переходит в отрезок. 3.5. На любом луче от его начала можно отложить отрезок, равный данному и притом единственный. 3.6. Если неразвернутый и , то существует наложение, при котором луч , луч . 3.7. От любого луча в данную полуплоскость можно отложить угол, равный данному неразвернутому углу и притом единственный. 4.1. При произвольно выбранном единичном отрезке, каждый отрезок имеет длину. 4.2. Каково бы ни было положительное действительное число, существует отрезок, длина которого равна d.

• Система аксиом называется непротиворечивой, если из нее нельзя получить 2 утверждения, которые были бы непосредственно противоречивы (т.е. не могут быть одновременно истинными). Другими словами из непротиворечивой системы аксиом логическим путем нельзя получить 2 отрицающих друг друга утверждения.Требование непротиворечивости обязательное требование, так кА нет практического смысла строить противоречивую теорию.Для доказательства непротиворечивости системы аксиом применяют метод интерпретаций. Интерпретация считается построенной, если все аксиомы, проверяемой системы аксиом обращаются в истинные предложения старой теории.Для доказательства непротиворечивости системы аксиом Лобачевского рассмотрим модель Келли-Клейна: Конкретное множество, на объектах которого строится интерпретации К-К это евклидова плоскость , которая построена с помощью аксиоматики Атанасяна.Зафиксируем на некоторый круг , - окружность – граница круга . Точки и прямые на будем обозначать и . Словарь интерпретаций:

• - всякая точка, лежащая внутри круга . Обозначаем: . Из определения следует, что не являются точки окружности и точки внешние для .

• - всякая хорда окружности без ее концов.

•отношение «принадлежать» будем понимать в обычном евклидовом смысле.

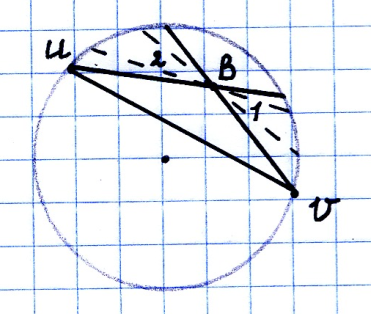
Плоскость - это внутренность круга .Аксиомы 1 группы выполняются для всех точек , а значит и для всех точек, лежащих внутри круга.Проверим аксиому 5E. Пусть дана , . и пересекаются с хордой на окружности в точках окружности на , соответственно, не имеют общих точек. Следовательно, это 2 параллельные .

, проходящие через т. В внутри вертикальных углов 1 и 2 не пересекающие uv и не || ей – это сверх параллельные для uv.

Аксиома 5L выполняется т.к. существует как минимум 2 прямые не пересекающие uv , то и существует бесконечно много таких прямых.

•Отношение «лежать между» для 3-х л-точек одной л-прямой будем понимать в евклидовом смысле. Т.е. А,В,М принадлежат внутренности круга G и , то будем считать, что л-точка М будет лежать между л-точками А и В.Аксиомы 2.1 и 2. 3 выполняются в силу аксиом евклидовой плоскости.Аксиома 2.2. Как по Атанасяну.В этом предложении л-полупрямая Мv с началом в т. М – это пересечение евклидовой полупрямой Мv с внутренностью круга G – это полухорда Mv , (М принадлежит int G, v принадлежит g).2.4. Л-прямая uv разбивает множество не принадлежащих ей точек плоскости L2 на 2 подмножества (л-полуплоскости), так, что л-отрезок, соединяющий точки одной л-полуплоскости не пересекается с л-прямой uv во внутренней точке, а л-отрезок, соединяющий точки разных л-полуплоскостей пересекается с uv во внутренней л-точки. (Верно в силу свойств евклидовой плоскости).3 группа аксиом (наложения):Биективное отображение f круга G в себя называется л-преобразование, если:

1. внутренние т. круга G переходят во внутренние точки, граничные – в граничные.

2. Любая хорда окружности g переходит в некоторую хорду этой же окружности.

3. Сохраняется сложное отношение 4-х точек хорды , т.е 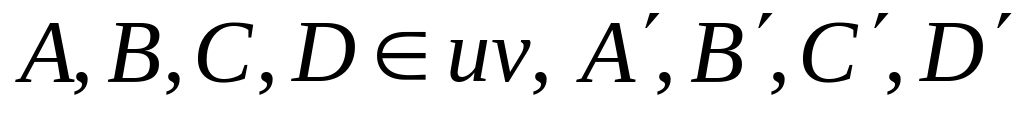- их образы .

Свойства л-преобразований:

1. Множество всех л-преобразований является группой:

2. Л-преобразование сохраняет отношение «лежать между».

Будем называть л-наложением всякое л-преобразование круга G.

Фигура называется равной фигуре если существует наложение при котором .Аксиомы 3 группы выполняются в силу свойств л-преобразований.

Аксиомы 4 группы.Введем понятие л-длины л-отрезка. Пусть дан л-отрезок АВ л-прямой uv , т. u расположена со стороны т.А.•л-длиной будем называть число , где uB,uA, vB, vA евклидовы длины соответственных отрезков.Лемма: л-преобразование сохраняет л-длину л-отрезка, т.е. является л-движением.4.1. При выборе единицы измерения л-отрезков каждый л-отрезок имеет определенную л-длину.При выше описанном выборе точек, следует, что Т.о. устанавливается соответствие мн-ва всех л-отрезков л-плоскости во мн-во положительных действительных чисел. Покажем, что это отображение удовлетворяет аксиомам длины.

Д1: ↓Пусть л-отрезки АВ и СD равны. Значит, сущ-ет л-движение (л-наложение), при котором АВ→СD и при этом сохраняется л-длина л-отрезка, т.е. |AB|л=|CD|л↑

Д2: ↓Пусть . Докажем, что |AB|л=|АМ|л+|МВ|л

, , ↑

Д3: через любую л-точку Р проводим л-прямую (uv). Будем искать на л-прямой такую л-точку Q, чтобы расстояние отрезка PQ равнялось 1.

получили, что т.Q должна делить отрезок uv в данном отношении λ>0. На евклидовой плоскости существует и единственная точка , которая делит данный отрезок в данном отношении. Следовательно, существует и л-отрезок PQ: |PQ|л=1.

4.2. каково бы ни было d из R , d>0, существует отрезок, длина которого равна d. (Док-во как в Д3, только 1 заменить на d).

Мы убедились , что в модели К-К выполняются все аксиомы Атанасяна абсолютной геометрии и аксиома параллельных Лобачевского. Значит модель системы аксиом плоскости Лобачевского построена. Тем самым доказана фундаментальная теорема: Геометрия плоскости Лобачевского на плоскости 1-4 групп и 5L , непротиворечива, если непротиворечива геометрия евклидовой плоскости.

Билет №7