
- •1. Теорема Вейерштрасса о пределе монотонной последовательности.
- •2. Понятие вектора. Линейные операции над векторами и их св-ва.
- •1. Эквивалентность определений предела функции по Коши и Гейне.
- •1. Основные свойства предела функции.
- •1.Сумма, произведение, частное и композиция непрерывных функций.
- •2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.
- •1. Свойства функций непрерывных на отрезке.
- •2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач
- •Геометрические свойства
- •Алгебраические свойства
- •1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.
- •2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.
- •1. Основные теоремы дифференциального исчисления.
- •2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
- •1. Необходимые и достаточные условия возрастания и убывания функции.
- •2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
- •1. Необходимые и достаточные условия локального экстремума функции.
- •2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
- •Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
- •Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
- •1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.
- •Линейные свойства интеграла Римана.
- •Свойства, связанные с неравенствами.
- •1. Достаточное условие существования определенного интеграла.
- •2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
- •1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.
- •2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.
- •2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
- •7.3. Взаимное расположение двух плоскостей.
- •2. Отношение сравнения целых чисел, свойства. Сравнения первой степени.
- •1. Необходимые и достаточные условия дифференцируемости ф-ций комплексной переменной. Понятие аналитической ф-ции в точке и в области.
- •Счетность множества рациональных чисел.
- •1. Несчетность множества точек отрезка [ 0,1 ]
- •2. Кольцо классов вычетов, приведённая система классов вычетов.
- •1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.
- •2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.
- •1. Векторные пространства, простейшие свойства, примеры векторных пространств. Подпространства.
- •Применение гомотетии (подобия) к решению задач на построение (или на доказательство).
- •Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.
- •2. Простые и составные числа. Бесконечность мн-ва простых чисел.
- •1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.
- •1.Классификация движений второго рода плоскости, их применение к решению геом. Задач.
- •2. Системы линейных ур-ий, их виды. Равносильные системы линейных ур-ий. Метод исключения неизвестных, критерий совместности и неразрешимости.
- •2. Изображение пространственных фигур в параллельной проекции.
- •2.Взаимное расположение двух прямых на плоскости Лобачевского.
- •2. Изображение плоских фигур в параллельной проекции.
- •14 Вопрос. Проективная плоскость (пп) и ее модели.
- •19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
7
![]()


П

 лоскость
в пр-ве можно задавать
способами:
лоскость
в пр-ве можно задавать
способами:
1
)
![]() ;
;
![]() ║
║![]() ;
╫
;
╫![]()
2 )
Можно задавать тремя точками не лежащими
на одной прямой:
)
Можно задавать тремя точками не лежащими
на одной прямой:
3) Можно
задавать точкой
(![]() )
и вектором
)
и вектором
![]()
![]() -
наз. нормальным вектором плоскости.
-
наз. нормальным вектором плоскости.
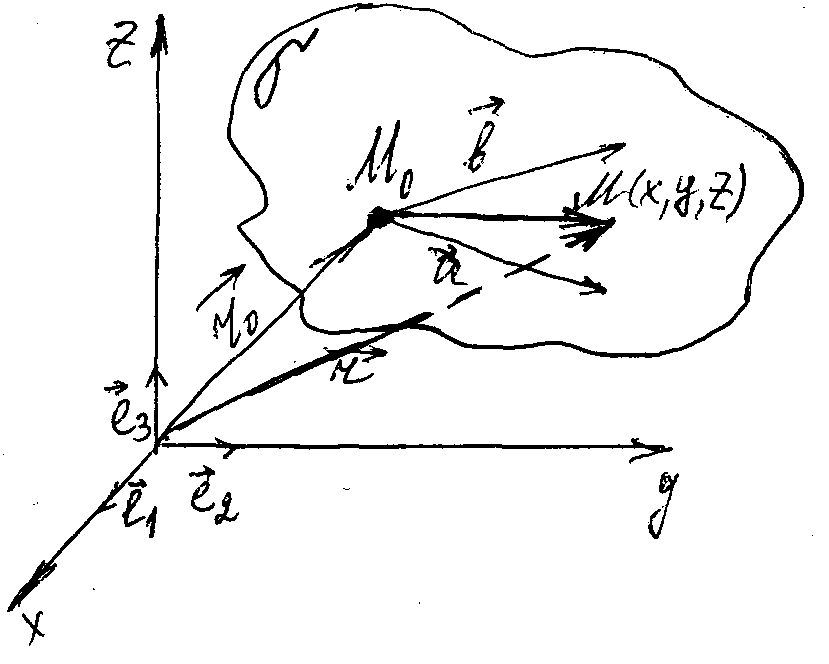
Сущ. и другие способы задания пл-ти. Каждому способу задания пл-ти в пр-ве соотв. некоторое ур-е.
7.1. Уравнение пл-ти проходящей через данную точку параллельно двум не коллинеарным векторам (векторы не лежат на одной прямой и не лежат на //-ых прямых).
Пусть
в
аф.сист.коорд. О![]() пр-ва дана точка
и
даны векторы
пр-ва дана точка
и
даны векторы
![]() //
;
//
;
![]() //
;
╫
.Найти
ур-ие пл-ти
.
//
;
╫
.Найти
ур-ие пл-ти
.
 Пусть
Пусть
![]() -произвольная
точка пр-ва.
-произвольная
точка пр-ва.
![]() ,
когда
,
когда
![]() -
компланарны(т.е. лежат в одной пл-ти или
//-ны одной пл-ти). Но
-
компланарны(т.е. лежат в одной пл-ти или
//-ны одной пл-ти). Но![]()
![]() ,
,
.
Запишем условие компланарности векторов
и
координатной
пл-ти:
,
,
.
Запишем условие компланарности векторов
и
координатной
пл-ти:
 (1)-искомое ур-ие - каноническое
уравнение пл-ти.
(1)-искомое ур-ие - каноническое
уравнение пл-ти.
Вывод параметрических уравнений пл-ти , векторного ур-ия пл-ти .
Пусть
M(x,y,z)-произвольная
точка пр-ва.
-
компланарны, но
╫
(не
коллинеарны). Поэтому их можно принять
за аффинный базис пл-ти
.
Тогда вектор
можно разложить по векторам этого базиса
![]() =
=![]() (2).
(2).
Пусть
![]() ,
,
![]() ,
тогда
=
,
тогда
=![]() ,
,
![]() (3)-
векторное ур-ние.
(3)-
векторное ур-ние.
![]() =
=![]() ;
;
![]() =
=![]() ;
;
![]() ;
;
![]()
Векторное
равенство (3) равносильно двум координатным:
![]() ,
параметрическое
уравнение плоскости,
причём
,
параметрическое
уравнение плоскости,
причём
![]() .
(
.
(![]() -параметры).
-параметры).
7.2.
Теорема 1.
Любая пл-ть
![]() явл.
алгебраической пов-тью I-го
порядка.
явл.
алгебраической пов-тью I-го
порядка.
Док-во.
Пусть пл-ть
задана
в
![]() так:
так:
![]() ,
,
![]() ,
,
![]() ,
╫
,
╫
Возьмём каноническое ур-ие пл-ти в виде определителя: (1),
т.к.
╫
,
Q=![]()
![]()
![]() ,
ранг
,
ранг
![]() (имеет ранг =2), поэтому среди этих
определителей II-го
порядка
(имеет ранг =2), поэтому среди этих
определителей II-го
порядка
![]() ,
,
![]() ,
,
![]() хотя бы один отличен от нуля. Разложим
левую часть определителя (1) по элементам
I-ой
строки I-го
столбца:
хотя бы один отличен от нуля. Разложим
левую часть определителя (1) по элементам
I-ой
строки I-го
столбца:
![]()
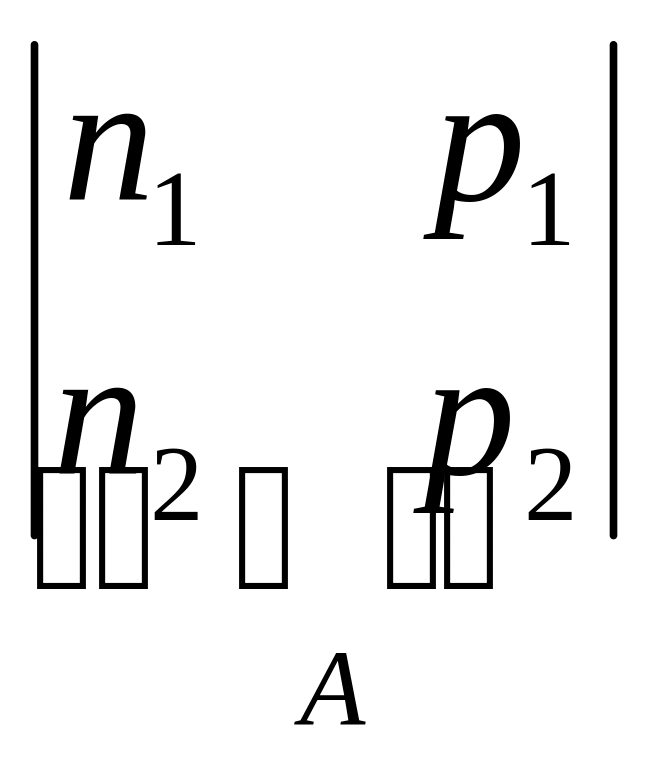 +
+![]()

![]()
 =0;
=0;
![]()
![]()
![]() ;
;
![]() ;
;
![]() (*)- общее ур-ие пл-ти
,
причём
(*)- общее ур-ие пл-ти
,
причём
![]() ур-ие
(*)- это алгебр. ур. I
степени, т.е. оно определяет алг.
поверхность I-го
порядка. Итак, любая пл-ть
- есть алг-ая пов-ть I-го
порядка.
ур-ие
(*)- это алгебр. ур. I
степени, т.е. оно определяет алг.
поверхность I-го
порядка. Итак, любая пл-ть
- есть алг-ая пов-ть I-го
порядка.
Теорема 2 (обратная). Любое ур-ие (*) – I-ой степени определяет пл-ть, т.е. любая линия I-го порядка есть пл-ть (без док-ва).
Из Т.1. и Т.2. , что понятие алг. поверхности I порядка и плоскости совпадает.
7.3. Взаимное расположение двух плоскостей.
Пусть
в аф. сист. коорд.
даны 2 пл-ти
![]() (6) и
(6) и
![]() (7)
(7)
Задание:
Выяснить взаимное расположение этих
плоскостей. Ясно, что если M(x,y,z)![]() корд.
x,y,z
удовл. системе ур-ий (6) и (7). Наоборот,
любое решение системы из ур-ий (6) и (7)
определяет точку принадл. обеим пл-тям
корд.
x,y,z
удовл. системе ур-ий (6) и (7). Наоборот,
любое решение системы из ур-ий (6) и (7)
определяет точку принадл. обеим пл-тям
![]() .
Вывод:
вопрос
о взаимном расположении плоскостей
сводится к решению системы:
.
Вывод:
вопрос
о взаимном расположении плоскостей
сводится к решению системы:![]() ( I
).
( I
).
Запишем
основную и расширенную систему ( I
):
![]() =
=![]()
![]()
![]() ,
,
![]()
![]()
![]()
Пусть
![]() ранг матрицы А (
=
(
)),
ранг матрицы А (
=
(
)),
![]() -
ранг расширенной матрицы
-
ранг расширенной матрицы
![]() (
=
(
)).
(
=
(
)).
Эти
ранги связаны след. отн.
![]()
![]() ,
,
![]()
![]() .
При исследован. сист. ( I
) возм. след. случаи: 1)
.
При исследован. сист. ( I
) возм. след. случаи: 1)
![]() .
В этом случае ур-ия ( I
) лин. независ. и по теореме Кронекера-Капелли
сист. совместна и имеет
.
В этом случае ур-ия ( I
) лин. независ. и по теореме Кронекера-Капелли
сист. совместна и имеет
![]() мн-во реш., сл-но, пл-ти
мн-во реш., сл-но, пл-ти
![]() и
и
![]() имеют
много общих точек, т.е. пересек. по пр.
s.
имеют
много общих точек, т.е. пересек. по пр.
s.
2)
![]() .
По т. Кронекера-Капелли система не
совместна и не имеет решений, и пл-ти не
имеют общих точек, т.е. пл-ти параллельны.
Т.к.
.
По т. Кронекера-Капелли система не
совместна и не имеет решений, и пл-ти не
имеют общих точек, т.е. пл-ти параллельны.
Т.к.
![]() ,
то
,
то
![]() ,
но т.к.
,
но т.к.
![]() ,
,
![]() (условия параллельности плоскостей).
(условия параллельности плоскостей).
3 )
)
![]() .
В этом случае система ур-ий ( I
) линейно зависима, а поэтому пл-ти
и
совпадают. Получаем, что
.
В этом случае система ур-ий ( I
) линейно зависима, а поэтому пл-ти
и
совпадают. Получаем, что
![]() (условия совпадения двух плоскостей).
(условия совпадения двух плоскостей).
ДЛЯ ЗАДАЧ. Уравнение пл-ти проходящей через три данные точки.
Пусть
в
аф.сист.коорд. даны точки
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Составить ур-ие пл-ти
=
.
Составить ур-ие пл-ти
=![]() .
Положим, что вектор
.
Положим, что вектор
![]() ,
,
![]() ,
тогда ур-ие (1) примет вид:
,
тогда ур-ие (1) примет вид:
 (4) – ур-ие пл-ти проходящей через три
данные точки.
(4) – ур-ие пл-ти проходящей через три
данные точки.
У р-ние
пл-ти проходящей через данную точку,
перпен-но данному вектору.
р-ние
пл-ти проходящей через данную точку,
перпен-но данному вектору.
Пусть
в ПДСК
![]() ,
,
,
,
![]() ,
причём
,
причём
![]() .
.
П![]()
![]() .
.
![]() (5).
(5).
Замечание.
Если
задана в ПДСК общим уравнением
:
,
то
![]() - в этом сост. геом. смысл коэф. при
переменных в общем ур-нии пл-ти в ПДСК.
- в этом сост. геом. смысл коэф. при
переменных в общем ур-нии пл-ти в ПДСК.
Билет №14
1.Применение определенного интеграла к вычислению объемов тел. Объем призмы, пирамиды, конуса, шара.
![]()
Предположим, что тело имеет объем и
пусть это тело таково, что все проекции
его сечений, перпендикулярных оси ![]() ,
на плоскость
,
на плоскость ![]() накладываются друг на друга без сдвига.
накладываются друг на друга без сдвига.
Рис.Пусть ![]() - площадь поперечного сечения,
перпендикулярного оси
.
- непрерывна на
- площадь поперечного сечения,
перпендикулярного оси
.
- непрерывна на ![]() .
Разобьем
на частичные
.
Разобьем
на частичные ![]() и пусть
и пусть ![]() .
Тогда из цилиндров высоты
.
Тогда из цилиндров высоты ![]() составятся ступенчатые тела, которые,
с одной стороны, содержат в себе тело
составятся ступенчатые тела, которые,
с одной стороны, содержат в себе тело
![]() ,
а с другой стороны, содержатся в теле
.
Объемы этих ступенчатых тел будут
,
а с другой стороны, содержатся в теле
.
Объемы этих ступенчатых тел будут ![]() и
и ![]() ,
а объем самого тела
будет удовлетворять неравенству
,
а объем самого тела
будет удовлетворять неравенству ![]() .
Т.к.
.
Т.к. ![]() ,
то
,
то ![]() Если,
например, тело есть тело вращения вокруг
оси
криволинейной трапеции, ограниченной
графиком
Если,
например, тело есть тело вращения вокруг
оси
криволинейной трапеции, ограниченной
графиком ![]() ,
в этом случае
,
в этом случае ![]() Прямой
цилиндр – тело, ограниченное цилиндрической
поверхностью, а сверху и снизу – плоскими
фигурами, лежащими в параллельных
плоскостях, причем направляющие
цилиндрической поверхности перпендикулярны
плоскостям.
Прямой
цилиндр – тело, ограниченное цилиндрической
поверхностью, а сверху и снизу – плоскими
фигурами, лежащими в параллельных
плоскостях, причем направляющие
цилиндрической поверхности перпендикулярны
плоскостям.
![]() ;
;
![]() ,
фигура квадрируема.
,
фигура квадрируема. ![]()

![]() – непрерывна на
.
Относительно тела
– непрерывна на
.
Относительно тела ![]() предположим, что все поперечные сечения
этого тела лежат один в другом, если их
спроектировать на одну плоскость.
предположим, что все поперечные сечения
этого тела лежат один в другом, если их
спроектировать на одну плоскость.
Разобьем
точками ![]() И проведем через точки деления поперечные
сечения. Тогда все тело
разобьем на слои
И проведем через точки деления поперечные
сечения. Тогда все тело
разобьем на слои ![]() .
Объем каждого слоя
обозначим через
.
Объем каждого слоя
обозначим через ![]() .
.
![]() .
.
![]() и
и ![]() - наименьшее и наибольшее значения
площади
на
.
Рассмотрим далее совокупность цилиндров
с площадями оснований
и высотой
.
Эти цилиндры образуют ступенчатое тело,
содержащееся в теле
.
Объем этого ступенчатого тела
- наименьшее и наибольшее значения
площади
на
.
Рассмотрим далее совокупность цилиндров
с площадями оснований
и высотой
.
Эти цилиндры образуют ступенчатое тело,
содержащееся в теле
.
Объем этого ступенчатого тела ![]() .
Аналогично совокупность с площадями
оснований
образуют ступенчатое тело, содержащее
в себе тело
.
Объем
.
Аналогично совокупность с площадями
оснований
образуют ступенчатое тело, содержащее
в себе тело
.
Объем ![]() .
Тогда объем самого тела
.
Тогда объем самого тела ![]() .
Суммы, стоящие слева и справа, являются
суммами Дарбу для
.
Суммы, стоящие слева и справа, являются
суммами Дарбу для ![]() на
.
на
.
![]() - существует.
- существует. ![]() =>
интегральные суммы стремятся друг к
другу, т.е.
=>
интегральные суммы стремятся друг к
другу, т.е. ![]() - формула для вычисления объема по
площадям поперечных сечений. Замечание
1. Если тело
не удовлетворяет оговоренным условиям,
т.е. поперечные сечения при проектировании
могут частично накладываться, то в этом
случае тело можно разбить на несколько
тел, удовлетворяющих этим условиям.
Замечание 2. Иногда удобно сечение тела
проводить в некоторой системе координат
плоскостями, перпендикулярными
- формула для вычисления объема по
площадям поперечных сечений. Замечание
1. Если тело
не удовлетворяет оговоренным условиям,
т.е. поперечные сечения при проектировании
могут частично накладываться, то в этом
случае тело можно разбить на несколько
тел, удовлетворяющих этим условиям.
Замечание 2. Иногда удобно сечение тела
проводить в некоторой системе координат
плоскостями, перпендикулярными ![]() или
или ![]() .
.
![]()
2. Система натуральных чисел. Метод матем. индукции. Кольцо цел. чисел. Теорема о делении с остатком для целых чисел.
Под системой натуральных чисел (сист. Пеано) поним. непустое мн-во N, на кот. опр. унарная опер.' («следует за») и выделен эл-т нуль 0, и вып. след. аксиомы:
Р1: 0
N
![]() a
N
(a'≠0)P2:
a,b
N
(a'=b'→a=b)P3:
(акс. индукции)(A
N
0
A
n
N(n
A
→ n'
A))→(A=N).Из
аксиомы индукции вытекает принцип
математической индукции (ПМИ).
a
N
(a'≠0)P2:
a,b
N
(a'=b'→a=b)P3:
(акс. индукции)(A
N
0
A
n
N(n
A
→ n'
A))→(A=N).Из
аксиомы индукции вытекает принцип
математической индукции (ПМИ).
Теорема: Пусть P(n) – некоторый предикат (высказывание) на мн-ве N. Обозн. ч/з A={n N/ P(n)=И}.
↓ Если А уд. акс. индукции, то
n
N
(Р(n)=И).Метод
индукции: Пусть А={![]() |
Р(n)=И}.
|
Р(n)=И}.
1 ш.: Б.И.Проверяется условие, что
![]() ,
т.к. Р(0)=И.2 ш.: П.И.Предполагается, что
,
т.к. Р(0)=И.2 ш.: П.И.Предполагается, что
![]() ,
т.е. предпол., что Р(n)=И.3
ш.: Ш.И.Д-ся, что
,
т.е. предпол., что Р(n)=И.3
ш.: Ш.И.Д-ся, что
![]() ,
т.е. Р(n')=ИЕсли вып-ся все
3 усл., то делается вывод:
n
N
(Р(n)=И). ↑
,
т.е. Р(n')=ИЕсли вып-ся все
3 усл., то делается вывод:
n
N
(Р(n)=И). ↑
Кольцом наз. непустое мн-во С, на кот. опр-ны бинарные операц. «сложение +» и «умножение ∙» эл-тов, удовл. след. услов:
Сист. (А, +) – абелева гр. с нейтр. эл-том 0;
Сист. (А, ∙) – полугруппа ( ∙ - ассоц.);
Умножение дистрибутивно от-но сложения:
a∙(b+c)=a∙b+a∙c (a+b)∙c=a∙c+b∙c.
Теорема о делении с остатком:
Произвольное целое число можно разделить
с остатком на полож. целое число, причем
единственным образом.
![]() ,
q–неполн.част., r-ост.
,
q–неполн.част., r-ост.
↓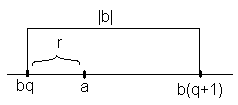 По св-ву Архимеда посл-ть …-2∙b
< -1∙b < 0∙b
< 1∙b < 2∙b
<… бесконечно строго возрастает.
По св-ву Архимеда посл-ть …-2∙b
< -1∙b < 0∙b
< 1∙b < 2∙b
<… бесконечно строго возрастает.
Возьмем наибольшее целое q: bq≤a a < b(q+1).
Положим r = a – bq. Имеем 0 ≤ r < b, т.к. a < bq + b → r = a – bq < b.
Осталось заметить, что a = bq = (a – bq) = bq + r, 0 ≤ r < b.
Докажем единственность разложения. Пусть
—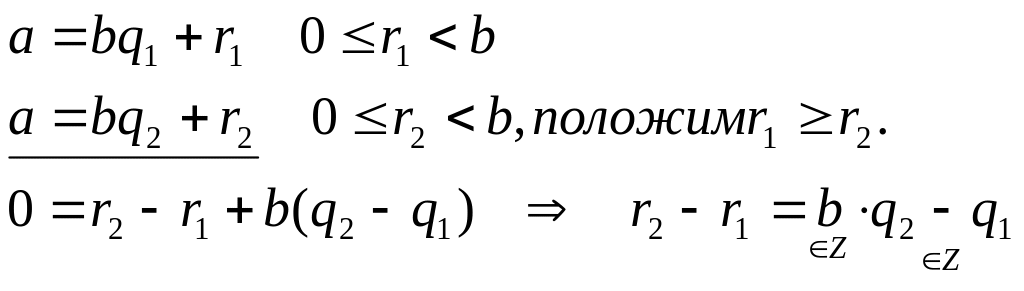
Если r2-
r1>0,
![]()
Билет №15
Сходящийся числовой ряд. Признаки сравнения, Даламбера и Коши сходимости ряда.
Пусть задана некоторая последовательность
чисел ![]() - числовой ряд (1).
- числовой ряд (1). ![]() - члены ряда,
- члены ряда, ![]() - общий член.
- общий член. ![]() - частичная сумма ряда. Если
- частичная сумма ряда. Если ![]() ,
то ряд (1) наз. сходящимся, а число
,
то ряд (1) наз. сходящимся, а число ![]() наз. суммой этого ряда. Если же
наз. суммой этого ряда. Если же ![]() ,
то ряд (1) наз. расходящимся. Пусть дана
некоторая геометрическая прогрессия
,
то ряд (1) наз. расходящимся. Пусть дана
некоторая геометрическая прогрессия
![]() - знаменатель прогрессии,
- знаменатель прогрессии, 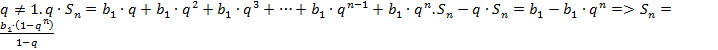 - формула суммы
- формула суммы ![]() членов геометрической прогрессии для
членов геометрической прогрессии для
![]() .
Пусть
.
Пусть ![]() .
В этом случае геометрическая прогрессия
убывающая. Тогда
.
В этом случае геометрическая прогрессия
убывающая. Тогда ![]() сумма членов бесконечно убывающей
геометрической прогрессии. Признак
сравнения двух рядов. Пусть даны два
ряда с неотрицательными членами
сумма членов бесконечно убывающей
геометрической прогрессии. Признак
сравнения двух рядов. Пусть даны два
ряда с неотрицательными членами ![]() и
и ![]() .
И пусть выполняется неравенство
.
И пусть выполняется неравенство ![]() с некоторого номера
с некоторого номера ![]() .
Тогда: 1) если ряд
.
Тогда: 1) если ряд ![]() сходится, то сходится ряд
сходится, то сходится ряд ![]() ;
если ряд
расходится, то расходится и ряд
;
2) если
;
если ряд
расходится, то расходится и ряд
;
2) если ![]() ,
то ряды
и
сходятся или расходятся одновременно.
Признак Даламбера. Пусть члены ряда
положительны,
,
то ряды
и
сходятся или расходятся одновременно.
Признак Даламбера. Пусть члены ряда
положительны, ![]() .
Тогда: 1) если хотя бы начиная с некоторого
номера
.
Тогда: 1) если хотя бы начиная с некоторого
номера ![]() ,
то ряд сходится; если же
,
то ряд сходится; если же ![]() ,
то ряд расходится; 2) если
,
то ряд расходится; 2) если ![]() ,
то при
,
то при ![]() ряд сходится, при
ряд сходится, при ![]() - расходится, а при
- расходится, а при ![]() вопрос о сходимости ряда остается
открытым. Признак Коши. 1 формулировка.
Пусть дан числовой ряд
вопрос о сходимости ряда остается
открытым. Признак Коши. 1 формулировка.
Пусть дан числовой ряд ![]() .
Тогда если: 1) начиная с некоторого номера
выполняется неравенство
.
Тогда если: 1) начиная с некоторого номера
выполняется неравенство ![]() ряд сходится; 2) начиная с некоторого
номера
ряд сходится; 2) начиная с некоторого
номера ![]() ряд расходится.
ряд расходится. ![]() - сходится => данный ряд в силу признака
сравнения сходится.
- сходится => данный ряд в силу признака
сравнения сходится. ![]() не стремится к 0 => в силу необходимого
признака сходимости ряд расходится.
не стремится к 0 => в силу необходимого
признака сходимости ряд расходится.![]() Необходимое условие сходимости ряда:
если ряд сходится, то предел его общего
члена равен 0. 2 формулировка. Если
Необходимое условие сходимости ряда:
если ряд сходится, то предел его общего
члена равен 0. 2 формулировка. Если ![]() ,
то при
ряд сходится, при
ряд расходится.
,
то при
ряд сходится, при
ряд расходится. ![]() .
Тогда по определению предела
.
Тогда по определению предела ![]()
![]()
Векторное, каноническое и общее уравнения прямой в пространстве. Взаимное расположение двух прямых.
Пусть ![]() - прямая в пространстве. Любой ненулевой
вектор, параллельный этой прямой,
называется ее направляющим вектором.
Прямая имеет бесконечное множество
направляющих векторов, любые два из
которых коллинеарны. Все эти векторы,
вместе с нулевым вектором, образуют
одномерное векторное подпространство,
которое называется направляющим
подпространством прямой
.
Положение прямой
в пространстве определяется полностью,
если даны: а) направляющий вектор прямой
и некоторая ее точка; б) две точки прямой;
в) две плоскости, пересекающиеся по
прямой
.
Канонические уравнения прямой. Пусть
в пространстве выбрана аффинная система
координат и в этой системе известны
координаты некоторой точки
- прямая в пространстве. Любой ненулевой
вектор, параллельный этой прямой,
называется ее направляющим вектором.
Прямая имеет бесконечное множество
направляющих векторов, любые два из
которых коллинеарны. Все эти векторы,
вместе с нулевым вектором, образуют
одномерное векторное подпространство,
которое называется направляющим
подпространством прямой
.
Положение прямой
в пространстве определяется полностью,
если даны: а) направляющий вектор прямой
и некоторая ее точка; б) две точки прямой;
в) две плоскости, пересекающиеся по
прямой
.
Канонические уравнения прямой. Пусть
в пространстве выбрана аффинная система
координат и в этой системе известны
координаты некоторой точки ![]() и координаты направляющего вектора
и координаты направляющего вектора ![]() прямой
.
Сначала рассмотрим тот случай, когда
ни одна из координат вектора
прямой
.
Сначала рассмотрим тот случай, когда
ни одна из координат вектора ![]() не равна нулю. Очевидно, точка
не равна нулю. Очевидно, точка ![]() лежит на прямой
тогда и только тогда, когда векторы
лежит на прямой
тогда и только тогда, когда векторы ![]() и
коллинеарны. Вектор
имеет координаты
и
коллинеарны. Вектор
имеет координаты ![]() ,
поэтому для коллинеарности векторов
и
необходимо и достаточно, чтобы их
координаты были пропорциональны, т.е.:
,
поэтому для коллинеарности векторов
и
необходимо и достаточно, чтобы их
координаты были пропорциональны, т.е.:
![]() (1). Эти равенства являются уравнениями
прямой
.
Если одна из координат вектора
равна нулю, например:
(1). Эти равенства являются уравнениями
прямой
.
Если одна из координат вектора
равна нулю, например: ![]() ,
то условие коллинеарности векторов
и
запишется так:
,
то условие коллинеарности векторов
и
запишется так: ![]() (2). Аналогично, если равны нулю две
координаты вектора
,
например:
(2). Аналогично, если равны нулю две
координаты вектора
,
например: ![]() ,
то получаем:
,
то получаем: ![]() (3). В этом случае прямая
параллельна оси
(3). В этом случае прямая
параллельна оси ![]() (если хоть одно из чисел
(если хоть одно из чисел ![]() отлично от нуля) или совпадает с осью
(если
отлично от нуля) или совпадает с осью
(если ![]() ).
Уравнения (1), (2) и (3) называются каноническими
уравнениями прямой. Уравнения прямой,
заданной двумя точками. Пусть в
пространстве выбрана аффинная система
координат и в этой системе известны
координаты двух точек
).
Уравнения (1), (2) и (3) называются каноническими
уравнениями прямой. Уравнения прямой,
заданной двумя точками. Пусть в
пространстве выбрана аффинная система
координат и в этой системе известны
координаты двух точек ![]() и
и ![]() прямой
.
Тогда вектор
прямой
.
Тогда вектор ![]() является направляющим вектором этой
прямой. Т.к. вектор
является направляющим вектором этой
прямой. Т.к. вектор ![]() имеет координаты
имеет координаты ![]() ,
то канонические уравнения прямой
при
,
то канонические уравнения прямой
при ![]() согласно формуле (1) имеют вид:
согласно формуле (1) имеют вид: ![]() .
Если одна из координат вектора
или две его координаты равны нулю, то
для получения канонических уравнений
прямой следует воспользоваться формулами
(2) и (3). Уравнения прямой, заданной двумя
плоскостями. Пусть прямая
является линией пересечения плоскостей
.
Если одна из координат вектора
или две его координаты равны нулю, то
для получения канонических уравнений
прямой следует воспользоваться формулами
(2) и (3). Уравнения прямой, заданной двумя
плоскостями. Пусть прямая
является линией пересечения плоскостей
![]() и
и ![]() ,
которые в аффинной системе координат
заданы уравнениями:
,
которые в аффинной системе координат
заданы уравнениями: ![]() .
(4) Точка
лежит на прямой
тогда и только тогда, когда ее координаты
являются решением системы уравнений
(4), поэтому эта система и является
уравнением прямой
.
Для того чтобы найти каноническое
уравнение прямой, заданной уравнениями
(4), надо знать координаты какой-нибудь
точки
.
(4) Точка
лежит на прямой
тогда и только тогда, когда ее координаты
являются решением системы уравнений
(4), поэтому эта система и является
уравнением прямой
.
Для того чтобы найти каноническое
уравнение прямой, заданной уравнениями
(4), надо знать координаты какой-нибудь
точки ![]() этой прямой и некоторого направляющего
вектора
.
Точку
следует выбрать так, чтобы ее координаты
удовлетворяли системе линейных уравнений
(4). Для нахождения координат направляющего
вектора воспользуемся леммой. Лемма.
Если в аффинной системе координат прямая
задана уравнениями (4), то вектор
этой прямой и некоторого направляющего
вектора
.
Точку
следует выбрать так, чтобы ее координаты
удовлетворяли системе линейных уравнений
(4). Для нахождения координат направляющего
вектора воспользуемся леммой. Лемма.
Если в аффинной системе координат прямая
задана уравнениями (4), то вектор ![]() является направляющим вектором этой
прямой. Параметрические уравнения
прямой. Выберем какую-нибудь аффинную
систему координат и зададим прямую
направляющим вектором
и точкой
.
Точка
пространства лежит на прямой
тогда и только тогда, когда
и
коллинеарны, т.е. когда существует такое
число
является направляющим вектором этой
прямой. Параметрические уравнения
прямой. Выберем какую-нибудь аффинную
систему координат и зададим прямую
направляющим вектором
и точкой
.
Точка
пространства лежит на прямой
тогда и только тогда, когда
и
коллинеарны, т.е. когда существует такое
число ![]() ,
что
,
что ![]() .
Это соотношение в координатах запишется
так:
.
Это соотношение в координатах запишется
так: ![]() ,
или
,
или ![]() .
(5) Эти равенства называются параметрическими
уравнениями прямой, а
- параметром. Их смысл заключается в
следующем: для любого действительного
числа
точка с координатами
.
(5) Эти равенства называются параметрическими
уравнениями прямой, а
- параметром. Их смысл заключается в
следующем: для любого действительного
числа
точка с координатами ![]() ,
удовлетворяющая условиям (5), лежит на
прямой
.
Обратно, если
- точка прямой
,
то всегда найдется такое
,
что
,
удовлетворяющая условиям (5), лежит на
прямой
.
Обратно, если
- точка прямой
,
то всегда найдется такое
,
что ![]() выражаются через
выражаются через ![]() при помощи равенств (5). Взаимное
расположение двух прямых в пространстве.
Зададим в пространстве АСК и
при помощи равенств (5). Взаимное
расположение двух прямых в пространстве.
Зададим в пространстве АСК и ![]() .
Две прямые могут быть либо скрещивающимися,
либо лежащими в одной плоскости
(параллельные, пересекающиеся или
совпадающие). 1)
.
Две прямые могут быть либо скрещивающимися,
либо лежащими в одной плоскости
(параллельные, пересекающиеся или
совпадающие). 1) ![]() и
и ![]() – скрещиваются. Тогда
– скрещиваются. Тогда ![]() - некомпланарны
- некомпланарны  .
2)
и
лежат в одной плоскости. Тогда
- компланарны
.
2)
и
лежат в одной плоскости. Тогда
- компланарны  (*). а)
(*). а) ![]() => их координаты непропорциональны =>
выполняется равенство (*) и 2 и 3 строки
непропорциональны. б)
=> их координаты непропорциональны =>
выполняется равенство (*) и 2 и 3 строки
непропорциональны. б) ![]() ,
но
,
но ![]() .
При этом выполняется условие (*), и в
определителе 2 и 3 строки пропорциональны,
а 1 и 2 непропорциональны. в)
.
При этом выполняется условие (*), и в
определителе 2 и 3 строки пропорциональны,
а 1 и 2 непропорциональны. в) ![]() и
и ![]() выполняется равенство (*), и в определителе
пропорциональны все строки.
выполняется равенство (*), и в определителе
пропорциональны все строки.
Билет №16
1. Ряд Тейлора, достаточное условие разложимости функции в ряд Тейлора. Примеры разложения элементарных функций в степенной ряд.
Пусть функция
определена в некоторой окрестности
точки
и имеет в этой точке производную любого
порядка. ![]() - разложение в ряд Тейлора. Достаточное
условие разложимости. Функция
дифференцируема в некоторой окрестности
точки
сколько угодно раз, причем все производные
- разложение в ряд Тейлора. Достаточное
условие разложимости. Функция
дифференцируема в некоторой окрестности
точки
сколько угодно раз, причем все производные
![]() по модулю в этой окрестности ограничены
одним и тем же числом, т.е.
по модулю в этой окрестности ограничены
одним и тем же числом, т.е. ![]() .
Тогда функция
раскладывается в ряд Тейлора. Воспользуемся
формулой Тейлора
.
Тогда функция
раскладывается в ряд Тейлора. Воспользуемся
формулой Тейлора  .
Надо показать, что
.
Надо показать, что ![]() .
Окрестность точки
обозначим
.
Окрестность точки
обозначим ![]() .
.
![]() .
.
![]() сходится при
сходится при ![]() в силу признака Даламбера => в силу
необходимого условия сходимости ряда
в силу признака Даламбера => в силу
необходимого условия сходимости ряда
![]() при
=>
.
[Признак Даламбера. Пусть члены ряда
положительны,
.
Тогда: 1) если хотя бы начиная с некоторого
номера
,
то ряд сходится; если же
,
то ряд расходится; 2) если
,
то при
ряд сходится, при
- расходится, а при
вопрос о сходимости ряда остается
открытым. Необходимое условие сходимости
ряда. Если ряд сходится, то предел его
общего члена равен 0.] Если
при
=>
.
[Признак Даламбера. Пусть члены ряда
положительны,
.
Тогда: 1) если хотя бы начиная с некоторого
номера
,
то ряд сходится; если же
,
то ряд расходится; 2) если
,
то при
ряд сходится, при
- расходится, а при
вопрос о сходимости ряда остается
открытым. Необходимое условие сходимости
ряда. Если ряд сходится, то предел его
общего члена равен 0.] Если ![]() - разложение по степени
(ряд Маклорена). 1)
- разложение по степени
(ряд Маклорена). 1) ![]() Функцию
Функцию ![]() можно разложить в ряд Маклорена на
можно разложить в ряд Маклорена на ![]() .
Поскольку
.
Поскольку ![]() взята произвольно, то разложение
взята произвольно, то разложение ![]() в ряд Маклорена будет иметь место на
всей числовой прямой.
в ряд Маклорена будет иметь место на
всей числовой прямой. ![]() .
. ![]() - интервал сходимости. 2)
- интервал сходимости. 2) 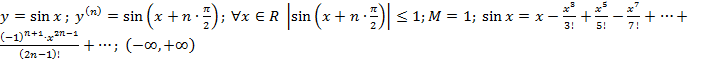 - интервал сходимости.
- интервал сходимости. ![]() - интервал сходимости. 3)
- интервал сходимости. 3) ![]() - биномиальный ряд. (-1;1) – область
сходимости.
- биномиальный ряд. (-1;1) – область
сходимости. ![]() 4)
4) ![]() для
для ![]() .
.
