2. Изображение плоских фигур в параллельной проекции.
Центральное проектирование с несобственным или бесконечно удаленным центром наз. параллельным.
Пусть s - это плоскость оригинала; s¢ - это плоскость проекции; р – прямая, определяющая направление проекции. Пусть плоскость s пересекает s¢ по прямойS.
О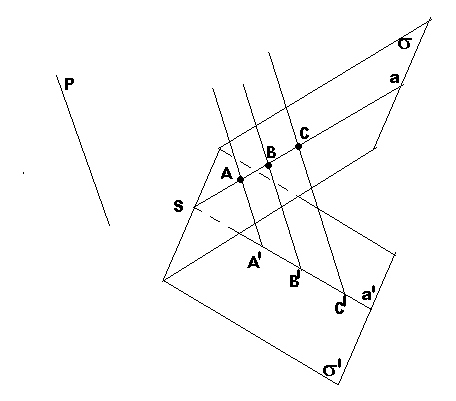
пр
1. Отображение множества точек пр-ва
на плоскость s¢, при
котором любой точки А (В,С) ставится в
соответствие такая т. А¢
(В¢,С¢),
что А¢Îs и АА¢||р
(В¢Îs и ВВ¢||р;
С¢Îs и СС¢||р)
наз. параллельным проектированием,
а т. А¢(В¢С¢)
– наз. параллельной проекцией
т. А на плоскость s¢.
Опр. 2. Пусть Ф – произв. фигура в пр-ве. Найдем проекции всех ее точек на пл-тьs. Параллел. проекции всех точек фигуры Ф образуют некот. фигуру Ф0 на пл-тиs. Фигура Ф0 наз. параллельной проекцией фигуры Ф. Говорят, что фигура Ф0 получена из фигуры Ф параллельным проектированием.Св-ва. Будем считать, что все проектируемые пр. не параллельны прямой р.
10. Параллельная проекция прямой
есть прямая.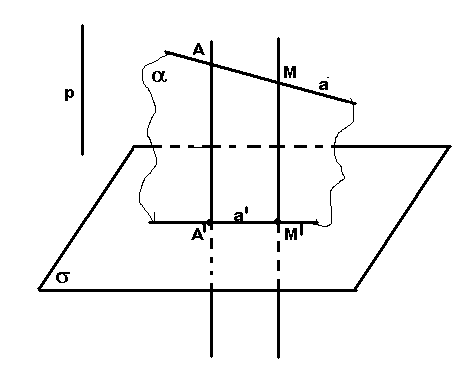
С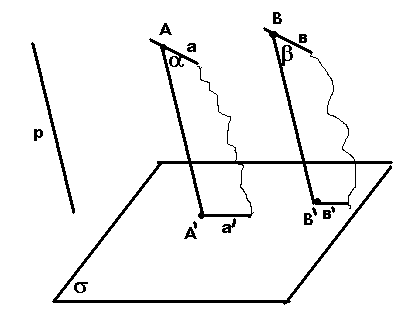
ледствие:
проектирующие прямые всех точек прямойа
лежат в одной плоскости a.
Эта плоскость наз. проектирующей
плоскостью прямой а.
20. Если прямые параллельны, то их параллельные проекции тоже параллельны или совпадают.
3
0.
Проекция отрезка АВ есть отрезок
А0В0-проекции точек А и В.
40. При парал. проектирован.сохр. простое отн. трех точек; в частности, проекция середины отрезка есть середина проекции отрезка.
50. Проекции парал. отрезков параллельны или принадлежат одной прямой.
6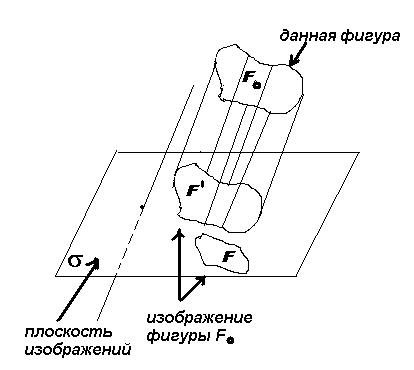
0.
Проекции параллельных отрезков или
отрезков, лежащихна одной прямой,
пропорциональны самим отрезкам.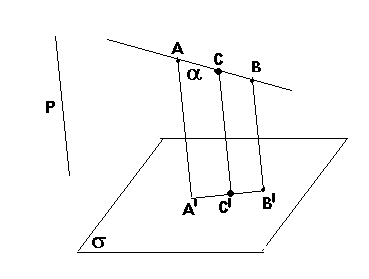
Изображение фигуры.Выберем некоторую пл-тьs и назовем ее пл-тью изображений. Затем возьмем пр.l, пересекающую пл-тьs, и спроектируем данную фигуру F0 на пл-тьs параллельно пр.l. Полученную плоскую фигуру F¢ или любую ей подобную фигуру F на пл-тиs будем называть изображением фигурыF0. Построенное таким образом изображение фигуры соответствует зрительному восприятию фигуры при рассмотрении ее из точки, расположенной далеко от нее. Выбирая разл.пл-ти изображений и разл. направления проектирования (т.е. различные прямые l), будем получать разл. изображения данной фигуры. Обычно берется такое изображение фигуры, кот.яв. наиболее наглядным и удобным для выполнения на нем доп. построений. Это изображение и воспроизводится на чертеже.
Изображение плоских фигур в параллельной
проекции.Опр. Изображением фигуры
в параллельной проекции наз. либо
какая-нибудь параллельная проекция
этой фигуры на плоскость s,
либо фигура, полученная из нее с помощью
преобразования подобия. Построение
изображений фигур основано на свойствах
параллельного проектирования.Требования:
1. верность; 2. наглядность; 3.
простота.Р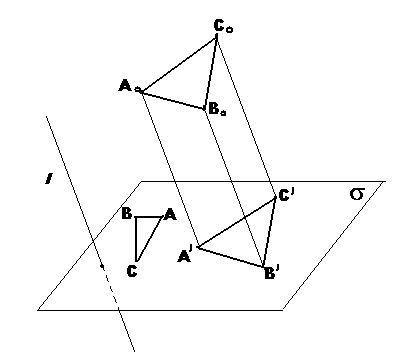
ассмотрим
некоторые примеры изображений плоских
фигур.
Т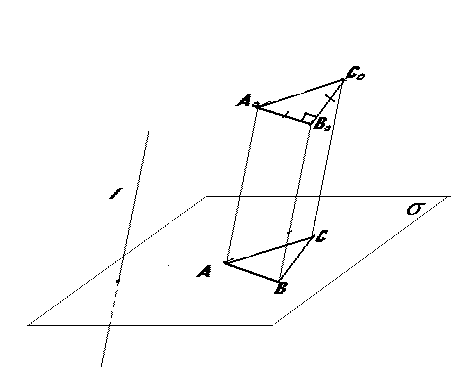
реугольник.
Пусть А0В0С0 –
треугольник, расположенный в пр-ве, АВС
– проекции точек А0В0С0
на пл-тьs.Т.к.
проекция отрезка есть отрезок, то
треугольник АВС (а также любой тр-к
А¢В¢С¢,
подобный тр-ку АВС) является изображением
тр-ка А0В0С0. Вкач-ве
изображения данного тр-ка на чертеже
можно брать произвольныйтр-к. Например,
на рис. изображением прямоугольного
равнобедренного тр-ка А0В0С0.
служит равносторонний тр-к
АВС.Четырехугольник. По теореме об
изобр. плоских фигур (Фигуры F¢
и F,леж. соотв. впл-тяхs¢
и s, наз.
аффинно-эквивалентными, если сущ. аф.
отобр. f:s¢→s,
кот.фигуру F¢
переводит в фигуру F.Теор.:
пусть фигуры F¢
и F лежат соотв. на
непересекающихся пл-тяхs¢
и s. Фигура F
может служить изобр. фигуры F¢т.т.т.,
когда фигуры F¢
и F аффинно-эквивалентны)
любой 4-к пл-тиs,
аф.-эквив. данному 4-ку F¢пл-тиs¢,
может служить его изобр., если пл-тиs¢
и s пересекаются. Для
построения изобр. ABCD
данного 4-ка A¢B¢C¢D¢
в кач-ве вершин А, В и С можно выбрать
произвол. 3 точки, не леж. на одной
прямой.При этом изобр. D
четвертой вершиныD¢опр-ся
однозначно: (A¢C¢,E¢)=(FC,E),(B¢D¢,E¢)=(BD,E),
где Е¢ и Е-точки пересечения прямых А¢С¢, B¢D¢ и AC, BD. (1)
Трапеция. Фигурой, аф.-эквив. трапеции, яв. трапеция, поэтому изобр. трапеции яв. трапеция. Условие (1) в случае трапеции означают, что отн. оснований оригинала равно отн. оснований изображения.
Параллелограмм (вкл. ромб, прямоугольник, квадрат) изобр. в виде параллелограмма. Так как любые 2 пар-мааф.-эквив., то любой пар-м пл-тиизобр. яв. изобр. данного параллелограмма-оригинала.
n-угольник, гдеn>4. Для построения изображения данного n-угольника при n>4 три вершины изобр. можно выбрать произвольно, а остальные вершины находятся построением.
1. Группы. Простейшие свойства и примеры групп. Подгруппы. Гомоморфизм и изоморфизм групп.
Опр: Группой называется непустое мн-во G, на котором определена бинарная операция *, удовл. условиям:
1) бин. операция ассоц. т.е.
2) мн-во сод.
3)
Замечание: 1) Если опер. *=:+ наз. слож., то нейтр. эл-т наз. нулем, обозн. 0, а симметр. эл-т наз. притивопол., обозн. –а. 2) Если опер. *=:∙ наз. умн., то нейтр. эл-т наз. единицей, обозн. 1 или е, а симметр. А наз. обратным, обозн. а-1.
Примеры групп: 1. (Z,+)-аддитивная группа целых чисел; 2. (R,+)-мультипликативная группа положит. действит. чисел; 3. GL(n, F)={A=( ij) | |A| ≠0, ij F}- полн. лин. группа степени n (мно-во всех невырожденных матриц степени n над полем F).
Свойства групп:
1) Закон разрешимости уравнений:
↓ решим уравн. ax=b a-1(ax)=a-1b (a-1a)x= a-1b ex=a-1b x=a-1b ! решение.
2) Закон сокращения
↓ Пусть ab=ac
a-1(ab)=a-1(ac)
(a-1a)b=(a-1a)c
eb=ec
b=c
↓ (a*b)∙(b-1*a-1)=(ассоциат.) a(bb-1)a-1=(ae)∙a-1=a∙a-1=e b-1*a-1=(a*b)-1
3) Законы симметризации:
1. a G ((a')'=a)
2. a,b G ((a*b)'=b'*a')
3. a,b G (a*b=e a=b' b=a')
Опр.: Подгруппой группы (G,*) наз. непустое подмн-во Н G, удовл. усл.:
)
Предложение: Подгруппа явл. группой относительно групповой операции в группе.
Примеры подгрупп:
Пусть заданы гр. (G,∙) и (H,*).
Опр.: Отображение
наз.
гомоморфизмом группы G
в H, если оно сохр. операцию,
т.е.
(образ произведения = произведению
образов).
Пример:GL(n,
F), (R#,
∙)
Свойства:
(образ нейтрального элемента есть
нейтр.)
(образ
симм. равен симметр. образа)
Опр: Биективный гом-зм называется изоморфизмом группы G на H.
Примеры:
G=(Q#, ∙) – мультплик. гр. отличная от нуля рац. чисел.
Свойства:
1. Сва-ва гомоморфизма явл. св-ми изоморфизма.
2. Отнош изоморф-ти явл. отнош. эквивалентности.