Применение гомотетии (подобия) к решению задач на построение (или на доказательство).

Пусть условие задачи на построение разбивается на две независимых части.

Условие - определяет форму фигур.
Условие - определяет размеры фигур.

Тогда эту задачу можно решить методом подобия (гомотетии).

Суть метода: Сначала отказываемся от условия , определяемые размеры искомой фигуры и строим вспомогательную фигуру, удовлетворяющую условию , т.е. подобную искомой. Затем эту вспомогательную фигуру подвергаем преобразованию подобия (гомотетии) так, чтобы выполнялось условие .В результате получим искомую фигуру.

Пример задачи:

Построить треугольник по заданному , по отношению сторон АВ и АС и биссектрисе .

Дано: .

I Анализ.

: дан , : - биссектриса .

Пусть ▲АВС – искомый

AD= , AD- биссектриса.

I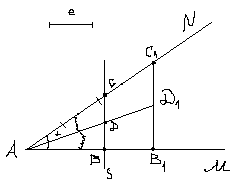 I Построение:

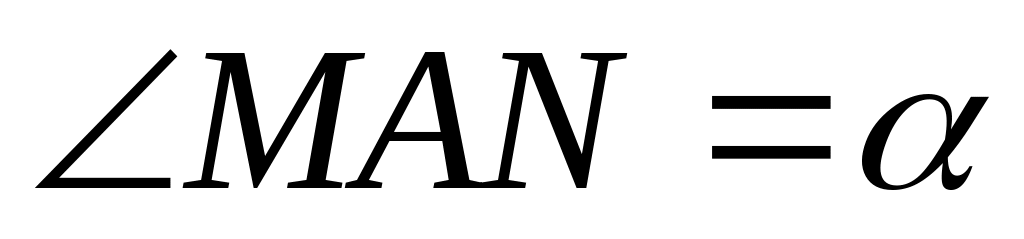
В₁: В_1
,АВ₁=2е.

С₁: С_1
,АС₁=3е.

▲АВ₁С₁
AD₁- биссектриса
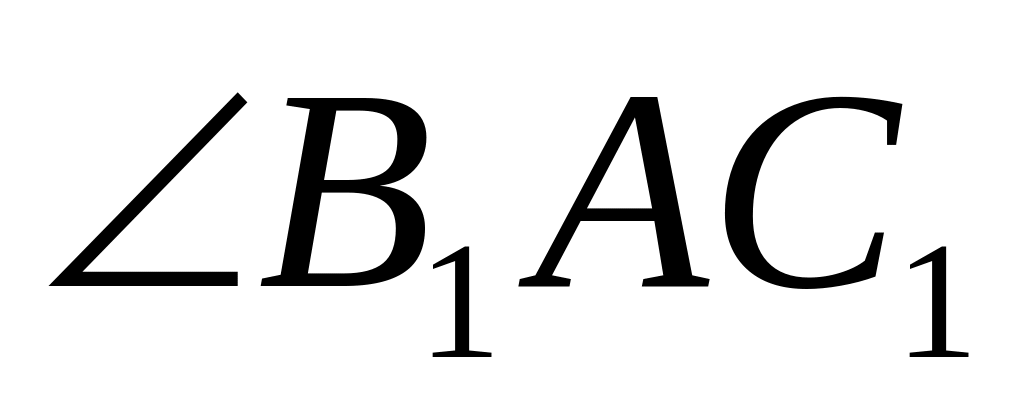
D:D , AD= .
S: D

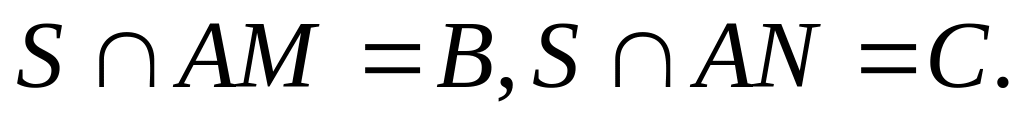
III Доказательство:

▲АВС ~▲А₁ В₁С₁ = =

,AD₁- биссектриса , , AD – биссектриса, AD= .IV Исследование.Задача всегда имеет решение и притом единственное, если .

Билет №22

Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.

Говорят, что преобразование плоскости сохраняет расстояния, если расстояние между любыми двумя точками и плоскости равно расстоянию между их образами и , т.е. . Преобразование плоскости, сохраняющее расстояния, называется движением. Наиболее простым примером движения является тождественное преобразование плоскости, т.е. преобразование, при котором каждая точка плоскости переходит в себя. Рассмотрим другие примеры движений. Пример 1. Возьмем вектор , параллельный плоскости . Каждой точке поставим в соответствие точку так, чтобы . Мы получаем некоторое отображение , которое, очевидно, является преобразованием плоскости . Оно называется параллельным переносом на вектор . Параллельный перенос - преобразование пространства или его части, при котором все точки смещаются в одном и том же направлении на одно и то же расстояние. Пример 2. Поворот. Поворотом на плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении. Пример 3. Центральная симметрия - это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. Теорема. Пусть и - произвольные ортонормированные реперы плоскости . Тогда существует одно и только одно движение, которое репер переводит в репер . При этом движении любая точка с данными координатами в репере переходит в точку с теми же координатами в репере . 1) Докажем сначала, что существует движение, которое репер переводит в репер . Построим отображение следующим образом. Произвольной точке с координатами в репере поставим в соответствие точку с теми же координатами в репере . Ясно, что и . Отображение является взаимно однозначным отображением плоскости на себя, т.е. является преобразованием плоскости . Докажем, что сохраняет расстояния. В самом деле, пусть и - произвольные точки плоскости, которые в репере имеют координаты и . Тогда . Образы и точек и в репере имеют те же координаты: , поэтому и, следовательно, . Таким образом, - движение, которое переводит репер в репер . 2) Докажем теперь, что - единственное движение, которое переводит репер в репер . Допустим, что это не так, т.е. существует другое движение , такое, что . Тогда на плоскости существует такая точка , что образ этой точки в движении не совпадает с образом той же точки в движении . Т.к. и , то , поэтому , т.е. точка равноудалена от концов отрезка . Точно так же можно доказать, что точки и равноудалены от концов отрезка . Таким образом, точки и лежат на серединном перпендикуляре отрезка , т.е. на одной прямой, что противоречит определению репера. Итак, - единственное движение, которое репер переводит в репер . При этом движении точка переходит в точку Будем говорить, что реперы и одинаково ориентированы (противоположно ориентированы), если базисы и одинаково ориентированы (противоположно ориентированы). Говорят, что преобразование точек плоскости сохраняет ориентацию плоскости (меняет ориентацию плоскости), если любой репер и его образ одинаково ориентированы (противоположно ориентированы). Движения, не меняющие ориентацию плоскости, называются движениями первого рода. Лемма 1. Если движение не имеет ни одной инвариантной точки, то оно имеет хотя бы одну инвариантную прямую. Лемма 2. Если движение луч переводит в себя, то это движение либо тождественное преобразование, либо отражение от прямой, содержащей луч. Формулы движений первого рода: Классификация движений первого рода. 1) Движение имеет более чем одну неподвижную точку. Пусть и - две неподвижные точки движения . Тогда луч переходит в себя, поэтому по лемме 2 либо тождественное преобразование, либо осевая симметрия. Но осевая симметрия является движением второго рода, поэтому - тождественное преобразование. 2) Движение имеет только одну неподвижную точку. Выберем ортонормированный репер так, чтобы точка была неподвижной точкой, и запишем аналитическое выражение этого движения (по формулам движения первого рода): . Т.к. не является тождественным преобразованием, то . Это формулы поворота, поэтому - вращение вокруг точки на угол . При либо преобразование - центральная симметрия с центром . Заметим, что если , то не имеет инвариантных прямых (прямую назовем инвариантной, если любая ее точка переходит в эту же точку прямой), а в случае либо - бесконечное множество инвариантных прямых; инвариантными будут те и только те прямые, которые проходят через точку . 3) Движение не имеет неподвижных точек. Согласно лемме 1, существует хотя бы одна инвариантная прямая . Пусть - некоторая точка этой прямой, . Точки лежат на прямой и попарно различны, т.к. не имеет неподвижных точек (если предположить, что точки и совпадают, тогда середина отрезка была бы неподвижной точкой, что невозможно). Выберем ортонормированный репер так, чтобы . Пусть в этом репере точка имеет координаты . Т.к. , то имеет координаты . Допустим, что аналитическое выражение движения в репере имеет вид . Т.к. , то , поэтому формулы движений первого рода принимают вид: (*). Отсюда следует, что - параллельный перенос на ненулевой вектор . Действительно, если - произвольная точка, а - ее образ, то из формул (*) получаем: . Любая прямая, параллельная вектору , является инвариантной прямой параллельного переноса. Других инвариантных прямых нет.