1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.

Теорема(необязательно): Если интегрируемая на , то - непрерывна на .Теорема (о производной определенного интеграла по верхнему переменному пределу): Если непрерывна на , то функция дифференцируема по x и .

Доказательство: ↓ ,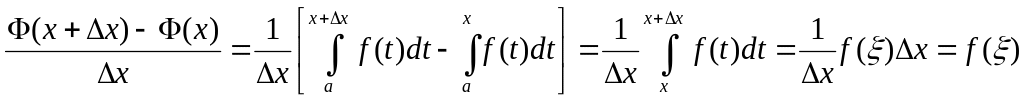

лежит между и . . ↑

• Первообразной от функции в данном интервале называется функция , производная которой равна данной функции: .Формула Ньютона-ЛейбницаТеорема: Если непрерывна на и F некоторая первообразная на Доказательство: В силу утверждения (если непрерывна на первообразная ) является первообразной для : . Пусть , тогда 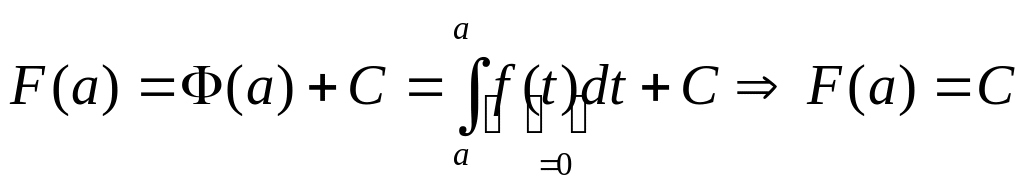, .Пусть , тогда .↑(эта теорема связывает дифф. и интегр. исчисление).

2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.

Пусть F[x]={a₀+a₁x+…+a_nx_n|nN, a₀,…,a_nF} – кольцо многочленов над полем F.Пусть f(x), g(x) - многочлены. Говорят, что g(x) делит f(x), если  h(x)F[x]: f(x)=g(x)∙h(x).Разделить f(x) на g(x) с остатком в кольце F[x], где F-поле, означ. найти мн-н q(x), r(x) F такие, что f(x)=g(x)∙q(x)+r(x), причем r(x)=0 или ст. r(x) < ст. g(x). (*)Теорема (о делении с остатком): Любой многочлен над полем можно разделить с остатком на любой многочлен, отличный от нуля, причем единственным образом.Т.о. если f(x), g(x)0 многочлены над полем F, то  многочлены h(x), r(x) F такие, что: f(x)=g(x)∙h(x)+r(x), где r(x)=0 или cт. r(x)< ст.g(x), причем h(x) и r(x) определены однозначно.

 (теорема о делении с остатком)Сначала докажем существование разлож. (*).Если f(x) =0, то утв. справедливо, разлож. сущ., ибо 0 = 0g(x)+0, ч.т.д.Пусть f(x)≠0 и ст. g(x)> ст.f(x), тогда разложение (*) сущ., ибо f(x)=g(x)∙0+f(x), где h(x)=0, a r(x)=f(x).Т.о., пусть f(x)≠0 и ст. g(x)≤ ст.f(x).Д-ть разложение (*) будем индукцией по n = ст.f(x).Б.И. n=0 => f(x)=a  0, т.к. g(x)≠0 и ст. g(x)≤ ст.f(x)=0, то g(x)=b≠0. Т.к. f-поле, то , ч.т.д., где , r(x)=0. П.И. Утв. (разложение) справедливо для многочленов степени <n , где n>0.Ш.И. Пусть ст. f(x) =n >0, тогда ст. g(x)=m≤n. Пусть .Умножим g(x) на (а₀/b₀)x ^(n-m) и вычтем из f(x): (a) ст. f₁(x)<n.

По П.И. f₁(x) можно разделить на g(x) с остатком:f₁(x)= q(x)h₁(x)+ r(x), где ст. r(x)< ст. g(x) или r(x)= 0, (б)Из (а) и (б)  f(x)= g(x)[(а₀/b₀)x ^(n-m)+h₁(x)]+r(x)=g(x)h(x) + r(x) ч.т.д.

По принципу мат. индукции разложение (*) . Докажем единственность разложения (*).

Пусть f(x) = g(x) h₁(x) + r₁ (x), где r₁(x) = 0 или ст. r₁(x) < ст. g(x) и

f(x) = g(x) h₂(x) + r₂ (x), где r₂(x) = 0 или ст. r₂(x) < ст. g(x).

Вычтем из верхней строки нижнюю.

0=g(x)∙[h₁(x) – h₂(x)] + [r₁(x) – r₂(x)] => r₂ (x) - r₁ (x) = g(x)∙[h₁(x) - h₂(x)].

Если h₁(x)≠ h₂(x)  0,то ст. (r₁- r₂) < ст. g(x) (h₁- h₂), что невозможно  h₁(x)=h₂(x) => r₁(x) - r₂(x)=0 => r₁(x)=r₂(x), ч.т.д. 

Общим делителем мн-нов а(х) и b(х) наз. мн-н g(x): g(x)|a(x), b(x).

НОД многочленов a(x) и b(x) наз. общий делитель, который делится на любой общий делитель мн-нов. Обозн.: (a(x), b(x)) = d(x).

Лемма. Если f(x)=g(x)h(x)+r(x), то (f(x),g(x))=(g(x),r(x)).

Утв. Будет следовать, если пок-ть, что мн-ва общих делителей {f(x), g(x)} и {g(x), r(x)} совпадают.

1. Д-но, если l(x)| f(x), g(x) => l(x)| f(x) – g(x)∙h(x), т.е. l(x)| g(x) и l(x)| r(x).

2. Обратно, если l(x)| g(x), r(x) => l(x)| g(x)∙h(x) + r(x), т.е. . l(x)| f(x), r(x).

Из рав-в а), в) => утверждение, равенство множеств общих делителей. 

Теор. НОД двух мн-нов над полем F существует и равен последнему  0 остатку в посл-ти по алг. Евкл.

Пусть f(x), g(x)F[x], где F – поле, f(x)≠0, g(x)≠0.

По т. о делении с остатком имеем: (разделим f на q с остатком)

f (x)=q(x)q₁(x)+r₁(x) ст. r₁< ст. q

q(x)=r₁(x)q₂(x)+r₂(x) ст. r₂<ст. r₁

т.к. степени остатков убывают, то ч/з конечное число шагов имеем:

r₁(x)=r₂(x)q₃(x)+r₃(x) ст. r₃<ст. r₂

…………..

r_n-2(x)=r_n-1(x)q_n(x)+r_n(x) ст. r_n<ст. r_n-1

r_n-1(x)=r_n(x)q_n+1(x)+0

Для док-ва теор. достаточно пок-ть, что r_n(x)=НОД(f(х), g(х)).

По лемме НОД (f(x), g(x)) = НОД (g(x), r₁(x)) = НОД (r₁(x), r₂(x)) = ….=НОД (r_n-1, r_n) = r_n, т.к. r_n| r_n-1.

Билет №13

1. Площадь криволинейных трапеций

• Любой многоугольник (А), содержащийся в фигуре (Р), называется входящим, а любой многоугольник (В), содержащий фигуру (Р), называется исходящим по отношению к фигуре (Р).

Пусть площадь этих фигур А и В, то А≤В.Рассмотрим множество всех площадей {А}. Это множество ограничено сверху любой площадью В => . Справедливо неравенство (1) , т.к. для {А} число В является верхней гранью, а число является наименьшей из верхних граней. Множество площадей {В} ограничено снизу площадью А и числом по неравенству (1) => (2) , т.к. для множества {В} число является нижней гранью, а число – наибольшей из нижних граней.

• Если точные грани совпадают, , то их общее значение Р называется площадью фигуры (Р), а сама фигура называется квадриремой (3).

Критерий квадрируемости: Фигура квадрируема т.т.т., когда контур, ограничивающий эту фигуру, имеет нулевую площадь.Теорема (формула, выражающая площадь криволинейной трапеции): Если криволинейная трапеция ограничена линиями у=0, х=а, х=b (a<b) и графиком функции y=f(x) непрерывной и неотрицательной на [a, b], то площадь трапеции вычисляется по формуле (4).

Д оказательство: Отрезок [a, b] разобьем на n-частей a=x₀<x₁<…<x_k-1<x_k<…<x_n=b. Через точки деления проведём прямые, параллельные оси ОУ, тогда вся трапеция разобьётся на n-полосок. M_k=max f(x), m_k=min f(x) на [x_k-1, x_k] (k=1, 2,…, n).Эти наибольшие и наименьшие значения существуют на основании теоремы (Теорема Вейерштрасса: Если непрерывна на , то 1) она ограничена на всем отрезке; 2) в некоторых точках этого отрезка достигает своей точной верхней и точной нижней граней).Положим, что ∆x_k= x_k-x_k-1. Рассмотрим прямоугольники с площадями M_k∆x_k и m_k∆x_k. Эти прямоугольники составляют двухступенчатые фигуры, одна из которых является входящей, а другая выходящей по отношению к трапеции. ; .Эти суммы одновременно являются верхней и нижней суммами Дарбу f(x) на [a, b], т.к. функция f(x) по условию непрерывна на отрезке [a, b] , то она интегрируема на этом отрезке. (d = max x_k). d – диметр разбиения.