1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.

О пр: Скалярным произведением 2-х векторов называется число равное произведению длин этих векторов на косинус угла между ними.

φ

Следствия:

1.

2.

Скалярное произведение в координатной форме, его применение.

- ортонормированный базис

Применение:

1.

2.

Алгебраические свойства скалярного умножения векторов.

Теорема:

1⁰.

2⁰.

3⁰. - числовой множитель можно выносить.

4⁰.

↓ 1⁰ непосредственно следует из формулы

2⁰ – из определения скалярного произведения

Выберем - ортонормированный базис и введем в рассмотрение координаты данных векторов

3⁰ Вектор имеет координаты , поэтому

4⁰ Вектор имеет координаты , поэтому ↑

Следствие:

↓ ↑

Геометрические свойства скалярного умножения векторов

1⁰

2⁰ ;

3⁰

↓ 1⁰

↑

↑ 3⁰ ↓

Применение скалярного произведения в школьном курсе математики.

1. Доказать теорему: Если прямая перпендикулярна двум пересекающимся прямым одной плоскости, то она перпендикулярна любой прямой лежащей в этой плоскости (а значит и самой плоскости).

Дано:

a, b

a∩b=p;

s∩α=p

s a, s b.

s t, t α, t – любая прямая.

Док-во:

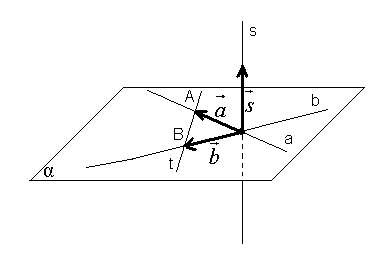
Пусть . Введем векторы ; ясно что

Рассмотрим (вектор является направляющим прямой s). По правилу трех точек

2. Доказать, что диагонали ромба перпендикулярны. Дано: OACB – ромб, . Д-ть:ОС⏊AB. Д-во: , , . Т.о.надо д-ть, что

( )⏊( ). Найдем ( )( ). OACB – ромб⇒OA=OB⇒ . . Значит, ОС⏊AB.

2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.

Пусть F[х] – кольцо полиномов над полем F.Многочлен положительной степени над полем наз. неприводимым (неразложимым), если его нельзя представить в виде произведения двух мн-нов меньшей степени, в противном случае наз. приводимым.Многочлен положит. степени наз. нормированным, если коэффициент при старшей степени равен 1. Заметим, что неприводимость тесно связана с полем.

Примеры: 1) x²+1єR [x]-неприводимое

x²+1єC[x]-приводимое, (x²+1)=(х+i)(x-i)

2) x²-3єQ[x]- неприводимое

x²-3є Q( )[x]-приводимое, x²-3=(x- )(x+ )

Мн-ны f(x) и g(x) положит. ст. наз. взаимно простыми, если НОД (f(x), g(x))=1.Критерий взаимной простоты: Мн-ны f(x) и g(x) над полем положит. ст. взаимно просты   u(x), v(x): 1=f(x)u(x)+g(x)v(x).

Основное св-во неприводимого многочлена над полем: Если неприводимый многочлен над полем делит произведение, то он делит один из множителей.Теор.(о разложении полинома): Мн-н положит. ст. над полем разлагается в произведение нормированных неприводимых мн-нов единствен. образом с точностью до обратимых множителей (эл-тов поля).

↓ Пусть f(x) є F(x), где F – поле и ст. f(x)>0.

Сначала индукцией по ст. n мн-на f(х) док-м существование разложения на неприводимые.

Б.И. ст. f(x)=n=1 => f(x)=ax+b, a≠0 и т.к. f(x) – неприводим, то утв. справедливо.

П.И. Разложение на непривод.  для мн-нов ст. <n, где n>1.

Ш.И. Пусть ст. f(x)=n, n>1. Если f(x)-непривод., то утв. справедливо.

Пусть f(x)-приводим =>  мн-ны a(x), b(x), ст. а(х), ст. b(x)<n и f(x)=a(x)∙b(x).

По П.И. a(x) и b(x) разлагаются на неприводимые.

По принципу мат. индукции утв. справедливо для произвольного многочлена положит. степени, ч.т.д.

Теперь д-м единственность разложения. Заметим, если g(x)-непривод. мн-н, то  c є F: g(x)=c∙p(x), где p(x)-нормированный мн-н (т.е. коэф. при старшей степени равен 1).

Поэтому в силу доказ. первой части => f(x)=c∙p₁(x)…p_m(x) (1), где c є F, р₁,…,р_m-нормир. непривод.

Д-м единственность индукцией по ст. f(x)=n.

Б.И. n=1 f(x)=ax+b= един. образом.

П.И. Утв. справедливо для мн-нов ст. <n, где n>1.

Ш.И. Пусть ст. f(x)=n, n>1. Пусть f(х) имеет другое разложение на непривод.f(x)=d∙q₁(x)…q_k(x), dєF. (2)

Из (1) и (2) => c∙p₁(x)…p_m(x) = d∙q₁(x)…q_k(x).

По осн. св-ву  q_i(x): p₁(x)|q_i(x). (без ограничения общ. положим, что q_i(x)= q₁(x))

Разделим на p₁(x): c∙p₂(x)…p_m(x) = d∙q₂(x)…q_k(x).

По П.И. m=k и p₂=q₂, …, p_m=q_k, c=d, т.е. единственность разложения д-на. ↑

Билет №21