
- •1. Теорема Вейерштрасса о пределе монотонной последовательности.
- •2. Понятие вектора. Линейные операции над векторами и их св-ва.
- •1. Эквивалентность определений предела функции по Коши и Гейне.
- •1. Основные свойства предела функции.
- •1.Сумма, произведение, частное и композиция непрерывных функций.
- •2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.
- •1. Свойства функций непрерывных на отрезке.
- •2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач
- •Геометрические свойства
- •Алгебраические свойства
- •1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.
- •2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.
- •1. Основные теоремы дифференциального исчисления.
- •2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
- •1. Необходимые и достаточные условия возрастания и убывания функции.
- •2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
- •1. Необходимые и достаточные условия локального экстремума функции.
- •2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
- •Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
- •Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
- •1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.
- •Линейные свойства интеграла Римана.
- •Свойства, связанные с неравенствами.
- •1. Достаточное условие существования определенного интеграла.
- •2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
- •1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.
- •2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.
- •2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
- •7.3. Взаимное расположение двух плоскостей.
- •2. Отношение сравнения целых чисел, свойства. Сравнения первой степени.
- •1. Необходимые и достаточные условия дифференцируемости ф-ций комплексной переменной. Понятие аналитической ф-ции в точке и в области.
- •Счетность множества рациональных чисел.
- •1. Несчетность множества точек отрезка [ 0,1 ]
- •2. Кольцо классов вычетов, приведённая система классов вычетов.
- •1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.
- •2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.
- •1. Векторные пространства, простейшие свойства, примеры векторных пространств. Подпространства.
- •Применение гомотетии (подобия) к решению задач на построение (или на доказательство).
- •Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.
- •2. Простые и составные числа. Бесконечность мн-ва простых чисел.
- •1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.
- •1.Классификация движений второго рода плоскости, их применение к решению геом. Задач.
- •2. Системы линейных ур-ий, их виды. Равносильные системы линейных ур-ий. Метод исключения неизвестных, критерий совместности и неразрешимости.
- •2. Изображение пространственных фигур в параллельной проекции.
- •2.Взаимное расположение двух прямых на плоскости Лобачевского.
- •2. Изображение плоских фигур в параллельной проекции.
- •14 Вопрос. Проективная плоскость (пп) и ее модели.
- •19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
2. Изображение пространственных фигур в параллельной проекции.
К изображению пространственных фигур в геометрии предъявляются требования:
1) верность; 2) наглядность; 3) простота выполнения.
Изображение считается верным, если оно передает одну из возможных проекций оригинала для выполнения этого требования достаточно при построении изображения использовать свойства параллельного проецирования и теоремы Польке – Шварца и Польке .С учетом 2 и 3 требования из возможных проекций оригинала выбирается та, которая наилучшим образом соответствует требованиям наглядности и содержит меньше дополнительных построений.
Опр. 1: Проекцией пространственной фигуры называется совокупность проекции всех ее точек.
Для получения проекции той или иной пространственной фигуры в общем случае не всегда нужно проецировать все ее точки. Например, для многогранника достаточно найти проекцию всех его вершин, а тогда будут определены проекции всех его ребер, граней, т. е. вся проекция многогранника. Далее будем считать, что плоскость проекции - плоскость чертежа, а проецируемая фигура расположена произвольно в пространстве и направлена параллельного проецирования произвольное. Поэтому можно говорить о произвольной параллельной проекции пространственных фигур.
Опр. 2: Канонической проекцией пространственной фигуры называется та проекция при которой изображение проекции наглядное и более простое.
Теорема Польке – Шварца: Любой плоский 4-угольник A1B1C1D1 вместе с его диагоналями может
служить изображением тетраэдра ABCD произвольной формы.
○![]() -
диагонали,
-
диагонали,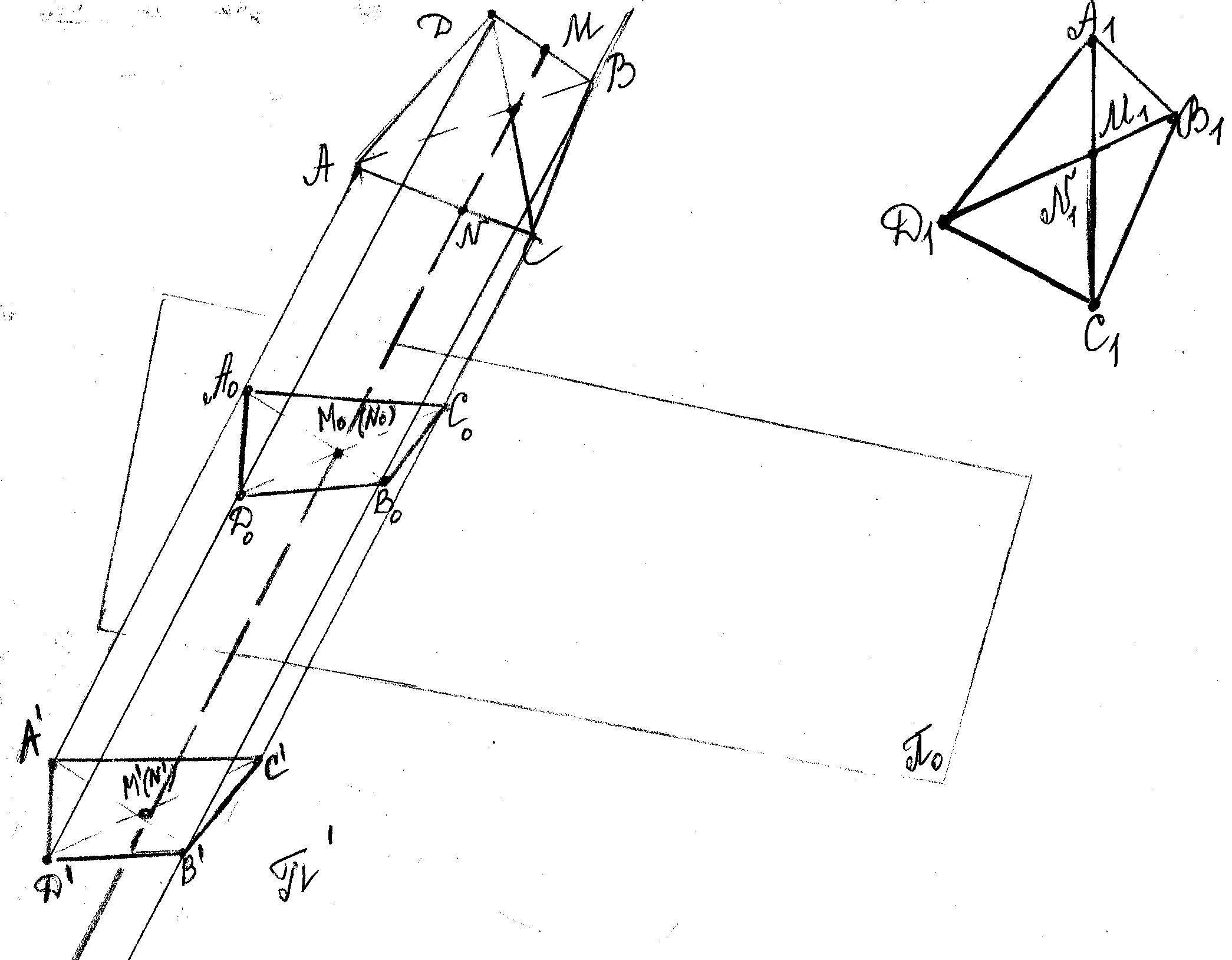
![]() .
Пусть ABCD произвольный
тетраэдр. На ребре BD
построим точку М:
.
Пусть ABCD произвольный
тетраэдр. На ребре BD
построим точку М:![]() .На
ребре АС построим точку М:
.На
ребре АС построим точку М:
![]() .
Примем прямую MN за
направление проецирования. А плоскость
проекций
.
Примем прямую MN за
направление проецирования. А плоскость
проекций
![]() возьмем так, что MN
.
Найдем ортогональную проекцию тетраэдра
на пл.
,
для этого найдем …..Получим 4-угольник
A0B0C0D0
вместе с диагоналями, который является
ортогональной проекцией тетраэдра на
пл.
.
По свойствам параллельного проецирования
имеем, что
возьмем так, что MN
.
Найдем ортогональную проекцию тетраэдра
на пл.
,
для этого найдем …..Получим 4-угольник
A0B0C0D0
вместе с диагоналями, который является
ортогональной проекцией тетраэдра на
пл.
.
По свойствам параллельного проецирования
имеем, что
![]() ,
но по условию
,
но по условию
![]() (1). Аналогично,
(1). Аналогично,
![]() ,
но по условию
,
то
,
но по условию
,
то
![]()
![]() (2). Получили, что для 4-уг. A1B1C1D1
и A0B0C0D0
выполняется условие теоремы*:Если два
4-угольника таковы, что их диагонали
делятся в точке пересечения в отношениях
одинаковых для обоих 4-угольников, то
один из них (любой) является ортогональной
проекцией некоторого 4-угольника
подобного другому.
(2). Получили, что для 4-уг. A1B1C1D1
и A0B0C0D0
выполняется условие теоремы*:Если два
4-угольника таковы, что их диагонали
делятся в точке пересечения в отношениях
одинаковых для обоих 4-угольников, то
один из них (любой) является ортогональной
проекцией некоторого 4-угольника
подобного другому.
Чтобы принять следствие теоремы*: если основанием прямой призмы служит один из двух 4-угольников, удовлетворяющих теореме*, то среди плоских сечений такой призмы всегда можно указать такой 4-угольник, который будет подобен второму; продолжим прямые AA0, BB0, CC0, DD0 и примем их за ребра прямой призмы с основанием A0B0C0D0 и к этой призме применим следствие: Всякую прямую треугольную призму можно пересечь плоскостью так, что в сечении получиться треугольник любой наперед заданной формы. Среди плоских сечений этой призмы всегда найдется такой 4-угольник A’ B’ C’ D’ который будет подобен A1B1C1D1-данный 4-угольник.
Найденный 4-угольник A’
B’ C’
D’ с одной стороны
подобен A1B1C1D1,
с другой стороны является вместе с
диагоналями параллельной проекцией
тетраэдра на плоскость
![]() .
Следовательно, данный 4-угольник A1B1C1D1
является изображением тетраэдра ABCD.
Под изображением пространственной
фигуры понимается либо ее проекция на
плоскость проекции, либо фигура подобная
ей.●
.
Следовательно, данный 4-угольник A1B1C1D1
является изображением тетраэдра ABCD.
Под изображением пространственной
фигуры понимается либо ее проекция на
плоскость проекции, либо фигура подобная
ей.●
Изображение призмы и пирамиды в параллельной проекции.
Построение изображения призм и пирамид в параллельной проекции, опирается на теорему Польке- Шварца и свойства параллельного проецирования. Построение этих тел начинается с построения изображения оснований.Пример: Построить прямую пятиугольную призму.
1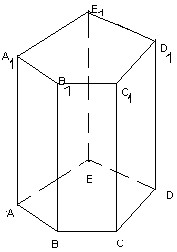 .
Строим АВСДЕ.
.
Строим АВСДЕ.
2. т. к. призма прямая, то через вершину проводим прямые – боковые ребра, параллельные вертикальному обрезу листа (для наглядности).
Соединим вершины верхнего основания
Изображение вершины пирамиды берется произвольно, но более наглядным изображением пирамиды считается такое, когда изображение высоты пирамиды параллельно боковому краю листа.
Пример: Построить правильную 4-угольную пирамиду SABCD.
ABCD-произвольный параллелограмм.
О=
 ,
прямая s параллельна краю
чертежа
,
прямая s параллельна краю
чертежаБ
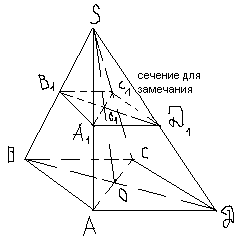 ерем
точку
ерем
точку
 ,
S – вершина.
,
S – вершина.Проводим ребра.
Замечание: При построении изображения усеченных пирамид нужно следить за тем, чтобы продолжения боковых ребер пересекались в одной точке- вершине полной пирамиды, то начинать надо с построения полной пирамиды.
Изображение кругового цилиндра в параллельной проекции.
Нижнее основание цилиндра изображается в виде произвольного эллипса. Из центра этого эллипса откладывается в любом направлении отрезок произвольной длины, получим изображение центра верхнего основания цилиндра. Строим эллипс, равный начерченному, с центром в точке, полученной параллельным переносом из первого эллипса. Затем проводится общая касательная к этим эллипсам.
П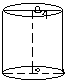 ри
изображении прямого кругового цилиндра
основания (эллипсы) для наглядности
проводят так, чтобы большая ось каждого
из них была перпендикулярна боковому
краю листа, а центры этих эллипсов лежали
на общем перпендикуляре к большим осям.
В этом случае крайние боковые образующие
пройдут через концы большой оси каждого
из эллипса.
ри
изображении прямого кругового цилиндра
основания (эллипсы) для наглядности
проводят так, чтобы большая ось каждого
из них была перпендикулярна боковому
краю листа, а центры этих эллипсов лежали
на общем перпендикуляре к большим осям.
В этом случае крайние боковые образующие
пройдут через концы большой оси каждого
из эллипса.
Изображение конуса вращения в параллельной проекции.
О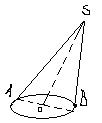 снование
конуса изображается в виде произвольного
эллипса независимо от формы конуса
вращения. Проекцию S-его
вершины можно выбрать произвольно,
затем строится касательная из точки S
к эллипсу.
снование
конуса изображается в виде произвольного
эллипса независимо от формы конуса
вращения. Проекцию S-его
вершины можно выбрать произвольно,
затем строится касательная из точки S
к эллипсу.
М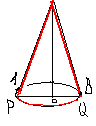 ожно
установить, что точки касательной А и
В конт. образующие SA и SB
не являются диаметрально противоположными.
Более наглядной проекцией конуса
является такая, когда большая ось
основания параллельна нижнему краю
листа, а высота конуса перпендикулярна
большой оси.
ожно
установить, что точки касательной А и
В конт. образующие SA и SB
не являются диаметрально противоположными.
Более наглядной проекцией конуса
является такая, когда большая ось
основания параллельна нижнему краю
листа, а высота конуса перпендикулярна
большой оси.
Замечание : При построении осевых сечений конуса, т. е. плоскостями, проходящими через ось нужно помнить, что крайняя образующая не является диаметрально противоположной.
Изображение шара в ортогональной проекции.
Обычно изображение шара строят только в ортогональной проекции, т. к. в этом случае проекция шара есть круг, а очерковая линия есть окружность, но это изображение являясь верным не является наглядным. Чтобы изображение шара стало наглядным, на чертеже строят проекции некоторых точек и линий, принадлежащих поверхности шара.Опр. 1: Полюсами шара называют точки пересечения поверхности шара с ее осью.Осью поверхности шара называют вертикальную прямую, проходящую через центр шара.Опр.2: Экватором шара называется линия пересечения поверхности шара с горизонтальной плоскостью, проходящей через центр шара.
Опр. 3: Параллелями шара называются линии пересечения поверхности шара с горизонтальными плоскостями, параллельными плоскости экватора.
Опр. 4: Меридианами шара называются линии пересечения поверхности шара с плоскостями, проходящими через ось шара.
До ортогонального проектирования шара
мысленно отмечаем на поверхности шара
экватор и полюс, затем наклоняем плоскость
экватора или ось шара, чтобы она не была
горизонтальной, но ось шара была
параллельной профильной плоскости
проекции, тогда экватор ортогонально
проецируется в эллипс, отношение осей
которого определяет наклон плоскости
экватора к плоскости чертежа. Изображенный
экватор, позволяет найти проекции
полюсов. Для рисунка 1. С целью поиска
проекции п олюсов,
рассмотрим профильную плоскость, которая
проходит через ось шара и перпендикулярна
плоскости проекции, затем повернем ее
вокруг линии пересечения этой плоскости
с плоскостью чертежа до совмещения с
плоскостью чертежа, тогда –
олюсов,
рассмотрим профильную плоскость, которая
проходит через ось шара и перпендикулярна
плоскости проекции, затем повернем ее
вокруг линии пересечения этой плоскости
с плоскостью чертежа до совмещения с
плоскостью чертежа, тогда –![]() профильная
проекция экватораДля рисунка 2.
Проводим
профильная
проекция экватораДля рисунка 2.
Проводим
![]() ,
,
![]() -
профильная проекция оси шара. NS-фронтальная
проекция оси шара. N-северный
полюс, S – южный полюс.
-
профильная проекция оси шара. NS-фронтальная
проекция оси шара. N-северный
полюс, S – южный полюс.
Замечание: оказывается северный и
южный полюса шара можно построить и не
используя профильную проекцию. Рассмотрим
треугольники ONN1 и
D1DO
они равны: ON1=D1O=R,
![]() как острые углы с соответственно
перпендикулярными сторонами
ON==DD1,
NN1=OD.Поэтому,
зная экватор шара можно построить полюсы
без профильной проекции.Пусть: 1. AB,
CD–оси экватора.2. строим
DD1-касательная к
экватору в т.D. DD1
параллельна AB. 3.строим
N, S. ON=OS=DD1.
Наоборот, если известны Nи
S, то можно построить
экватор без профильной проекции.
как острые углы с соответственно
перпендикулярными сторонами
ON==DD1,
NN1=OD.Поэтому,
зная экватор шара можно построить полюсы
без профильной проекции.Пусть: 1. AB,
CD–оси экватора.2. строим
DD1-касательная к
экватору в т.D. DD1
параллельна AB. 3.строим
N, S. ON=OS=DD1.
Наоборот, если известны Nи
S, то можно построить
экватор без профильной проекции.
Построение:1.![]() ,
2.ON1, 3.
,
2.ON1, 3.![]() ,
4.проводим DD1
параллельно AB., 5.OC=OD,C
NS.
6.AB и CD-оси
экватора, по ним строим экватор.
,
4.проводим DD1
параллельно AB., 5.OC=OD,C
NS.
6.AB и CD-оси
экватора, по ним строим экватор.
О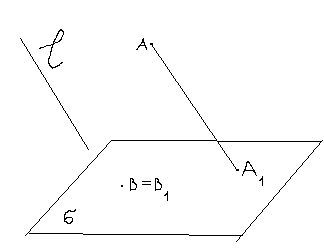 пр.
5: Точка называется заданной, если
заданы проекция точки и проекция ее
основания на основную плоскость. Опр.
6: Изображение называется полным,
если все точки являются заданными
(примеры полных изображений см. в
лекциях). Опр.7:Задачи на построение
на проекционном чертеже, в которой
требуется определить общие элементы
данных фигур, называются позиционными.
Для решения позиционных задач
достаточно, чтобы чертеж был полным. К
позиционным задачам относятся все
задачи на построение сечений многогранников,
цилиндров, конусов. Эти сечения строят
обычно двумя способами: 1. Способ следов.
2.Способ внутреннего проецирования.
пр.
5: Точка называется заданной, если
заданы проекция точки и проекция ее
основания на основную плоскость. Опр.
6: Изображение называется полным,
если все точки являются заданными
(примеры полных изображений см. в
лекциях). Опр.7:Задачи на построение
на проекционном чертеже, в которой
требуется определить общие элементы
данных фигур, называются позиционными.
Для решения позиционных задач
достаточно, чтобы чертеж был полным. К
позиционным задачам относятся все
задачи на построение сечений многогранников,
цилиндров, конусов. Эти сечения строят
обычно двумя способами: 1. Способ следов.
2.Способ внутреннего проецирования.
С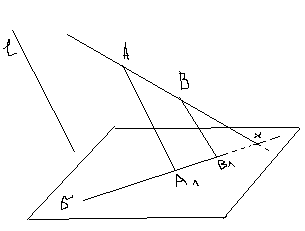
 пособ
следов. Под следом секущей пл.
понимают прямую по которой пл.
пересекается с какой-либо гранью
многогранника, чаще всего с плоскостью
нижнего основания многогранника или
основной плоскостью. Этот способ
основан на двух задачах: Построить
точку пересечения (след), заданной
прямой, с основной пл.
.Прямая
АВ задана, значит известна ее проекция
на плоскость
(А1В1). Ясно, что Х=АВ
пособ
следов. Под следом секущей пл.
понимают прямую по которой пл.
пересекается с какой-либо гранью
многогранника, чаще всего с плоскостью
нижнего основания многогранника или
основной плоскостью. Этот способ
основан на двух задачах: Построить
точку пересечения (след), заданной
прямой, с основной пл.
.Прямая
АВ задана, значит известна ее проекция
на плоскость
(А1В1). Ясно, что Х=АВ![]() А1В1.Частный случай: Если
АВ//
,
то решения (следа) нет.
А1В1.Частный случай: Если
АВ//
,
то решения (следа) нет.
2. Секущая пл. определяется тремя заданными точками А(А1), В(В1), С(С1). Построить след этой плоскости в основной плоскости . Х=АВ А1В1. Х= ВС В1С1 ,р=(ХУ).
Способ внутреннего проецирования.Очень
часто след секущей плоскости оказывается
за пределами чертежа в этом случае проще
использовать внутреннее проектирование.В
случае призм и цилиндров применяют
способ // внутреннего проектирования.
Пирамиды, конусы - центральное внутреннее
п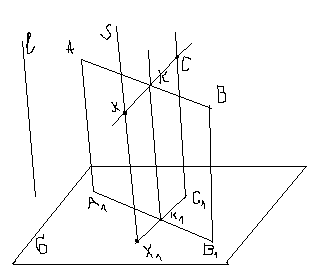 роектирование
(принимая за центр проецирования вершину
пирамиды, конуса).
роектирование
(принимая за центр проецирования вершину
пирамиды, конуса).
Этот способ основан на двух задачах:1. (для // внутреннего проектирования ). Секущая пл. задана А(А1), В(В1),С(С1). Дана пр. S-проецирующая соответствующая т. Х1. Построить т. Х=S . Построение: 1. К1=А1В1 С1Х1 2. К1 А1В1 К АВ, К1К//АА1 К=АВ К1К
3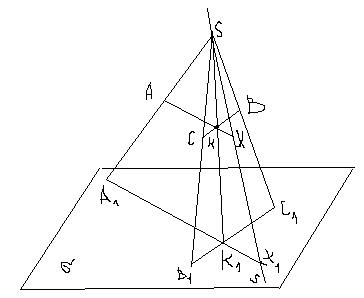 .Х1
С1К1Х
СК,
Х
SХ=S
СК.
4. Х- искомая точка.
.Х1
С1К1Х
СК,
Х
SХ=S
СК.
4. Х- искомая точка.
2. (для центрального внутреннего проецирования).
Даны S-центр внутреннего проецирования, центральные проекции А1, В1,С1 на основную пл. точек А, В, С секущей плоскости . S- произвольная проецирующая прямая: S=SX1, X1 . Построить точку Х пересечения пл. с прямой S.
Построение:
1. К1=В1С1 А1Х1
2. К1 В1С1 К ВС, К SK1, К= SK1 ВС
3.Х1 А1К1Х АК, Х SХ=S АК.
4. Х- искомая точка.
точек А, В, С. о проецирования, центральные проекциинего проектирования. случае проще использовать внутреннее проектирование.
Билет №26
1. Отношение делимости в кольце целых чисел. Наибольший общий делитель и наименьшее общее кратное двух нат. чисел. Алгоритм Евклида. Критерий взаимной простоты двух нат. чисел.
Опр. Целое число а делит число b, если такое целое число сZ, такое что b=а·c (b-делимое, а-делитель, с-полное частное). (обозн. а|b).
Пример: 36|3, т.к. такое целое число 12, что 36 можно представить 36=3·12.
Св-ва:
Отношение делимости рефлексивно: аZ а|а (любое целое число делится само на себя).
Отношение делимости транзитивно: целых а,в,сZ а|в и в|с а|с.
Если а|b (-а)|b, a|(-b), (-a)|(-b).
Отношение делимости сохраняется при изменении знака делимого и делителя.
Если а|с и b|с, то сумма или разность тоже делится на с: а|с и в|с(ав)|с
Если а делится на с и b целое число, то произведение a·b тоже делится на с: a|c и bZ (a·b)|c
Если а делится на с и b не делится на с, то сумма или разность не делится на с
(a|c и b не |с(ab) не |с).
Нуль делится на любое целое число неравное нулю (а|0, аZ).
Любое целое число делится на 1(1|a, аZ).
9. Если а≠0, то не такого цел. числа q, что а=0·q, это значит, что а не равное нулю не делится на 0.
Опр. НОД чисел а1,…,аn, n≥2 наз. наибольший их общий делитель.
(НОД – общий делитель, кот. делится на любой общий делитель).
Лемма: Если a=bq+r, то НОД(a,b)=НОД(b,r).
Алгоритм Евклида
Пусть а, bN, b0. Осуществим деление с остатком по следующей схеме (делитель делим на остаток).
a =bq0+r1 0r1<|b|
b=r1q1+r2, 0r2<|r1|
r1=r2q2+r3, 0r3<|r2| (*)
……………………
r n-2=rn-1qn-1+rn 0r1<|rn-1|
rn-1=rnqn
По лемме: (a,b)=(b,r1)=(r1,r2)=…=(rn-1,rn)=rn.
Заметим, что процесс послед. деления по алгоритму Евклида конечен, т.к. конечна убывающая посл-ть.
НОД сущ. всегда. Он равен последнему остатку ≠0 по алгоритму Евклида.
Критерий НОД: Общий делитель d чисел а и b яв. НОД u,v Z: d=au+bv.
Опр. Если (а,в) = 1, то числа а и b явл. взаимно простыми.
Критерий взаимной простоты двух натуральных чисел.
Для того чтобы числа а и b были взаимно простыми, необходимо и достаточно, чтобы существовали такие целые числа u,v, что au+bv=1. (1)
↓(=>). Если числа а и b взаимно просты, то (а, b)=1. Тогда по т-ме (если d – НОД чисел а и b, то такие целые числа u,v, что au+bv=d) такие целые числа u,v, что au+bv=1.
(<=). Пусть такие целые числа u и v, что имеет место равенство (1), и пусть (а, b)=d. Тогда (согласно св-ву 4 делимости) из (1) следует, что 1|d. Значит, d=1, т.е. числа а и b взаимно просты.↑
Опр. НОК чисел а и b наз. общее кратное, которое делит любое общее кратное этих чисел.
Обозн.: НОК[a,b] или [a,b].
Теорема. НОК двух чисел равен отношению произведению этих чисел и НОД, т.е. .
↓Пусть d=(a,b). Тогда a=a1d, b=b1d и (a1,b1). Пусть с-общее кратное а и b: c=aq=bt=a1dq=b1dt => a1q=b1t. Т.к. а1 и b1 – вз/прост. => b1|q, т.е. q=b1s. Т.о. c=a∙b1∙s= ∙s, s≥1. ↑
