1. Свойства функций непрерывных на отрезке.

Ф-я f(x) назыв. непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка Х.

Теорема Больцано-Коши: Если функция f(x) непрерывна на [a, b] и на концах отрезка принимает значение разных знаков, например, , , то такая что .

Отр. [a, b] разделим на 2 равные части точк. , если , то т-ма док-на.

Пусть .Из двух половин отрезка [a₁, b₁] выберем ту на концах которых функция принимает значения разных знаков, т. е. пусть .

Отрезок [a₁, b₁] разделим пополам точкой , если - то теорема док-на. Пусть . Выберем [а₂, b₂] на концах которой функция принимает значения разных знаков, т. е. . Разделим отрезок пополам точкой и т. д.

При неограниченном продолжении этого процесса получим, что или не сущест .

Получим последовательность отрезков [a₁, b₁], [a₂, b₂], . . ., [a_n,b_n], … обладает свойством . Эта последовательность является стягивающейся, т. к.

1. [a_n+1,b_n+1] [a_n,b_n]; 2. Длины этих отрезков равны: при n→∞, тогда по т-ме Кантора о стягив-ся отрез. такая что , (в пределе n)■

Г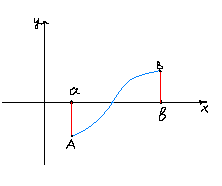 еометрический смысл теоремы.

Если на непрерывной кривой есть точка ниже и выше оси ОХ, то есть точка в которой график пересекает ось ОХ. Такая точка может быть не одна.

Пример на применение этой теоремы:Эта теорема может служить для обоснования приближ.реш-ия скалярн.ур-ий вида f(x)=0. Находят отрезок [a, b] , в кот.корень единств. На концах кот.f принимает значения противопол.по знаку и т.с- всего одна. Далее применяется процесс деления отр.пополам. Кол-во таких шагов опред-ся степенью точности нахождения данного корня. Найти х, с точностью до 0,1 .

.

Функция f(x) строго возрастает как сумма возрастающей функции. А возрастающая функция каждое свое значение принимает в единственной своей точке, в нашем случае 0.

Разделим отрезок точкой пополам. , . , , . , . ,

или , тогда .

Т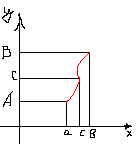 еорема 1: Если функция f(x) непрерывна на [a, b] и на концах отрезка принимает разные значения: где , то такая что .

(вторая теорема Больцано-Коши или теорема о промежуточных значениях непрерывной функции).

Теорема 1 есть частный случай теоремы 2, когда А<0, В>0.

Геометрическое представление.

Теорема 2: Если функция f(x) непрерывна на [a, b], то она ограничена на отрезке [a, b] и имеет на нем наибольшее и наименьшее значение. (теорема Больцано-Вейерштрасса) .

Т.Вейерштрасса: Если ф-ия непрер. на [a,b], то она ограничена на этом отрезке и в некоторых точках этого отрезка достигает своих точной верхней и точной нижней граней, т.е.

↓1) Докажем, что ф-ия ограничена на [a,b]. Предположим противное. Пусть - неограниченна на [a,b]. Тогда Последовательность точек лежит на [a,b]. ( ) ограничена⇒в силу теоремы Больцано-Вейерштрасса сущ. последоват. , кот. сходится в некот.т. , тогда в силу непрер. ф-ии f⇒ , т.е. ( )- явл-ся сходящейся, а поэтому она ограничена, что противоречит нер-ву

2) Докажем, что Отметим, что - существует в силу 1) теоремы. . Докажем от противного. Предположим, что на отрезке нет точки, в которой достигается, т.е. ф-ию 0 , опред.для всех точек отр. , т.к. - непр., то и - непрер., а поэтому в силу 1)части теоремы эта ф-ия явл.огранич. на этом отрезке, т.е. 0 Получили противоречие, т.к. получили верх.границу , кот. меньше, чем верх.грань M, чего быть не может. ↑