
- •1. Теорема Вейерштрасса о пределе монотонной последовательности.
- •2. Понятие вектора. Линейные операции над векторами и их св-ва.
- •1. Эквивалентность определений предела функции по Коши и Гейне.
- •1. Основные свойства предела функции.
- •1.Сумма, произведение, частное и композиция непрерывных функций.
- •2. Симметрические многочлены от нескольких переменных. Основная теорема о симметрических многочленах. Формулы Виета.
- •1. Свойства функций непрерывных на отрезке.
- •2. Векторное ум. Двух векторов трёхмерного евклидового пространства, его свойства и применение к решению задач
- •Геометрические свойства
- •Алгебраические свойства
- •1. Производная суммы, произведения, частного и композиции функции. Произв. Обратной функ.
- •2. Система аксиом плоскости Лобачевского,д-во ее непротиворечивости.
- •1. Основные теоремы дифференциального исчисления.
- •2. Смеш. Произ. 3 в-ров 3-х мерного Евклидова пр-ва. Его св-ва и прим. К реш. Геомет. Задач.
- •1. Необходимые и достаточные условия возрастания и убывания функции.
- •2. Многочлены от одной переменной над полем действительных чисел. Сопряженность мнимых корней, описание неприводимых многочленов.
- •1. Необходимые и достаточные условия локального экстремума функции.
- •2. Прямая на плоскости как линия первого порядка.Взаим.Распол. Двух прямых.
- •Различные способы задания прямой (направляющим вектором и точкой) и соответствующие им уравнения.
- •Взаимное расположение 2-х прямых на плоскости, заданных общими уравнениями.
- •1. Линейные св-ва опред.Интеграла и св-ва,связанные с неравенствами.
- •Линейные свойства интеграла Римана.
- •Свойства, связанные с неравенствами.
- •1. Достаточное условие существования определенного интеграла.
- •2. Эллипс,гипербола,парабола. Вывод канон.Ур-ия, изучение формы.
- •1. Теорема дифференц. Опред. Интеграла по верхнему пределу.Формула Ньютона-Лейбница.
- •2. Отношение делимости в кольце многочленов от одной переменной над полем. Нод двух многочленов. Алгоритм Евклида.
- •2. Плоскость как поверхность первого порядка. Взаимное расположение двух плоскостей.
- •7.3. Взаимное расположение двух плоскостей.
- •2. Отношение сравнения целых чисел, свойства. Сравнения первой степени.
- •1. Необходимые и достаточные условия дифференцируемости ф-ций комплексной переменной. Понятие аналитической ф-ции в точке и в области.
- •Счетность множества рациональных чисел.
- •1. Несчетность множества точек отрезка [ 0,1 ]
- •2. Кольцо классов вычетов, приведённая система классов вычетов.
- •1. Скалярное умножение двух векторов трехмерного евклидова пространства, его свойства и применение к решению геометрических задач.
- •2. Неприводимые многочлены над полем. Разложение многочлена в произведения неприводимых множителей и его единственность над полем.
- •1. Векторные пространства, простейшие свойства, примеры векторных пространств. Подпространства.
- •Применение гомотетии (подобия) к решению задач на построение (или на доказательство).
- •Классиф. Движений первого рода плоскости, их применение к решению задач по геометрии.
- •2. Простые и составные числа. Бесконечность мн-ва простых чисел.
- •1. Тригон. Форма комп. Числа. Формула Муавра. Корни n – ой степени из комплексного числа.
- •1.Классификация движений второго рода плоскости, их применение к решению геом. Задач.
- •2. Системы линейных ур-ий, их виды. Равносильные системы линейных ур-ий. Метод исключения неизвестных, критерий совместности и неразрешимости.
- •2. Изображение пространственных фигур в параллельной проекции.
- •2.Взаимное расположение двух прямых на плоскости Лобачевского.
- •2. Изображение плоских фигур в параллельной проекции.
- •14 Вопрос. Проективная плоскость (пп) и ее модели.
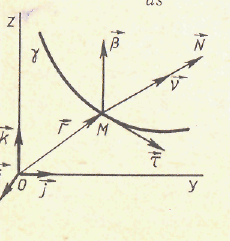
- •19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
19. Кривизна и кручение кривой в трехмерном евклидовом пространстве.
Опр. Пусть элементарная линия задана параметрическими уравнениями
 х
= x(
t
)
х
= x(
t
)
у = y(t) (1) или векторным →r = →r (t) (2), где t I
z = z(t)
линия называется гладкой линией класса Ck (где k >= 3), если функции x( t ), y(t), z(t) имеют в промежутке I имеют непрерывные производные до порядка k включительно и
[x\(t)]2+[y\ (t)]2+[z\(t)]2 0 или r\(t) 0 при t I
Опр. Линия наз-ся гладкой, если все покрывающие её линии наз-ся гладкими.
Например: окружность не является элементарной линией, но является гладкой, т.к. окружность можно покрыть двумя полуокружностями, каждая из которых является гладкой кривой.
Гладкую элементарную линию можно задать в естественной параметризации.
П усть
в ПДСК О ijk
усть
в ПДСК О ijk
0 : x=x(s)
y=y(s) (3) →r = →r (s) (4), где s – естественный параметр или длина дуги.
z=z(s)
![]() -
- единичный вектор касательной, т.к.|
единичный вектор касательной, т.к.|![]() |=1,
то
|=1,
то
![]()
Опр. Вектор
![]() =
=
![]() называется вектором
кривизны линии
в точке М,
называется вектором
кривизны линии
в точке М,
![]()
а его длина | |= | |= k — кривизной линии в точке М. На всей линии кривизна является функцией параметра s.
Из определения
-ет,
что кривизна кривой в точке характеризует
скорость поворота касательной на дуге
кривой
от точки с параметром s
до точки с параметром s+![]() s.
s.
![]()
Опр. Прямая, определенная (М, ) наз-ся главной нормалью кривой в точке М.
Опр.
![]() =
/
|
|
- наз-ся единичным вектором главной
нормали.
=
/
|
|
- наз-ся единичным вектором главной
нормали.
= | |*
= ; | |= k .
= k* - первая формула Френе.
Опр. Рассмотрим вектор
![]() =
=
![]()
| |=| |*| | sin900=1
(
,
),
(
,
,
)
– правая тройка, как
![]()
Вектор наз-ся единичным вектором бинормали кривой в точке М.
Опр. Репером Френе наз-ся совокупность
точки М и ортонормированного базиса
,
![]() ,
.
,
.
Координатные плоскости имеют свои названия
(М, , ) — соприкасающаяся плоскость;
(М, , ) — нормальная плоскость;
(М, , ) — спрямляющая плоскость.
При перемещении точки М по линии перемещается и репер RM, Учитывая это, репер RM часто называют подвижным репером линии .
М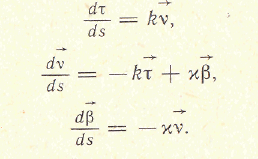 ожно
доказать, что вектор
ожно
доказать, что вектор
Вторая формула Френе
Третья формула Френе

0
Q =
=
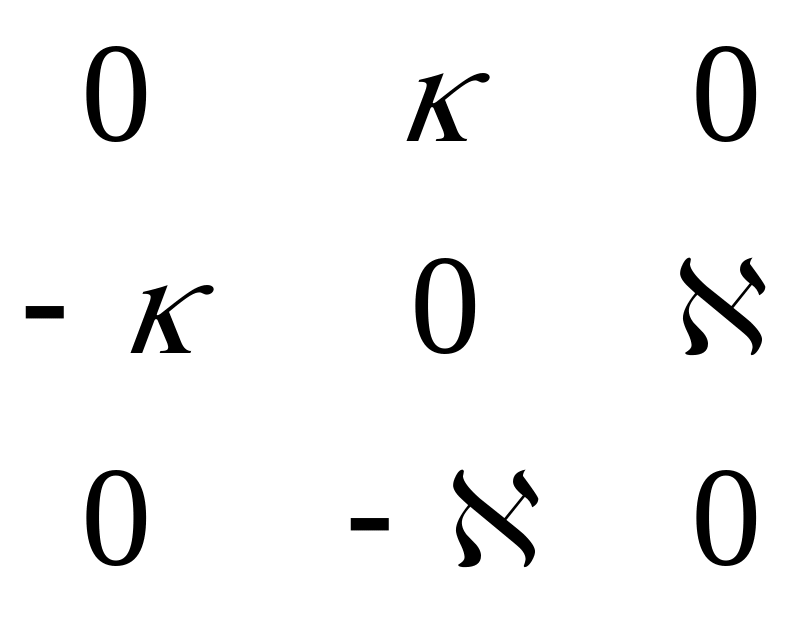 матрица
кососимметрическая.
матрица
кососимметрическая.
О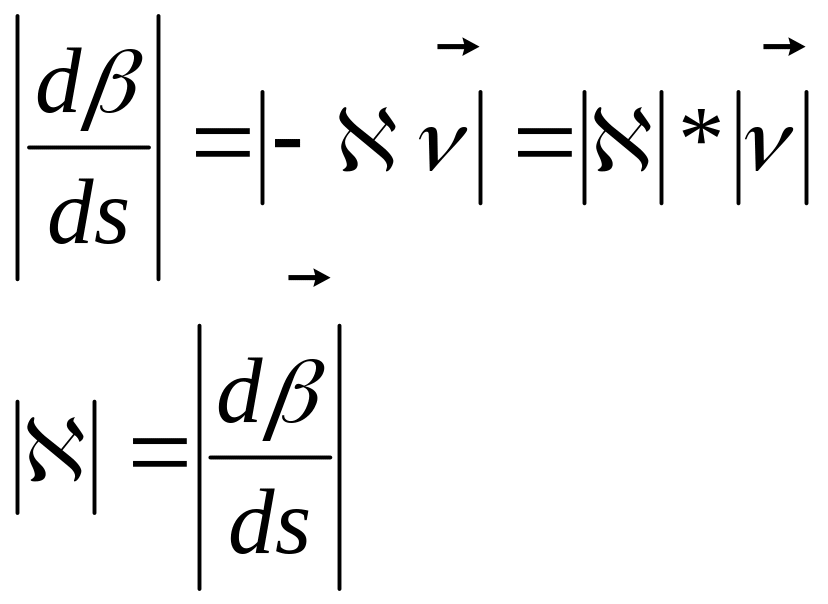 пр.Коэффициент
пр.Коэффициент
![]() в третьей формуле Френе наз-ся кручением
кривой
в точке М.
в третьей формуле Френе наз-ся кручением
кривой
в точке М.
кручение характеризует скорость поворота бинормали
на кривой
при переходе от точки с параметром s
до точки с параметром s+
s,
т.к.
![]() .
.
19.3. Кривизна и кручение винтовой линии. Применение винтовой линии в технике.
Пусть линия
задана уравнением
![]() ,
где t-
произвольный параметр,
меняющийся в промежутке I.
,
где t-
произвольный параметр,
меняющийся в промежутке I.

х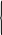 = a cos t
= a cos t
у = a sin t (1)
z = bt
где а = const > 0, b = const О и t изменяется в некотором промежутке I.
Уравнения (1) определяют элементарную линию. Она называется обыкновенной винтовой линией. Как показывают уравнения (5), винтовая линия — гладкая линия класса С .
Введем на линии естественную параметризацию s и допустим, что функция s=h(t) определяет замену параметра.
Если
![]() -
уравнение линии
в естественной параметризации, то
-
уравнение линии
в естественной параметризации, то
![]() -
то же уравнение, что и уравнение
-
то же уравнение, что и уравнение
![]() ,
поэтому
,
поэтому
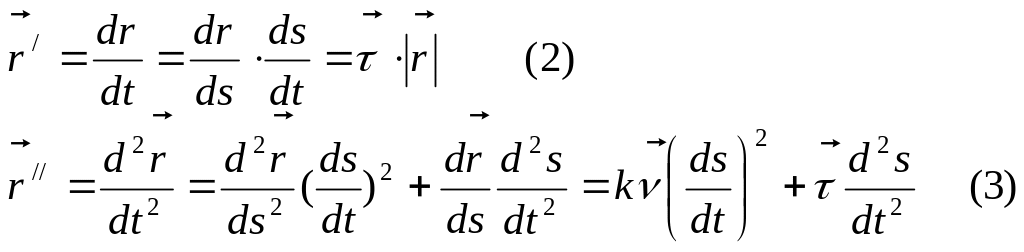
Мы замечаем, что вектор
![]() параллелен соприкасающейся плоскости.
параллелен соприкасающейся плоскости.
Имеем:
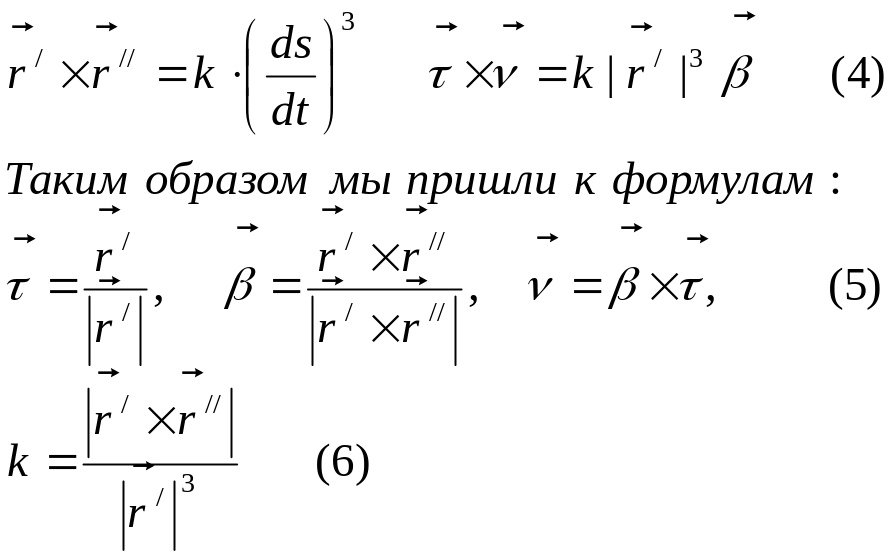
Осталось получить формулу для вычисления
кручения
.
С этой целью найдем разложение вектора
![]() по координатным векторам репера (
,
,
),
используя формулу (3) и формулы Френе.
Нас будет интересовать коэффициент при
векторе
:
по координатным векторам репера (
,
,
),
используя формулу (3) и формулы Френе.
Нас будет интересовать коэффициент при
векторе
:

20. Первая квадр. форма поверхности и её прим. Понятие о внутренней геометрии поверхности
Пусть дана гладкая поверхность, заданная
векторным уравнением
![]() (1) и параметрическими уравнениями:
(1) и параметрическими уравнениями:
 ,
где
,
где
![]() - элементы поверхности
- элементы поверхности
![]()
![]()
![]()
![]()
Полагаем, что
 ,
тогда получаем, что
,
тогда получаем, что
![]()
Опр-е:
![]() называется первой квадратичной
функцией.
называется первой квадратичной
функцией.
![]()
![]() ,
следовательно – эта квадратичная форма
положительно определённая.
,
следовательно – эта квадратичная форма
положительно определённая.
Длина дуги и кривой на поверхности:
Пусть на
![]() задана
гладкая линия:
задана
гладкая линия:
![]() ,
,
![]()
![]() при
непрерывны,
дифференцируемы и
при
непрерывны,
дифференцируемы и
![]()
![]() одновременно, тогда, если точки
одновременно, тогда, если точки
![]() ,
,
![]() ,
то длина дуги
,
то длина дуги
![]() вычисляется
по формуле:
вычисляется
по формуле:
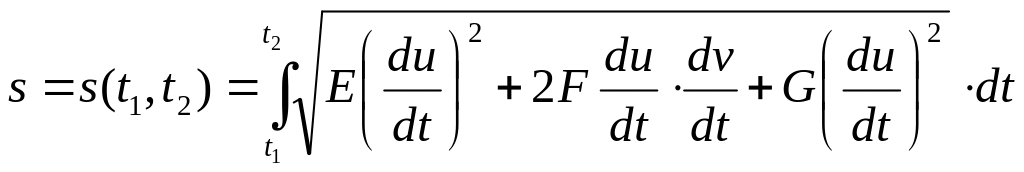
Угол между двумя кривыми на поверхности:
Составим параметрическое уравнение сферы, обозначив u – долготой, v – широтой.
![]()
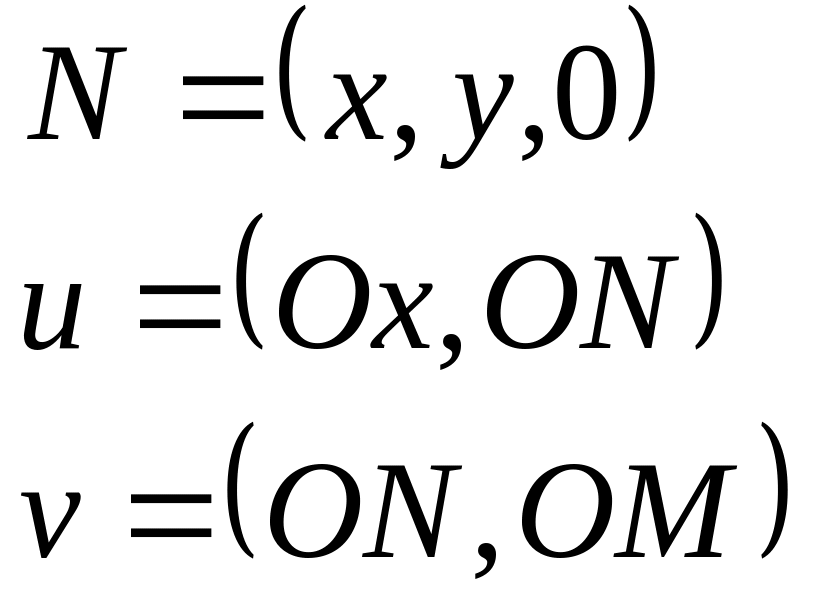
![]()
ОМ=r
![]()
![]()

u–линия получается,
если
![]() .
Точка М – описывает параллель,
u – линия параллели.
Найти v-линию, если
.
Точка М – описывает параллель,
u – линия параллели.
Найти v-линию, если
![]() .
v-линия есть меридиан.
Т.к. все v-линии –
меридианы. Все координатные линии на
сфере – параллели и меридианы.
.
v-линия есть меридиан.
Т.к. все v-линии –
меридианы. Все координатные линии на
сфере – параллели и меридианы.
Найдем угол φ,
![]() ,
для этого найдём угол φ между векторами
,
для этого найдём угол φ между векторами
![]() и
и
![]() ,
которые являются касательными
координатными линиями.
,
которые являются касательными
координатными линиями.
![]()
![]()
![]()
![]()
![]()
В любой точке сферы координатные линии ортогональны.
