2.Поняття моделі. Поняття інформаційної моделі. Поняття математичної моделі.

Модель — це штучно створений людиною абстрактний або матеріальний образ реального об’єкта,

що зберігає типові властивості оригіналу, важливі для розв’язання певної задачі.

Моделювання — процес створення, аналізу та уточнення моделі для подальшого дослідження

об’єкта моделювання.

Моделі створюють для того, щоб краще розуміти структуру, основні властивості, закони взаємодії

складових обєкта дослідження, навчитися керувати цим об’єктом та прогнозувати наслідки керування.

Розв’язання прикладної задачі вимагає створення моделі, яка описує реальні об’єкти та відносини між ними в межах даної задачі. Для досліджень об’єкта (явища, процесу) не обов’язково створювати матеріальну модель, часто досить надати необхідну інформацію про об’єкт у потрібній формі, тобто створити інформаційну модель.

Інформаційна модель — це абстрактний об’єкт, який замінює об’єкт оригінальний із метою його дослідження, зберігаючи при цьому типові риси та властивості оригіналу, важливі для дослідження. При створенні моделі треба визначити основні характеристики об’єкта та допустиму погрішність цих характеристик, вхідні характеристики, взаємовідносини характеристик.

Створення інформаційної моделі важливе, щоб зрозуміти структуру, основні властивості, закони взаємодії складових об’єкта, який аналізується, навчитися керувати цим об’єктом та прогнозувати наслідки реалізації керування.

Від поставленої задачі залежить повнота розробки та аналізу моделі.

Інформаційна модель може бути описана різними засобами: природною мовою, мовою математики, хімії, біології, мовою графічних структур тощо. 

Білет2

1.Лінійні простори, означення та властивості. Приклади лінійних просторів.

Означення 1. Нехай P – деяке числове поле, V – не порожня множина елементів довільної природи, і

а) в V введена операція додавання, причому множина V замкнена відносно неї;

б) означена операція множення числа 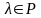на елемент 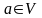, результат якої позначатимемо λа.

Множина V називається лінійним (векторним) простором над полем P, а її елементи векторами, якщо операції задовольняють аксіомам:

I. 1º. a+b=b+a (комутативність додавання),

2º. (a+b)+c=a+(b+c) (асоціативність додавання),

3º. 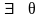, такий, що а+ θ=а, 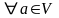. (θ називають нулем простору),

4º. 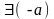такий, що а+(-а)=θ. Вектор (-а) називають протилежним для а.

II. 5º. 1a=a, де 1 – одиниця поля P,

6º. α(βа)=(αβ)а (асоціативність множення на число з поля P),

III. 7º. (α+β)а=αа+βа (дистрибутивність множення відносно додавання чисел з поля Р),

8º. α(а+b)=αa+αb (дистрибутивність множення відносно додавання в множині V).

Якщо Р – поле комплексних чисел, то простір називається комплексним лінійним простором.

Якщо Р – поле дійсних чисел, то простір називається дійсним лінійним простором.

Поле дійсних чисел позначатимемо надалі через R.

Приклади лінійних просторів

1. Множина всіх вільних векторів звичайного тривимірного простору – дійсний лінійний простір.

2. Простір T_n. Елемент х – вектор так званого арифметичного лінійного простору, - довільна впорядкована сукупність n дійсних чисел ξ₁, ξ₂, ..., ξ_n (n – фіксоване натуральне число):

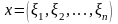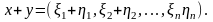Числа ξ_і називаються компонентами вектора х. Сумою векторів і називається вектор Добутком вектора х на дійсне число λ називається вектор

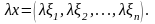
3. Простір С[a, b]. Елемент цього простору – довільна функція x=x(t) визначена і неперервна на [a, b].

4. Простір розв’язків однорідної системи лінійних рівнянь.

5. Простір многочленів. Множина всіх многочленів вигляду з комплексними коефіцієнтами 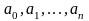при фіксованому n, очевидно, є комплексним лінійним простором відносно звичайних операцій додавання многочленів і множення многочлена на число. Цей простір називатимемо комплексним простором многочленів степеня не вище n.

6. Простір квадратних матриць. Додавання матриць і множення їх на числа виконуються за звичайними правилами означеними в розділі 5. Аксіоми 1º-8º виконуються.

7. Простір V, вектори якого додатні дійсні числа, основне поле – поле дійсних чисел.

Властивості лінійних просторів

1. В лінійному просторі існує єдиний нуль. 2. В лінійному просторі для кожного елемента існує єдиний протилежний елемент.3. Рівняння a+x=b (a,b V) розв’язне в V і має єдиний розв’язок.

4. αθ=θ.

5. 0а=θ, де 0 – нуль поля Р.