6.3. Определение скорости точки при естественном способе задания ее движения

Пусть движение точки А по заданной траектории происходит согласно уравнению , требуется определить скорость точки в момент времени t.

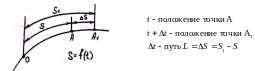
За промежуток времени точка прошла путь , значение средней скорости на этом пути

,

но оно отличается от значения скорости в момент времени t. Скорость в заданный момент t

,

т.е. значение скорости точки, движение которой задано естественным способом, в любой момент времени равно первой производной от расстояния (дуговой координаты) по времени.

Направление скорости, как отмечалось выше, известно заранее.

6.4. Определение ускорения точки при естественном способе задания ее движения

Вектор – ускорение точки в данный момент – есть геометри­ческая сумма касательного и нормального ускорений:

Вектор в любой момент времени направлен по касательной, поэтому вектор называется касательным, или тангенциальным ускорением. Модуль касательного ускорения

,

равный производной от скорости в данный момент по времени или, иначе, второй производной от расстояния по времени, характеризует быстроту изменения значения скорости.

Доказано, что вектор в любой момент времени перпендикулярен касательной, поэтому он называется нормальным ускорением.

Значит, модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент, обратно пропорционален радиусу кривизны траектории в данной точке и характеризует быстроту изменения направления скорости.

Модуль ускорения

,

а направление a (угол ) находим с помощью тригонометрических функций по одной из следующих формул:

.

Если векторы и направлены в одну и ту же сторону, то движение точки называется ускоренным. При этом зна­чения и имеют одинаковые знаки ( или ). Если же векторы и направлены в противоположные стороны, то движение точки называется замедленным. В этом случае знаки и разные ( или ).

6.5. Частные случаи движения точки

1. Прямолинейное движение. Если , то точка движется прямолинейно, так как при направление скорости остается неизменным.

2. Равномерное движение. При уравнение равномерного движения

.

При начальном расстоянии т.е. точка в момент начала движения находится в начале отсчета расстояний, уравнение равномерного движения упрощается: .

Если и , то движение точки называется равномерным прямолинейным. Если и , то точка движется равномерно по криволинейной траектории.

Равномерное движение точки по окружности

При таком движении и , так как при равномерном движении , а при движении по окружности . Из формулы скорость равномерного движения по окружности:

.

Если принять t = Т – периоду, т.е. времени одного обхода точкой окружности, то и

или ,

где - диаметр окружности.

3. Равнопеременное движение. Если , то движение точки называется равнопеременным.

Уравнение равнопеременного движения точки .

– скорость в любой момент времени.

и

а) При равнопеременном прямолинейном движении, если не знаем времени t, получим первую вспомогательную формулу

Если не знаем

,

где – средняя скорость точки при ее равномерном движении;

б) если равноускоренное движение точки начинается из начала отсчета траектории (S₀ = 0) и без начальной скорости ( ), то предыдущие формулы приобретают более, простой вид:

.

Примерами такого движения могут служить движение автомобиля при трогании с места или движение самолета на взлетной полосе, а также известное из физики свободное падение тел;

в) при свободном падении . В этом случае, если в формулах из пункта (б) заменить S высотой падения Н, они примут вид:

Предпоследняя из этих формул, представленная в виде , называется формулой Галилея.