Вправа 1. Задано граф матрицею суміжності r .

Необхідно:

1. задати граф геометричним способом;

2. задати граф аналітичним способом;

3. задати граф матрицею інцидентності;

4. визначити ступені вершин графів;

5. виділити три підграфи;

6. виділити маршрут довжиною 5;

7. виділити маршрут, який є ланцюгом;

8. виділити маршрут, який є шляхом;

9. виділити цикл у графі.

Варіанти матриці суміжності:

Вправа 2. Графи G₁ та G₂ задані матрицями інцидентності A₁ та A_2. Необхідно задати геометричним способом графи, отримані:

1. перетином заданих графів;

2. об’єднанням заданих графів;

3. кільцевою сумою заданих графів;

4. усуненням першої вершини графа G₁;

5. усуненням першого ребра графа G₂ ;

6. замиканням першої та другої вершини графа G₁ ;

7. стягуванням першого ребра графа G₂ .

Варіанти матриць інцидентності A₁ та A₂ :

Вправа 3. Граф заданий аналітичним способом. Необхідно:

1. задати граф геометричним способом;

2. встановити ступені вершин графу;

3. виділити три підграфи;

4. виділити маршрут довжиною 5;

5. виділити маршрут, який є ланцюгом;

6. виділити маршрут, який є шляхом;

7. виділити цикл.

Варіант 1. G₁ = < V₁, E₁, Θ₁ >

V₁ = {v₁, v₂, v₃, v₄, v₅};

E₁ = {e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₃};

Θ₁(e₁) = (v₁, v₁) , Θ₁(e₂) = (v₁, v₃) ,

Θ₁(e₃) = (v₁, v₃) , Θ₁(e₄) = (v₁, v₅) ,

Θ₁(e₅) = (v₂, v₃) , Θ₁(e₆) = (v₂, v₄) ,

Θ₁(e₇) = (v₂, v₄) , Θ₁(e₈) = (v₂, v₆) ,

Θ₁(e₉) = (v₃, v₃) , Θ₁(e₁₀) = (v₃, v₄) ,

Θ₁(e₁₁) = (v₄, v₅) , Θ₁(e₁₂) = (v₄, v₅) ,

Θ₁(e₁₃) = (v₅, v₅) .

Варіант 2. G₂ = < V₂, E₂, Θ₂ >

V₂ ={v₁, v₂, v₃, v₄, v₅};

E₂ = {e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₃};

Θ₂(e₁) = (v₁, v₂) , Θ₂(e₂) = (v₁, v₃) ,

Θ₂(e₃) = (v₁, v₄) , Θ₂(e₄) = (v₁, v₄) ,

Θ₂(e₅) = (v₁, v₅) , Θ₂(e₆) = (v₂, v₂) ,

Θ₂(e₇) = (v₂, v₃) , Θ₂(e₈) = (v₂, v₃) ,

Θ₂(e₉) = (v₂, v₅) , Θ₂(e₁₀) = (v₃, v₃) ,

Θ₂(e₁₁) = (v₃, v₄) , Θ₂(e₁₂) = (v₄, v₄) ,

Θ₂(e₁₃) = (v₄, v₅) .

Варіант3. G₃= < V₃, E₃, Θ₃ >

V₃ ={v₁, v₂, v₃, v₄, v₅};

E₃={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₃};

Θ₃(e₁) = (v₁, v₂) , Θ₃(e₂) = (v₁, v₂) ,

Θ₃(e₃) = (v₁, v₄) , Θ₃(e₄) = (v₁, v₄) ,

Θ₃(e₅) = (v₁, v₅) , Θ₃(e₆) = (v₂, v₂) ,

Θ₃(e₇) = (v₂, v₃) , Θ₃(e₈) = (v₂, v₅) ,

Θ₃(e₉) = (v₂, v₅) , Θ₃(e₁₀) = (v₃, v₄) ,

Θ₃(e₁₁) = (v₃, v₅) , Θ₃(e₁₂) = (v₄, v₄) ,

Θ₃(e₁₃) = (v₅, v₅) .

Варіант4. G₄= < V₄, E₄, Θ₄ >

V₄ ={v₁, v₂, v₃, v₄, v₅};

E₄={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂, e₁₃};

Θ₄(e₁) = (v₁, v₂) , Θ₄(e₂) = (v₁, v₂) ,

Θ₄(e₃) = (v₁, v₃) , Θ₄(e₄) = (v₂, v₂) ,

Θ₄(e₅) = (v₂, v₂) , Θ₄(e₆) = (v₂, v₄) ,

Θ₄(e₇) = (v₂, v₅) , Θ₄(e₈) = (v₃, v₄) ,

Θ₄(e₉) = (v₃, v₄) , Θ₄(e₁₀) = (v₃, v₅) ,

Θ₄(e₁₁) = (v₄, v₄) , Θ₄(e₁₂) = (v₄, v₅) ,

Θ₄(e₁₃) = (v₅, v₅) .

Варіант5. G₅= < V₅, E₅, Θ₅ >

V₅ ={v₁, v₂, v₃, v₄, v₅};

E₅={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂};

Θ₅(e₁) = (v₁, v₁) , Θ₅(e₂) = (v₁, v₃) ,

Θ₅(e₃) = (v₁, v₄) , Θ₅(e₄) = (v₁, v₅) ,

Θ₅(e₅) = (v₂, v₂) , Θ₅(e₆) = (v₂, v₄) ,

Θ₅(e₇) = (v₂, v₅) , Θ₅(e₈) = (v₃, v₃) ,

Θ₅(e₉) = (v₃, v₃) , Θ₅(e₁₀) = (v₃, v₅) ,

Θ₅(e₁₁) = (v₄, v₄) , Θ₅(e₁₂) = (v₄, v₅) ,

Варіант6. G₆= < V₆, E₆, Θ₆ >

V₆ ={v₁, v₂, v₃, v₄, v₅};

E₆={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁, e₁₂};

Θ₆(e₁) = (v₁, v₁) , Θ₆(e₂) = (v₁, v₄) ,

Θ₆(e₃) = (v₁, v₅) , Θ₆(e₄) = (v₂, v₂) ,

Θ₆(e₅) = (v₂, v₃) , Θ₆(e₆) = (v₂, v₄) ,

Θ₆(e₇) = (v₂, v₄) , Θ₆(e₈) = (v₃, v₃) ,

Θ₆(e₉) = (v₃, v₅) , Θ₆(e₁₀) = (v₃, v₅) ,

Θ₆(e₁₁) = (v₄, v₄) , Θ₆(e₁₂) = (v₅, v₅) ,

Вправа 4. Орграф G заданий аналітичним способом. Необхідно:

1. задати орграф геометричним способом;

2. встановити ступінь, напівступінь заходу та виходу кожної вершини графа;

3. виділити орієнтований маршрут, ланцюг, цикл та шлях у графі.

Варіант 1. G₁= < V₁, E₁, Θ₁ > V₁ ={v₁, v₂, v₃, v₄};

E₁={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀};

Θ₁(e₁) = (v₁, v₁), Θ₁(e₂) = (v₁, v₃) ,Θ₁(e₃) = (v₁, v₂), Θ₁(e₄) = (v₂, v₂),

Θ₁(e₅) = (v₂, v₄), Θ₁(e₆) = (v₃, v₂) ,Θ₁(e₇) = (v₃, v₃), Θ₁(e₈) = (v₃, v₄),

Θ₁(e₉) = (v₄, v₂), Θ₁(e₁₀) = (v₄, v₃) .

Варіант 2. G₂= < V₂, E₂, Θ₂ > V₂ ={v₁, v₂, v₃, v₄};

E₂={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉};

Θ₂(e₁) = (v₁, v₂), Θ₂(e₂) = (v₁, v₃), Θ₂(e₃) = (v₁, v₄), Θ₂(e₄) = (v₂, v₂),

Θ₂(e₅) = (v₂, v₃), Θ₂(e₆) = (v₃, v₁), Θ₂(e₇) = (v₃, v₃), Θ₂(e₈) = (v₄, v₁),

Θ₂(e₉) = (v₄, v₂) .

Варіант 3. G₃= < V₃, E₃, Θ₃ > V₃ ={v₁, v₂, v₃, v₄};

E₃={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉};

Θ₃(e₁) = (v₁, v₂), Θ₃(e₂) = (v₁, v₄), Θ₃(e₃) = (v₂, v₁), Θ₃(e₄) = (v₂, v₂),

Θ₃(e₅) = (v₃, v₂), Θ₃(e₆) = (v₃, v₃), Θ₃(e₇) = (v₄, v₁), Θ₃(e₈) = (v₄, v₂),

Θ₃(e₉) = (v₄, v₃) .

Варіант 4. G₄= < V₄, E₄, Θ₄ > V₄ ={v₁, v₂, v₃, v₄};

E₄={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉};

Θ₄(e₁) = (v₁, v₂),Θ₄(e₂) = (v₁, v₂), Θ₄(e₃) = (v₂, v₁), Θ₄(e₄) = (v₂, v₃) ,

Θ₄(e₅) = (v₂, v₄),Θ₄(e₆) = (v₁, v₂), Θ₄(e₇) = (v₃, v₃), Θ₄(e₈) = (v₄, v₁) ,

Θ₄(e₉) = (v₄, v₄) .

Варіант 5. G₅= < V₅, E₅, Θ₅ > V₅ ={v₁, v₂, v₃, v₄};

E₅={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀, e₁₁};

Θ₅(e₁) = (v₁, v₁),Θ₅(e₂) = (v₁, v₂), Θ₅(e₃) = (v₁, v₃), Θ₅(e₄) = (v₂, v₂),

Θ₅(e₅) = (v₂, v₃),Θ₅(e₆) = (v₂, v₄), Θ₅(e₇) = (v₃, v₁), Θ₅(e₈) = (v₃, v₃),

Θ₅(e₉) = (v₃, v₄),Θ₅(e₁₀) = (v₄, v₁), Θ₅(e₁₁) = (v₄, v₂).

Варіант 6. G₆= < V₆, E₆, Θ₆ > V₆ ={v₁, v₂, v₃, v₄};

E₆={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀};

Θ₆(e₁) = (v₁, v₁),Θ₆(e₂) = (v₁, v₃), Θ₆(e₃) = (v₁, v₄), Θ₆(e₄) = (v₂, v₁),

Θ₆(e₅) = (v₂, v₄),Θ₆(e₆) = (v₃, v₁), Θ₆(e₇) = (v₃, v₂), Θ₆(e₈) = (v₄, v₁),

Θ₆(e₉) = (v₄, v₂), Θ₆(e₁₀) = (v₄, v₄) .

Вправа 5. Як за матрицею інцидентності графа визначити, що в ньому є цикли довжиною 1, 2, 3, ...?

Вправа 6. Навести приклади графів: повного, дводольного і того, що має точки зчленування.

Вправа 7. Навести приклад програми на мові програмування та задати граф, який описує її структуру.

Вправа 8. Навести приклад простого графа та побудувати граф, який є доповненням до простого графа.

Вправа 9. Як за матрицею суміжності графа визначити, що в ньому в цикли довжиною 1, 2, 3, ...?

Вправа 10. Навести приклад графа, який містить більше ніж одну компоненту. Побудувати матрицю суміжності цього графа. Які особливості мають матриці суміжності графів, що мають більше як одну компоненту?

Вправа 11. Навести приклад к-часткового графу (к = 3, 4, 5). Побудувати матрицю суміжності цього графу. Які особливості мають матриці суміжності цього графу? Які особливості мають матриці суміжності к-часткових графів?

Вправа 12. Описати алгоритми здійснення операцій об’єднання та перетину графів, які задані матрицями інцидентності.

Вправа 13. Описати алгоритм здійснення операцій об’єднання та перетину графів, які задані матрицями суміжності.

Вправа 14. Які особливості мають матриці інцидентності та суміжності графів, що задані геометричним способом симетричними фігурами?

Вправа 15. Навести приклад повного дводольного графу. Побудувати матрицю інцидентності цього графу. Які особливості вона має?

Вправа 16. Навести приклад використання графів для зображення конкретних об’єктів дослідження в будь-якій науковій галузі, де операції над графами мали б сенс. Пояснити сенс операцій над графами в цій галузі.

Вправа 17. Нехай G_s - множина усіх підграфів графа G=( \/,E,θ ). Необхідно:

а/ перевірити замкненість операцій перетину та об’єднання на G_s ;

б/ якщо < G_s , ∩ , U > ~ алгебраїчна система, то визначити її тип та властивості операцій;

тип та властивості операцій.

Вправа 18. Яку мінімальну кількість ребер може мати граф G , який містить n вершин, щоб він залишався зв'язним?

Вправа 19. Навести приклад дерева, встановити співвідношення числа вершин та ребер, побудувати ряд піддерев.

Вправа 20. Побудувати кілька дерев графа, заданого у вправі 4.

Вправа 21. Геометрично задати два дерева, що містять n вершин кожна, причому в одному із них шлях максимальної довжини є мінімальним серед усіх дерев з n вершинами, а в другому - максимальним.

Вправа 22. Визначити кількість усіх шляхів будь-якої довжини між парою вершин повного графу з n вершинами.

Вправа 23. Користуючись інформацією про точки зчленування графа, як спростити визначення кількості шляхів між кожною парою його вершин?

Вправа 24. Визначити, чи є граф, який задано матрицею інцидентності А , ейлеревим, гамільтоновим. Які зміни необхідно зробити в графі, щоб він став ейлеревим, гамільтоновим?

Вправа 25. Задано матрицю суміжності R орграфа G . Необхідно:

І/ задати граф геометричним способом;

2/ задати граф аналітичним способом;

З/ задати граф матрицею інцидентності;

4/ визначити ступінь, півступінь заходу та півступінь виходу кожної вершини графа;

5/ визначити число всіх орієнтованих маршрутів довжиною 1,2,3 для кожної пари вершин;

6/ вилучити орієнтовані ланцюг, шлях та цикл у графі.

Варіанти матриці суміжності:

Приклад: Визначити число всіх орієнтованих маршрутів довжиною 1, 2, 3 для кожної пари вершин орграфу, заданого матрицею суміжності R₉ . Число орієнтованих маршрутів довжиною 1 між вершинами i, j задається елементом r_ij матриці R_{9 .} Число орієнтованих маршрутів довжиною 2 між вершинами i, j задається елементом r_ij² матриці R²₉ .

Тому необхідно побудувати матрицю R²₉ :

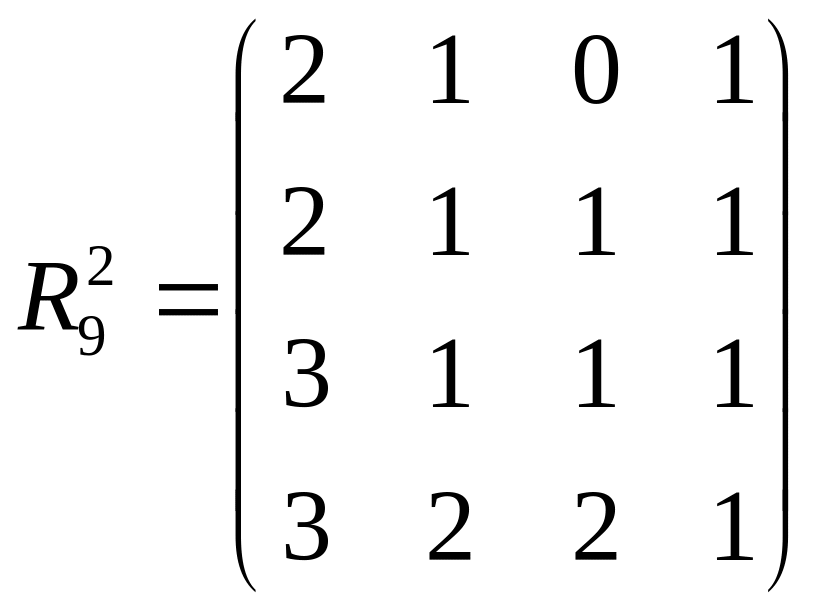
Наприклад, число орієнтованих маршрутів довжини 2 між вершинами З, 1 у даному випадку визначається елементом і дорівнює 3. Число орієнтованих маршрутів довжиною 3 між вершинами i, j задається елементом матриці R³₉ . Побудуємо матрицю R³₉ :

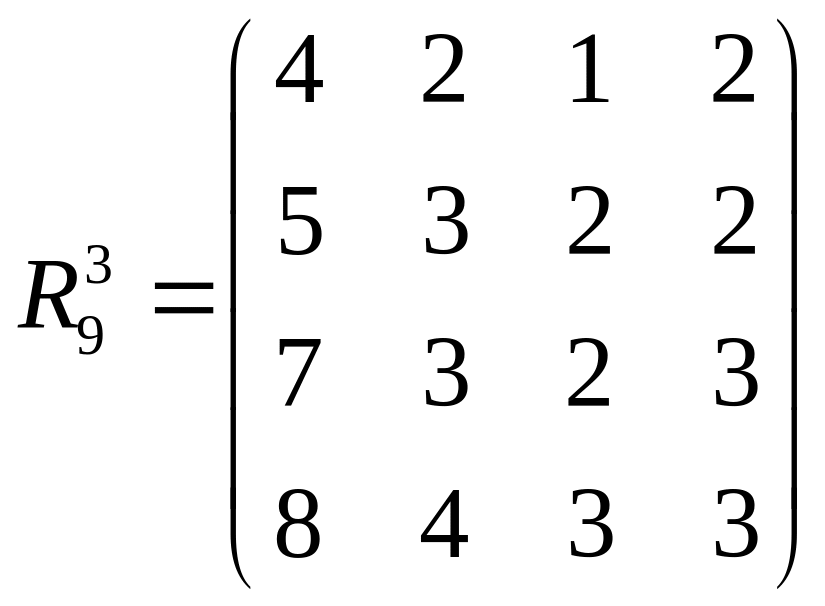
Наприклад, число орієнтованих маршрутів довжиною 3 між вершинами З, 1 в даному випадну визначається елементом і дорівнює 7 .

Вправа 26. Навести приклад кореневого дерева. Задати наведене дерево за допомогою дужкового запису.

Приклад: Задано кореневе дерево геометричним способом.

Лівий дужковий запис: v₀ ( v₁ (v₃, v₄) , v₂ (v₅, v₆ (v₈), v₇)) .

Правий дужковий запис: ((v₃, v₄ )v₁, ( v₅ (v₈) v₆, v₇) v₂) v₀ .

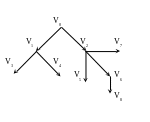
Зручно будувати, наприклад, лівий дужковий запис у такій послідовності: v₀ ( et(v₁) , et(v₂)) ,

де v₀ - коренева вершина, a et(v₁) та et(v₂)всі піддерева кореневі вершини яких зв’язані з коренем дерева одним ребром.

Далі et(v_i) подаємо за допомогою того ж самого засобу:

et(v_i) = v_i , якщо від вершини v_iі не виходить ні одного ребра. Таким чином , et(v₁) = v₁ (v₃, v₄ ), et(v₂) = v₂ (v₅,et(v₆), v₇) ; аналогічно одержуємо подання et(v₆) = v₆ (v₈).

Зараз легко підставити всі подання в один рядок:

v₀=(v₁ (v₃, v₄ ), v₂ (v₅,v₆ (v₈), v₇)).

Вправа 27. Задати геометричним способом кореневе дерево, лівий дужковий запис якого має вигляд:

1/ v₀ ( v_{1 ,}v₂ (v₃, v₄) , v₅ (v₆, v₇ (v₈))) ; 2/ v₀ ( v₁(v₂ (v₃, v₄) , v₅ (v₆, v₇ (v₈,v₉)))) ;

3/ v₀ ( v₁(v₂ (v₃(v₄,v₅ )))v₆) ; 4/ v₀ ( v₁,v₂,v₃,v₄, v₅ (v₆, v₇ (v₈))) ;

5/ v₀ ( v₁(v₂ (v₃(v₄(v₅ (v₆(v₇))))))) ; 6/ v₀ ( v₁(v₂ (v₃, v₄) , v₅ (v₆, v₇)),v₈) .

Вправа 28. Як за матрицею інцидентності орграфа визначити, чи є в ньому орієнтовані цикли довжиною 1, 2, 3, ...?

Вправа 29. Навести приклад орієнтованих ейлерева та гамільтонова графів.

Вправа 30. Як за матрицею інцидентності орграфа визначити його компоненти?

Вправа 31. Описати алгоритми виконання операцій перетину орграфів, які задані матрицею суміжності.

Вправа 32. Описати алгоритм виконання операцій перетину орграфів, які задані матрицею інцидентності.

Вправа 33. Визначити умови, яким має відповідати матриця суміжності орграфа, що є орієнтованим ейлеревим графом.

Вправа 34. Визначити умови, яким має відповідати матриця інцидентності орграфа, що є орієнтованим гамільтоновим графом.

Вправа 35. Теоретично обґрунтувати можливість або неможливість розв’язання такої розважальної математичної задачі: задано фігуру, чи можна намалювати цю фігуру, не віднімаючи пера від паперу більше двох разів і не перетинаючи більше одного разу жодну лінію?

Вправа З6. Довести або спростувати еквівалентність основному визначенню кореневого дерева такого визначення: "Кореневе дерево - орграф з коренем, в основу якого покладено граф, що є деревом”.

Вправа 37. Знайти максимальний потік крізь мережу N = (G, ), орграф G, якої задано геометричним способом.

Варіанти мережі:

1)

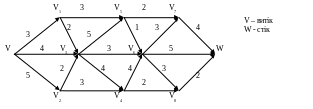
2)

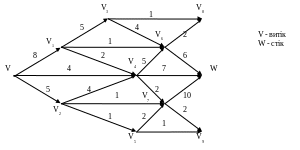
3)

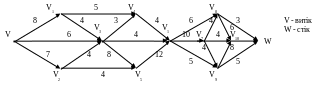
4)

5)

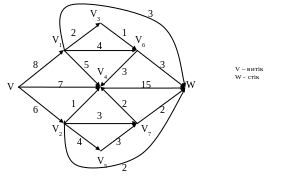
6)

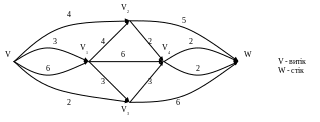
Вправа 38. Як треба модифікувати алгоритм знаходження максимального потоку, щоб використати специфічний вигляд орграфа мережі варіанта З вправи 37?

Вправа 39. Модифікувати алгоритм знаходження максимального потоку для мережі з більше, ніж одним стоком. Знайти за допомогою модифікованого алгоритму максимальний потік крізь: а/ мережу варіанту 2 вправи 37 з стоками v₈, v ₉,w б/ мережу варіанту 4 вправи 37 з стоками v₁, w.

Вправа 40. Нехай задано мережу

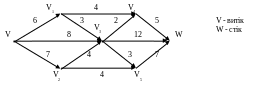
Показати, що наведений потік є максимальним для мережі

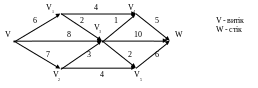
Вправа 41. Алгоритм знаходження максимального потоку для мережі з кількома стоками і витоками можна не модифікувати, якщо модифікувати саму мережу. В чому повинна полягати модифікація сітки?

Вправа 42. Чому при визначенні пропускної здатності розрізу в мережах не враховуються пропускні здатності ребер, початкові вершини яких належать підмножині, що містить стік, а кінцеві - підмножині, що містить витік?

Вправа 43. Описати алгоритм визначення максимального потоку, що виводиться безпосередньо із теореми Форда - Фалкерсона.

Вправа 44. Вказати перевагу відомих методів знаходження максимального потоку відносно методу повного перебору розрізів, що витікає із теореми Форда - Фалкерсона.