Тема 3.2. Прикладні та комбінаторні проблеми теорії графів.

[7; 19, гл.8. § 25-29, 21, гл.9, §30-33]

Вказівки щодо використання літературних джерел.

Багато проблем проектування комп’ютерів та електронних пристроїв, аналізу й синтезу систем управління мають комбінаторний характер. Оскільки вирішення таких проблем часто пов’язане із застосуванням графів, рекомендується ознайомитися з деякими результатами комбінаторного характеру в теорії графів.

Також рекомендується ознайомитися з "задачею про весілля", сформувати уявлення про паропоєднання й дослідити підхід до розв'язання задачі, запропонований Холлом. Цей результат широко застосовується для розв’язання різних проблем, зокрема побудови латинських квадратів, розфарбування ребер, складання розкладів.

Поняття трансверсалі (системи різних представників) зручне для постановки і розв’язання задачі вибору з т непустих підмножин R₁,..., R_m m різних елементів (по одному з кожної підмножини). Така формальна постановка може бути використана для ряду змістовних задач, наприклад для "задачі про весілля", складання розкладів та ін.

Для будь-якої множини підмножин визначення трансверсалі зручно починати з якоїсь простішої процедури перевірки умов її існування. Найважливіші результати теорії трансверсалей належать до встановлення цих умов.

Теорема Менгера - узагальнення теореми Холла. Слід звернути увагу на зв’язок теореми Менгера з відомим результатом Форда і Фалкерсона, про співвідношення потоків і розрізів у мережах.

Матроїд - формальне втілення ідеї незалежності. Рекомендується звернути увагу на зв’язок матроїдів і трансверсалей, ефективність їхнього застосування до розв’язання проблем теорії графів.

Методи й засоби теорії графів використовуються в теорії автоматів, граматик, прийняття рішень, для ілюстрацій алгебраїчних понять, а також для розв’язання багатьох практичних проблем. За даною темою вивчається матеріал, який вимагає об’єднання засобів і методів теорії графів та інших розділів математики.

Слід сформувати уявлення про проблеми планарності, укладання графів на площині, їхнє практичне значення й методи розв'язування.

Рекомендується ознайомитися з важливою у теоретичному і практичному плані проблемою розфарбування графів, зокрема планарних графів.

Спробуйте самі довести теорему про п’ять фарб або знайти слабке місце у доведені теореми у підручнику [19].

Слід ознайомитися з використанням знайомого нам поняття фактор-множини для аналогів відношень - орграфів без паралельних ребер.

Особливу увагу слід приділити ізоморфізму та ізоморфному вкладенню графів. Це зв’язано з тим, що графи широко використовуються при аналізі й синтезі систем управління, моделюванні структур, проектуванні ЕОМ та інших електронних пристроїв. Ізоморфізм графів або ізоморфне вкладення одного графа в інший таким чином означають можливість заміни однієї структури, системи, пристрою /або їхніх частин/ на іншу структуру, систему, пристрій /або їх частину /.

Дуже важливо тому для заданих графів уміти встановлювати їх ізоморфізм або ізоморфне вкладення. Виявилось, що задача ця дуже трудомістка. Розв'язується вона шляхом створення алгоритмів встановлення ізоморфізму та ізоморфного вкладення графів для графів різних видів з урахуванням специфічних особливостей графів кожного виду.

Цей підхід дозволяє створити алгоритми з допустимою оцінкою трудомісткості.

Після вивчення відомих алгоритмів рекомендується спробувати створити нові алгоритми для окремих видів графів.

Вправи до теми 3.2.

Вправа 1. Задати відношення вправи 8 теми 1.1 за допомогою графа. Які особливості має граф, що відповідає рефлексивному, симетричному, транзитивному відношенням, відношенню еквівалентності.

Приклад: Відношенню α₁ відповідає орграф G₁. Аналітично G₁ можна подати у такому вигляді:

G ₁= < V₁, E₁, Θ₁ >,

V ₁={1,2,3,4,5,6}, E₁={e₁,e₂,e₃},

Θ₁(e₁)=(1,2), Θ₁(e₂)=(4,3), Θ₁(e₃)=(6,6).

Відношенню α₂ відповідає орграф G₂. Аналітично G₂ можна подати у такому вигляді: G₂= < V₂, E₂, Θ₂>,

V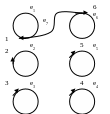 ₂={1,2,3,4,5,6},

E₂={e₁, e₂, e₃, e₄, e₅, e₆, e₇},

Θ₂(e₁)=(1,1), Θ₂(e₂)=(2,2),

Θ₂(e₃)=(3,3), Θ₂(e₄)=(4,4),

Θ₂(e₅)=(5,5), Θ₂(e₆)=(6,6),

Θ₂(e₇)=(1,6).

Відношенню α₃ відповідає орграф G₃ . Аналітично G₃ можна подати у такому вигляді: G₃= < V₃, E₃, Θ₃ >,

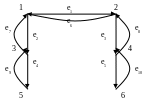V₃={1,2,3,4,5,6}, E₃={e₁, e₂, e₃, e₄, e₅, e₆, e₇, e₈, e₉, e₁₀},

Θ₃(e₁)=(1,2), Θ₃(e₂)=(1,3), Θ₃(e₃)=(2,4),

Θ₃(e₄)=(3,5), Θ₃(e₅)=(4,6), Θ₃(e₆)=(2,1),

Θ₃(e₇)=(3,1), Θ₃(e₈)=(4,2), Θ₃(e₉)=(5,3),

Θ₃(e₁₀)=(6,4).

Відношенню α₃ відповідає орграф G₄. Аналітично G₄ можна подати у такому вигляді: G₄ = < V₄, E₄, Θ₄>,

V₄={1,2,3,4,5,6}, E₄={e₁, e₂, e₃, e₄, e₅, e₆, e₇},

Θ₄(e₁)=(1,2), Θ₄(e₂)=(2,3), Θ₄(e₃)=(1,3),

Θ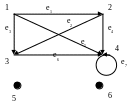 ₄(e₄)=(2,4), Θ₄(e₅)=(1,4), Θ₄(e₆)=(3,4),

Θ₄(e₇)=(4,4).

Легко помітити, що аналітичне завдання орграфа і графік відповідного відношення мають такий же самий набір пар.

Вправа 2. Навести приклад орграфа, який відповідає відношенню часткового порядку на множині, яка не є лінійно впорядкованою.

Вправа 3. Навести приклад орграфа, який відповідає відношенню часткового порядку на лінійно впорядкованій множині.

Вправа 4. Визначити розрізувальну множину зв’язного графу, заданого матрицею інцидентності А .• Визначити розрізи графа.

В аріанти матриці інцидентності:

Вправа 5. Визначити розрізувальні множини та розрізи в графах, які задані геометричним способом.

Варіанти графів

1)

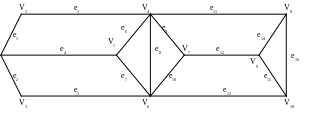
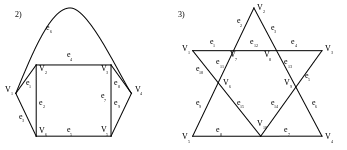
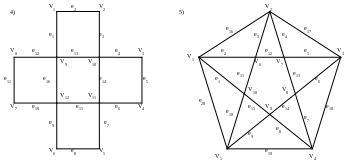
Вправа 6. Скільки розрізувальних множин має повний двочастковий граф з n вершинами?

Вправа 7. Навести приклад зв’язного графу, що має розрізувальну множину, яка містить одне ребро.

Вправа 8. Навести приклад зв’язного графа з n вершинами, один розріз якого породжує максимальну кількість компонентів.

Вправа 9. Вказати для кожної із наступних підмножин ребер графу, заданого в п. З вправи 5, чи є вона розрізом, чи розрізу­вальною множиною:

1) { e₁ , e₁₀ }; 2) { e₂ , e₆ , e₁₂ , e₁₄ };

3) { e₁ , e₈ , e₁₄ , e₁₅ }; 4) { e₂ , e₃ , e₁₂ };

5) { e₃ , e₁₀ }; 6) { e₂ , e₃ , e₄ , e₅ };

7) { e₃ , e₆ }; 8) { e₂ , e₄ , e₅ , e₁₂ };

9) { e₂ , e₃ , e₆ , e₁₂ , e₁₄ }.

Приклад: Розглянемо підмножину {e₄, e₅}. Вона є розрізом, оскільки e₄ та e₅ - єдині два ребра, що зв’язують вершини із підмножин

V₁= {U₃} і V₂= {U₁, U₂, U₄, U₅, U₆, U₇, U₈, U₉, U₁₀ },

а V₁ і V₂ є розбиття. Крім того, { e₄ , e₅ }.- розрізувальна множина, оскільки на V₁ та V₂ визначені зв’язні компоненти.

Розглянемо підмножину { e₄ , e₅ , e₆ , e₇ }. Вона є розрізом. Оскільки її і тільки її ребра зв’язують вершини із підмножин

V₁= {U₃ , U₄} та V₂= {U₁, U₂, U₅, U₆, U₇, U₈, U₉, U₁₀ },

а V₁ та V₂. є розбиття множини V. Але підмножина { e₄ , e₅ , e₆ , e₇ } не є розрізувальною множиною, оскільки { e₄ , e₅ }. { e₄ , e₅ , e₆ , e₇ }-розрізувальна множина.

Розглянемо підмножину { e₄ , e₅ , e₁₃ }. . Вона не є розрізувальною множиною, оскільки цю властивість має її підмножина { e₄ , e₅ }. Крім того, вона не є розрізом, оскільки не можна вилучити розбиття таке, що ребра із { e₄ , e₅ , e₁₃ } зв’язують тільки вершини із різних під множин розбиття.

Вправа 10. Вказати для кожної із поданих підмножин ребер графу, заданого в п. 2 вправи 5, чи є вона розрізом, чи розрізувальною множиною:

1) { e₁ , e₃ , e₄ , e₅ , e₆ }; 2) { e₁ , e₂ , e₆ };

3) { e₈ , e₉ }; 4) { e₄ , e₅ , e₆ };

5) { e₁ , e₂ , e₈ , e₉ }; 6) { e₂ , e₄ , e₅ , e₆ };

7) { e₂ , e₃ , e₇ , e₉ }; 8) { e₁ , e₃ , e₄ , e₅ }.

Вправа 11. Задати геометричним способом граф, ребра якого інцидентні будь-якій вершині, не утворюють розрізувальну множину. Чи існує розв’язання для скінчених графів?

Вправа 12. Задати граф, ребра якого інцидентні будь-якій вершині, утворюють розрізувальну множину.

Вправа 13. Встановити планарність графів вправи 5.

Вправа 14. Навести приклади непланарних графів і довести їх непланарність.

Вправа 15. Навести графи, двоїсті графам вправи 5.

Вправа 16. Встановити планарність графів вправи 5, використовуючи двоїсті їм графи.

Вправа 17. Встановити хроматичне число графів вправи 5.

Вправа 18. Встановити хроматичне число цикла з п вершинами.

Вправа 19. Встановити хроматичне число повного графа з п вершинами.

Вправа 20. Вказати особливості розфарбування двочасткових графів. Залежить чи ні хроматичне число дводольного графа від того є він повним чи ні?

Вправа 21. Описати алгоритм побудови двоїстого графа за матрицею суміжності графа.

Вправа 22. Описати алгоритм побудови двоїстого графа за матрицею інцидентності графа.

Вправа 23. Вказати особливості розфарбування зв’язних ациклічних графів.

Вправа 24. Встановити планарність та розфарбувати графи вправи 1 теми 3.1.

Вправа 25. Вказати особливості графа, двоїстого зв’язному ациклічному графу.

Вправа 26. Навести приклади карт, розфарбування яких може призвести до необхідності розфарбування графів вправи 1 теми 3.1.