Тема 1.1. Загальний аналіз засобів моделювання дискрет­ної математики.

[13, вступ, гл.1; 10, вступ, частина І, гл.1 - 4; 1, гл.0, розд.1. § 1-3. 5, 6; 2, гл.1, § 1, 3-5; гл.2, § І, 2, 4, 5, 8, 9, 10; гл.3. § 1-3; 3, гл.1, § 1- 4; 2, гл.2, § 5. гл.9, § 8. гл.10, § 7; 3. гл.1. §3; 2, гл.9. § І, 2. 5, 7; 3, гл.1, § 4; 8, гл.1]

Вказівки щодо використання літературних джерел.

Для інженера з комп’ютеризованих систем управління і автоматики дискретна математика є сильним інструмен­том аналізу й проектування, тому вивчення мате­матичних засобів і методів корисно пов’язати з класами проблем, що ним розв’язуються.

Рекомендується почати вивчення курсу а формування уявлення про систему, управління, систему управління і кібернетичний під­хід до управління з використанням комп’ютерної техніки. Необхідно зрозуміти схему управління із зворотним зв’язком і роль процесів оброблення інфор­мації у реалізації цієї схеми.

ОУ – об’єкт управління

СУ – система управління

У концентрованій формі нову категорію “управління” та її зв’язок з інформацією визначив Норберт Вінер: “Сутність принципу управління в тому, що рух і дія великих мас або передача й пере­творення великих кількостей енергії спрямовуються і контролюють­ся за допомогою невеликих кількостей енергії, що несуть інформа­цію" [13].

Кібернетичний підхід до управління передбачає аналіз об’єкта управління. Цей аналіз завершується побудовою моделі функціону­вання об’єкта, формулюванням задачі управління і алгоритму її розв’язання, зображенням алгоритму розв’язання мовою програмуван­ня для комп’ютера.

Дискретна математика забезпечує системотехніка засобами й методами реалізації кожного з етапів кібернетичного підходу.

Найважливіші питання теми - мікропідхід до дослідження систем управління шляхом моделювання й роль математики як джерела засобів і методів моделювання, алгоритмізації, програмування для реаліза­ції підходу, а також проблема штучного інтелекту й реакція мате­матики на його вимоги до математичних засобів і методів.

При розгляді матеріалу треба пам’ятати, що головне завдання курсу - сформувати математичний фундамент освіти інженера з комп’ютеризованих систем управління і автоматики, а також прищепити вміння цілеспрямовано добудовувати його знаннями, одержаними при вивченні інших курсів. Важливим елементом цієї освіти є загальне уявлення про засоби моделювання дискрет­ної математики.

Тому далі у матеріалі цієї теми впроваджуються основні поняття - множини, операції на множинами, функції, відношення, окремих класів відношень, насамперед порядку і еквівалентності, базові поняття комбінаторики тощо.

Зверніть увагу на те, що поняття множини по суті початкове поняття математики й звичного визначення, побудованого із за­гальніших понять, не має. Але всі наступні поняття вводяться з визначенням, у яких використовуються поняття множини та інші загальні поняття. Важливо зрозуміти, щодо елементів множини спочатку важливо лише те, що ми їх повинні виділяти як окремі об’єкти. Але коли ми переходимо до способів описання множини і її елементів, то відсутність обмежень може привести до парадоксів.

Групування елементів із однієї сукупності легко дозволить ввести і зрозуміти поняття підмножини, відношення включення і рівності множин. Властивості операцій над множинами виразніше проявляються на геометричних зображеннях, що називаються діаграмами Венна або колами Ейлера:

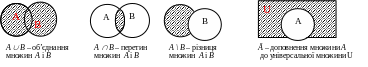
Без поняття універсальна множина не можна визначити операцію доповнення множин. На прикладі всіх підмножин універсальної множини ми вводимо об’єкт, що пов’язує матеріал із різних розділів дискретної математики - булеан множини. Якщо введемо поняття впорядкованих пар і прямого (декартового) добутку множини A на множину B як мно­жину, елементами якої є всі можливі пари (x,y), x  A, у  B, дістанемо можливість визначити функції від одного аргументу і бінарного відношення як підмножини декартового добутку. Перехід до впорядкованих трійок, четвірок, n-ок дозволить визначити прямий (декартів) добуток n множин і відповідно функції від n аргументів і n-місні відношення.

Зазначте, що в науковій літературі часто поняття функції ототожнюється з поняттям відображення. Рекомендується розглянути різноманітну термінологію, пов’язану з визначенням функцій, насамперед, образ і прообраз, аргумент і значення, область і кообласть функції. Для опрацювання технічної літератури і розв’язання практичних проблем важливо познайомитися з класами функцій: ін’єктивних, сюр’єктивних, бієктивних, всюди визначених і часткових функцій, функціями із множини S в множину S.

Продемонструємо можливі помилки, що супроводжують опрацювання поняття функції. Формально, функція із множини A у множину B - це така підмножина F декартового добутку A  B, що для кожного x A в ній міститься не більше однієї пари (x,y), де у B. Одна з типових помилок при визначенні функції – підміна визначення поняття його позначенням. Наприклад, помилково функцію із множини A у множину B визначають як “таку підмножину F декартового добутку A  B, що для кожного x A виконується умова у = F(x)”. Пояснимо цю помилку. Визначивши функцію із множини A у множину B як таку підмножину F декартового добутку A  B, що для кожного x A в ній міститься не більше однієї пари (x,y), де у B, ми вводимо відповідне позначення для цього факту і домовляємося записувати у = F (x), якщо (x,y)  F. В наведеному помилковому визначенні введене позначення факту сприймається як визначення об’єкту.

Узагальнення наведеного матеріалу важливо доповнити уявленнями про функціональний підхід в математиці і його значення, розглянути принцип двоїстості, тотожні перетворення виразів, ввести в коло об’єктів дискретної математики відомі із інших дисциплін поняття вектора, компоненти вектора тощо.

Попрацювавши з функціями, поверніться до бінарних відношень, повторіть їхні визначення і переходьте до аналізу їхніх властивостей. На численних прикладах, наведених у електронному конспекті та прикладах до вправ розгляньте способи задання відношень, важливі поняття композиції відно­шень, оберненого відношення і класи відношень: рефлексивні (антирефлексивні, іррефлексивні), симетричні (асиметричні, антисиметричні), транзитивні (не транзитивні). Потім можна розглядати відношення еквівалентності і різноманітні відношення порядку як відношення з певними наборами властивостей. При цьому відношення еквівалентності порівняйте з розбиттям, сформуйте уявлення про класи еквівалентності. В процесі аналізу відношень порядку пов’язуйте уявлення про ієрархію, впорядкованість і відношення, строгий та частковий порядок, а потім переходьте до понять частково і повністю впорядкованих множин та фундаментальних понять впорядкованих множин (найбільших і найменших, мінімальних та максимальних елементів, верхніх і нижніх меж і граней тощо.

Природнім і найбільш поширеним способом формування нових об’єктів дискретної математики є процес ускладнення відомих математичних об’єктів. Слідуючи цим шляхом, розширте свої уявлення про функції (функціями слідування Пеано, операціями над функціями - композицією, підстановкою, оберненими і оборотними функціями, теоремами про існування обернених і оборотних функцій, спеціальними класами функцій: підстановками, циклами, з’єднанням, послідовностями, функціоналами) і відношення (транзитивними та рефлексивними замиканнями відношень) тощо.

Формування уявлення про об’єкти, що вводяться, варто супро­воджувати розглядом реальних проблем аналізу й синтезу систем управління, при розв’язуванні яких корисно використовувати вве­дені об’єкти. Так, множини застосовуються для описання систем, операції, функ­ції, відношення - для описання зв’язків між елементами систем.

Ідеальним прикладом використання теоретичних понять до розв’язання практичних проблем є застосування відношень для подання структури даних, що зберігаються в базах даних, і формалізації операцій над файлами у вигляді теоретико-множинних операцій. В цьому плані рекомендується розглянути достатню для повного розуміння кількість прикладів зображення відношеннями структур даних, необхідну термінологію (файли, записи, поля, бази, таблиці, атрибути, домени, ключі), пересвідчитися на прикладах у необхідності нормальних форм, насамперед першої, другої, третьої, і перейти до функціональної залежності атрибутів і нормалізації відношень.

Другим джерелом уявлень про нові математичні об’єкти є застосування різних принципів формалізації тих же інтуїтивних понять. Так, відношення можна розглядати як графи. Наявність геометричного способу задання орграфів вплинула на уявлення про бінарні відношення та аналіз їх властивостей. Останні наочно зображують графами, які роблять очевидними власти­вості відношень. Наприклад, рефлексивність відношення пов’язана з петлями у відповідному графі, транзитивність - з наявністю ребра (v_i, v_j), якщо є шлях (v_i, v_k), (v_k, v_j). Це ребро називається транзитивно замикаючим.

При зображенні частково-упорядкованих множин орграфами часто опускають петлі й транзитивно замикаючі ребра. Такі орграфи нази­вають діаграмами Хассе.

Третім джерелом виникнення нових математичних об’єктів є подання у такому вигляді часткових випадків відомих математичних об’єктів. Тому важливо розширити свої уявлення про часткові випадки вже відомих понять, введення яких дозволяє розв’язувати нові проблеми в управлінні. Саме до таких належать поняття решітки. Треба, грунтуючись на уявленнях про межі й грані, вивчити решітки як частково упорядковані множини, в яких кожні два елементи мають верхню й нижню грані, розглянути достатню кількість прикладів решіток.

Решітки можна задавати з допомогою згаданих вище діаграм Хассе, що дає можливість глибше зрозуміти особливості решіток. Згідно з теорією прийняття рішень - ця схема дуже зручна для вибору рішень. Дійсно, управління завжди містить елемент вибору. Поняття порядку, і в тому числі часткового порядку, вводить основу для фіксації переваги одних рішень перед іншими. Якщо на множині альтернативних рішень задано відношення порядку, можна спробувати знайти найкраще рішення.

У тому разі, коли множина лінійно упорядкована, це легко зробити. Але не завжди множина альтернатив лінійно упорядкована. Якщо існують альтернативи, між якими встановлено відносини байдужості, тоді вибір найкращого рішення можливий при наявності тільки одного мінімального (максимального) елемента при розв'язанні задачі на мінімум (максимум).

Решітка має єдиний мінімальний і максимальний елемент. Тому вона зручна. Крім того, найчастіше деякі з альтернативних рішень неможливо реалізувати при наявних ресурсах, найчастіше - найкращі рішення. Це враховується шляхом обмежень на множині альтернативних рішень. Тому наявність у решітці граней для кожної пари елементів дозволяє порівняти кожну пару рішень. Тим самим зберігається цінність решітки для прийняття рішень при деяких вилученнях елементів із множини альтернатив.

Все це визначає велику цінність глибокого вивчення решіток для спеціаліста з управління. Вивчення решіток вилилось у значну галузь дискретної математики - теорію решіток, основи якої викладені у [8] .

Важливе місце для дослідження різних математичних об’єктів мають поняття факторизації та ідеалу. Слід ознайомитися з поняттям фактор-множини і його використанням для заданння відношень, засвоїти факторизацію функцій.

Вправи до теми 1.1.

Вправа 1. Нехай маємо універсальну множину U = {a,d,c,d,e,f,g,h}. Необхідно задати об’єднання, перетин, різницю множин S та T, доповнення множини S до множини U, доповнення множини S  T до множини U.

Варіанти задання множин S та T:

1. S = {a,b,c}; T = {b,c,f}; 6) S = {g,d,f,a}; T = {b,c,e};

2. S = {d,f,g}; T = {d,g,h}; 7) S = {a}; T = {a,b,f,h};

3. S = {a,b,c,d};T = {d,e,f,g}; 8) S = {a,b,e,f}; T = ;

4. S = {h,g,d}; T = {a,b,d,g}; 9) S = U; T = {a,b,e,h};

5. S = {g,d,b,c};T = {b,c,d}; 10) S = U; T = .

Приклад: S = {a,b,c}, T = {b,c,f}. Об’єднання S  T = {a,b,c,f}. Перетин S  T = {b,c}. Різниця S\T = {a}. Декартів добуток S  T = {(a,b), (a,c), (a,f), (b,b), (b,c), (b,f), ), (c,b), (c,c), (c,f)}. Доповнення S = {d,e,f,g,h}. Доповнення (ST) = {a,d,e,f,g,h}.

Вправа 2. Навести множину всіх підмножин множини S із вправи 1.

Приклад: S = {a,b,c}. Тоді множина всіх її підмножин

P(S) = {Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}.

Вправа 3. Нехай S та T - множини із вправи 1. Необхідно задати:

1. Функцію із множини S в множину T: а) довільну; б) ін’єктивну; с) сюр’єктивну; г) бієктивну.

Приклад: F₁ = {(a,b), (b,b), (c,c)} – довільна функція із множини S в множину T;

F₂ = {(a,b), (b,c), (c,f)} - сюр’єктивна функція із множини S в множину T;

F₂ також є ін’єктивною, отже, вона є бієктивною функцією із множини S в множину T.

2. Довільну функцію із множини T в множину S.

Приклад: F₃={(b,c), (c,b), (f,a)} - довільна функція із множини T в множину S.

3. Ліву та праву композиції функції із множини T в множину S та функції із множини S в множину T.

Приклад: F₁ ◦ F₃ = {(b,c), (c,b), (f,b)} - ліва композиція;

F₁ ◊ F₃ ={(c,b), (b,c), (a,c)} - права композиція.

4. Функцію із множини S в множину S.

F₄ = {(a,b), (b,с), (c,а)} - довільна функція із множини S в множину S.

5. Тотожні функції 1_S та 1_T.

Приклад: S = {a,b,c}; T = {b,c,f}.

1_S = {(a,a), (b,b), (c,c)}, 1_T = {(b,b), (c,c), (f,f))}.

6. Обернену зправа та зліва для бієктивної функції із множини S в множину T.

Приклад: F₂ - бієктивна функція із множини S в множину T;

F = {(b,a), (c,b), (f,c)} – обернена зліва для функції F₂ , знайдена з рівняння F ◦F₂ = 1_S чи F ◦ {(a,b), (b,c), (c,f)} = {(a,a), (b,b), (c,c)};

F = {(b,a), (c,b), (f,c)} - обернена зправа для функції F₂ , знайдена з рівняння F₂ ◦ F = 1_T чи {(a,b), (b,c), (c,f)} ◦ F = {(b,b), (c,c), (f,f)}.

7. Обернену зправа та зліва для ін’єктивної, але не сюр’єктивної функції із множини S в множину T.

Приклад: Нехай S = {a,b}, T = {b,c,f}. Функція F₅= {(a,b), (b,c)} - ін’єктивна, але не сюр’єктивна функція із множини S в множину T.

F’₅ = {(b,a,), (c,b)} – часткова функція із множини T в множину S, обернена зліва для функції F₅ , знайдена з рівняння F’₅ ◦ F₅ = 1_S чи F’₅ ◦{(a,b), (b,c)} = {(a,a), (b,b)}.

Функції із множини T в множину S, оберненої зправа для функції F₅, не існує, оскільки рівняння

F₅ ◦ F’₅ = 1_T чи {(a,b), (b,c)} ◦ F”₅ = {(b,b), (c,c), (f,f))} не має розв’язку на множині функцій із множини T в множину S.

8. Обернену зправа та зліва для сюр’єктивної, але не ін’єктивної функції із множини S в множину T.

Приклад: Нехай S = {a,b,c}, T = {c,f}. Функція F₆= {(a,c), (b,c), (c,f)} - сюр’єктивна, але не ін’єктивна функція із множини S в множину T. Функція F”₆ = {(c,a,), (f,c)} - обернена зправа для F_{6 ,} знайдена з рівняння

F₆ ◦ F”₆ = 1_T чи {(a,c), (b,c), (c,f) } ◦ F”₆ = {(c,c), (f,f)}.

Оскільки рівняння має ще один ров’язок F”₆ = {(c,b,), (f,c)}, то цей ров’язок теж становить функцію, обернену справа для функції F_{6 .}

Функції із множини Т в множину S, оберненої зліва для функції F₆, не існує, тому що рівняння

F ^’₆ ◦ F = 1_s чи F’₆ ◦ {(а,с),(b,c),(с,f)} = {(а,а),(b,b),(с,с)} не має розв’язку на множині функцій із множини Т в множину S (хоч це рівняння має розв’язок на множині бінарних відношень):

F’₆ = {(с,a),(с,b),(f,c)}.

Вправа 4. Чи для всіх пар множин S та Т із вправи 1 можливо задати бієктивну функцію із множини S в множину T?

Вправа 5. Чи існують обернена зліва та зправа функції для функції, яка не є ні ін’єктивною, ні бієктивною?

Вправа 6. На довільних множинах задати функції такі, щоб серед них була сюр’єктивна, ін’єктивна, бієктивна.

Вправа 7. Нехай Z - множина цілих чисел, z  Z . Встановити властивості функцій, які задані такими відображеннями:

a) z  z ² ; б) z  - z ; в) z  2 z ; г) z  z+1 ; д) z  |z| .

Вправа 8. Необхідно задати чи установити відсутність обернених зліва та зправа функцій для таких функцій, які задані на множині цілих чисел (х,у  Z):

1) y = x²; 2) y = x; 3) y = x³; 4) y = 2x;

5) y = x +1; 6) y = x² + x; 7) y = x⁴; 8) y = |x|.

Приклад: нехай задана функція y = f₀(x)= 2х. Ця функція f₀: Z Z ін’єктивна, скрізь визначена, але не сюр’єктивна (наприклад, число1 не може бути значенням функції для жодного значення аргументу).

Ліву обернену функцію x= f₁(y); f₁: Z  Z для функції f₀ знаходимо з рівняння f₁ ◦ f₀ = 1_Z (можна використовувати операцію правої композиції, записуючи рівняння у вигляді f₀ ◊ f₁=1_Z). Аналізуємо рівняння. Кожному цілому числу функція f₀ ставить у відповідність парне число. Права частина рівняння вимагає відобразити це парне число в вихідне ціле число. Очевидно, це може забезпечити функція x= f₁(y) = ¹/₂ y. Дійсно, підставляючи функцію f₁(y) у рівняння, впевнимося у тому, що воно обертається на тотожність.

Праву обернену функцію x= f₂(y) знаходимо, розв’язуючи рівняння f₀ ◦ f₂ = 1_Z (можна використовувати рівняння f₂ ◊ f₀ = 1_Z). Природно, що функція x= ¹/₂ y претендує й на місце правої оберненої функції. Але рівняння для оберненої cправа функції, у такому разі, в тотожність не обертається. Так, ми не здатні відобразити саме у себе будь-яке непарне число, тому що функція x= ¹/₂ y не визначена на непарних числах.

Таким чином, підтверджується відомий факт, що не сюр’єктивна функція оберненої cправа не має. Якби функція y= f₀(x) була задана у вигляді f₀ : Z  P, де Р - множина усіх парних чисел, то рівняння f₀ ◦ f₂ = 1_P мало б розв’язок. Але у цьому випадку функція f₀ є сюр’єктивною, залишаючись скрізь визначеною та ін’єктивною, отже, вона є бієктивною функцією. До того ж, функція f₁ залишається оберненою зліва функцією для заданої таким чином функції f₀. Підтверджується ще один відомий факт - бієктивна функція має ліву та праву обернені функції.

Вправа 9. Нехай S та T - множини із вправи 1. Необхідно задати довільне бінарне відношення між множинами S та Т за допомогою: а) графіка; б) матриці.

Приклад: Нехай S = {а,b,с}; Т = {b,c,f}. Тоді кожна підмножина декартового добутку S  T, який наведено у прикладі до вправи 1, є відношенням, заданим за допомогою графіка, наприклад:

α = {(a,b), (а,c), (a,f), (c,c)}. Відношення α можна задати матрицею

R= ||r_ij|| , де r_ij =1 , якщо (S_i, Т_j)  α та r_ij = 0, якщо (S_i, Т_j)  α.

Для відношення α матриця R має такий вигляд:

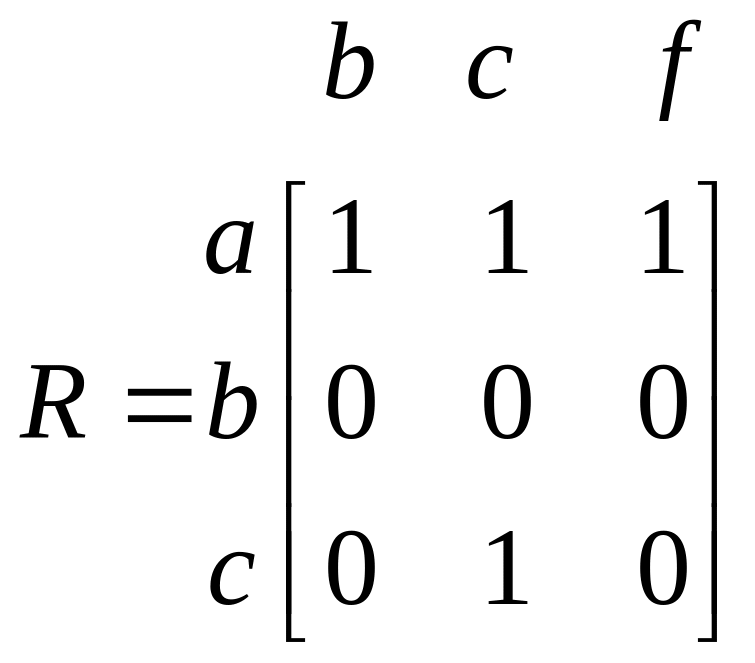
Вправа 10. Нехай задана множина Х. Необхідно задати за допомогою графіка відношення на Х: а) довільне; б) рефлексивне; в) симетричне; г) антисиметричне; д) транзитивне; е) таке, що мало б змістовну інтерпретацію.

Варіанти задання множини Х:

1) X = {1,2,3,4,5,6}; 2) X = {a,b,c,d,f};

3) X = {5,6,7,8,9,10}; 4) X = {000, 001, 010, 011, 100, 101, 110, 111}.

Приклад: α = {(1,2), (4,3), (6,6)} - довільне відношення;

α₂ = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,6)} - рефлексивне відношення;

α₃ = {(1,2), (1,3), (2,4), (3,5), (4,6), (2,1), (3,1), (4,2), (5,3), (6,4)} - симетричне відношення;

α₄ = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5),.(4,6), (5,6)} - антисиметричне відношення;

α₅ = {(1,2), (2,3), (1,3), (3,4), (1,4), (2,4), (4,4)} - транзитивне відношення.

Варто зауважити, що відношення α₄ є також рефлексивним та транзитивним;

α₆ = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,2), (2,4), (2,6), (3,3), (3,6), (4,4), (5,5), (6,6)}-це відношення можна задати, як відношення "x₁ ділить x₂ націло", де (x₁, x₂) - кожна пара з графіка відношення.

На множині Х = {0,1,2,3,4,5,6 } задати бінарне відношення, для кожної пари (x_i x_j) графіка якого виконується умова x_i = x_i+ x_j .

Вправа 11. Встановити властивості наступних відношень на множині Z:

а) x₁+ x₂ - парне; б) x₁+ x₂ ≤ 100; в) x₁/ x₂ - парне; г) x₁ x₂ - непарне.

Вправа 12. Властивості рефлективності, симетричності та транзитивності відношень не є незалежними.

Треба дати відповідь на такі запитання:

1. Чи може антисиметричне відношення не бути транзитивним?

2. Чи може рефлексивно відношення бути асиметричним?

Вправа 13. Перевірити виконання властивостей комутативності, дистрибутивності, асоціативності, доповнення та подвійного доповнення операцій над множинами S та Т із вправи 1.

Вправа 14. Перевірити результати виконання операцій об’єднання та перетину множин S та Т вправи 1, коли в якості одного з операндів виступає множина U чи Ø.

Вправа 15. Задати відношення часткового порядку на множині:

1) A = {a₁, a₂, a₃, a₄, a₅, a₆} ; 2) B = {b₁, b₂, b₃, b₄, b₅, b₆};

3) C = {c₁, c₂, c₃, c₄, c₅, c₆}; 4) D = {d₁, d₂, d₃, d₄, d₅, d₆};

5) E = {e₁, e₂, e₃, e₄, e₅, e₆}; 6) F = {f₁, f₂, f₃, f₄, f₅, f₆};

7) G = {g₁, g₂, g₃, g₄, g₅, g₆}; 8) H = {h₁, h₂, h₃, h₄, h₅, h₆};

9) I = {i₁, i₂, i₃, i₄, i₅, i₆}; 10) J = {j₁, j₂, j₃, j₄, j₅, j₆};

11) K = {k₁, k₂, k₃, k₄, k₅, k₆}; 12) L = {l₁, l₂, l₃, l₄, l₅, l₆};

13) M = {m₁, m₂, m₃, m₄, m₅, m₆};14) N = {n₁, n₂, n₃, n₄, n₅, n₆};

15) P = {p₁, p₂, p₃, p₄, p₅, p₆}; 16) R = {r₁, r₂, r₃, r₄, r₅, r₆}.

Приклад: Множина S = {s₁, s₂, s₃, s₄, s₅, s₆}.

Відношеня:

α₁= {(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₁,s₂),(s₁,s₃),(s₁,s₄),(s₁,s₅),(s₁,s₆),(s₂,s₃),(s₂,s₄),(s₂,s₅),(s₂,s₆),(s₃,s₄), (s₃,s₅),(s₃,s₆),(s₄,s₅),(s₄,s₆),(s₅,s₆};

α₂= {(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₁,s₂),(s₁,s₃),(s₁,s₄),(s₁,s₅),(s₁,s₆),(s₂,s₄),(s₂,s₆),(s₃,s₅),(s₃,s₆),(s₄,s₆), (s₅,s₆};

α₃ = {(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₁,s₂),(s₂,s₃),(s₁,s₃)};

α₄= {(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₁,s₂),(s₁,s₃),(s₂,s₃),(s₄,s₅),(s₄,s₆),(s₅,s₆)}

є рефлексивними, антисиметричними, транзитивними; отже, ці відношення - відношення часткового порядку.

Слід звернути увагу, що для заданих відношень часткового порядку не обов’язково упорядковувати кожну пару елементів множини. Необхідно тільки, щоб відношення мало властивості рефлективності, антисиметричності, транзитивності.

Вправа 16. Задати відношення часткового порядку на множині з вправи 15 так, щоб множина стала лінійно впорядкованою.

Приклад: Якщо множина S із вправи 15 - частково впорядкована відношенням α₁, то вона є лінійно впорядкованою.

Вправа 17. Задати частковий порядок на множинах із вправи 15 та встановити в одержаних частково впорядкованих множинах універсальні межі.

Приклад: Нехай на множині S задано відношення часткового порядку α₁. Тоді s₁ - нижня, s₆ - верхня універсальні межі частково впорядкованої множини. Дійсно, s₁ ≤ s_i, s₆  s_i для будь-якого s_i  S . Якщо на множині S задано відношення часткового порядку α₂, то s₁ та s₂ будуть нижньою та верхньою універсальними межами відповідно. Одночасно, якщо множина S частково впорядкована відношенням α₃ чи α₄, то вона універсальних меж не має.

Вправа 18. Задати відношення строгого порядку на множинах із вправи 15.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆ }. Відношення

α₅= {(s₁,s₂),(s₁,s₃),(s₁,s₄),(s₁,s₅),(s₁,s₆),(s₂,s₃),(s₂,s₄),(s₂,s₅),(s₂,s₆),(s₃,s₄),(s₃,s₅),(s₃,s₆), (s₄,s₅),(s₄,s₆),(s₅,s₆};

α₆ = {(s₁,s₂),(s₂,s₃),(s₁,s₃),(s₁,s₄),(s₂,s₄),(s₃,s₄),(s₅,s₆)}

є антирефлексивними, асиметричними, транзитивними, отже, відношеннями строгого порядку.

Вправа 19. Встановити мінімальні та максимальні елементи частково впорядкованих множин із вправи 15.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆ }. Якщо порядок заданий відношенням α₁ чи α₂, то мінімальний елемент - s₁, максимальний - s₆.

Якщо порядок заданий відношенням α₃ , то s₁, s₄, s₅, s₆ - мінімальні, а s₃, s₄, s₅, s₆ - максимальні елементи.

Вправа 20. Чи може решітка мати більш ніж один максимальний (мінімальний) елемент?

Вправа 21. Чи можна стверджувати, що будь-яка частково впорядкована множина з одним мінімальним та одним максимальним елементами є решіткою?

Вправа 22. Нехай S - частково впорядкована множина. Відомо, що будь-яку частково впорядковану множину можна занумерувати так, що для будь-яких двох її елементів: s_i та s_j (s_i < s_j) елемент s_i одержить строго менший номер. Довести, що твердження ''будь-яку частково впорядковану множину S можна занумерувати так, що якщо елемент s_i одержить номер строго менший номера елемента s_j, то s_i  s_j" у загальному випадку місця не має.

Вправа 23. На множині з вправи 15 задати відношення часткового порядку: а) з одним максимальним та одним мінімальним елементами; б) з двома мінімальними та одним максимальним елементами; в) з двома мінімальними та двома максимальними елементами; г) з одним мінімальним та двома максимальними елементами.

Вправа 24. Чи може один елемент частково впорядкованої множини одночасно бути й мінімальним, й максимальним елементами цієї множини?

Вправа 25. Задати частковий порядок на множинах із вправи 15 та встановити межі та грані для підмножини, яка містить: а) перший, третій та п’ятий елементи; б) другий, третій та четвертий елементи.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆} впорядкована за допомогою відношення α₁. Тоді для підмножини S_α = {s₁, s₃, s₅} верхні межі - s₅ , s₆, верхня грань - s₅, нижня межа та грань - s₁. А для підмножини S_б = {s₂, s₃, s₄} верхні межі - s₄, s₅, s₆, нижні - s₁, s₂, верхня грань - s₄, нижня - s₂. Нехай S впорядкована за допомогою відношення α₂. Тоді для підмножини S_α = {s₁, s₃, s₅} верхні межі будуть s₅, s₆, нижня межа - s₁, верхня грань - s₅, нижня - S₁. Для підмножини S_б = {s₂, s₃, s₄} верхня межа - s₆, нижня - s₁, верхня грань - s₆, нижня - s₁. Якщо S впорядкована за допомогою відношення α₃ чи α₄, то обидві підмножини верхніх та нижніх меж і граней не мають.

Вправа 26. На кожній множині вправи 15 задати відношення часткового порядку, яке визначає решітку, але не перетворює множину у лінійно впорядковану.

Вправа 27. Чи існує бінарне відношення на не порожній скінченій множині, яке не є ні рефлексивним, ні антисиметричним, ні іррефлексивним? Якщо відповідь позитивна, то навести приклад такого відношення.

Вправа 28. Чи існує бінарне відношення на не порожній скінченій множині, яке не є ні симетричним, ні асиметричним, ні антисиметричним? Якщо відповідь позитивна, то навести приклад такого відношення.

Вправа 29. Чи можна стверджувати, що

а) решітка - це частково впорядкована множина, яка має верхню та нижню грані для будь-якої своєї підмножини?

б) в решітці для будь-якої підмножини елементів існують верхня та нижня грані?

Вправа 30. Чи можна стверджувати, що решітка - це частково впорядкована множина, будь-які два елементи якої мають верхні та нижні межі? Якщо відповідь негативна, то навести приклад частково впорядкованої множини, яка містить хоч одну пару елементів, які мають верхні (нижні) межі, але не мають верхньої (нижньої) грані.

Вправа 31. Чи можна стверджувати, що решітка - це частково впорядкована множина, якій належать її універсальні межі? Якщо відповідь негативна, то навести приклад частково впорядкованої множини, яка містить свої універсальні межі, але не є решіткою.

Вправа 32. Частково впорядковані множини задані діаграмами Хассе. Необхідно встановити для кожної з частково впорядкованих множин, чи в вона решіткою. Якщо відповідь негативна, то обгрунтувати її.

Варіанти діаграм Хассе:

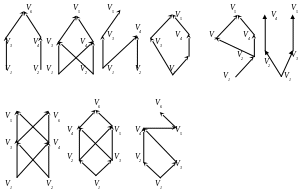
Вправа 33. Чи нема протиріччя у тому, що графік відношення часткового порядку, що визначає лінійно впорядковану множину, містить пари (r_i, r_i)?

Вправа 34. Чи можна стверджувати, що наявність пари елементів частково впорядкованої множини, які знаходяться у відношенні байдужості, дозволяє зробити висновок про те, що ця множина не є решіткою?

Вправа 35. Задати відношення еквівалентності на множинах із вправи 15.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆ }. Відношення

α₁= {(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₁,s₂),(s₂,s₁),(s₁,s₃),(s₃,s₁),(s₂,s₃),(s₃,s₂),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₄,s₅), (s₅,s₄),(s₄,s₆),(s₆,s₄),(s₅,s₆),(s₆,s₅)};

α₈ = {(s₁,s₁),(s₂,s₂),(s₁,s₂),(s₂,s₁),(s₃,s₃),(s₄,s₄),(s₃,s₄),(s₄,s₃),(s₅,s₅),(s₆,s₆),(s₅,s₆),(s₆,s₅)}

є рефлексивними, симетричними, транзитивними, отже, це відношення еквівалентності.

Вправа 36. Задати розбиття множин із вправи 15.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆}.

Розбиттям є множина підмножин S₁ = {s₁, s₂, s₃ }, S₂ = {s₄, s₅, s₆}. Дійсно, виконуються умови S₁  S₂ = {s₁, s₂, s₃, s₄, s₅, s₆} = S, S₁ ∩ S₂ = Ø. Множина підмножин S₃ = {s₁, s₂}, S₄ = {s₃, s₄}, S₅ = {s₅, s₆} теж є розбиттям. Дійсно, виконуються умови (S₃  S₄ )  S₅ = {s₁, s₂, s₃, s₄, s₅, s₆} = S ; S₃ ∩ S₄ = Ø, S₃ ∩ S₅ = Ø, S₄ ∩ S₅ = Ø.

Ще один приклад розбиття становить множина підмножин S₆ = {s₁}, S₇ = {s₂}, S₈ = {s₃}, S₉ = {s₄}, S₁₀ = {s₅}, S₁₁= {s₆}. Дійсно, легко перевірити, що множини S₁,...,S₆ попарно не перетинаються, а ((((S₆  S₇ )  S₈)  S₉ )  S₁₀ )  S₁₁ = {s₁, s₂, s₃, s₄, s₅, s₆} = S.

Вправа 37. Для відношень еквівалентності, заданих на множинах вправи 15, побудувати визначені ними розбиття.

Приклад: Нехай S = {s₁, s₂, s₃, s₄, s₅, s₆}. Тоді відношення еквівалентності α₁, задане на множині S, визначає розбиття {S₁, S₂}, де S₁ = {s₁, s₂, s₃}, S₂ = {s₄, s₅, s₆}. При формуванні підмножин розбиття включаємо в неї елементи s_i та s_j тоді і тільки тоді, коли в α₁ є пара (s_i, s_j).

Використовуючи цей спосіб, побудуємо розбиття для відношення α₈. Вибираємо довільний елемент із S, наприклад s₁. Включаємо його в підмножину S₃. Оскільки в α₈ існує пара {s₁, s₂}, включаємо в S₃ елемент s₂. Таким чином, підмножина S₃ = {s₁, s₂}.

Із елементів, не включених в S₃, вибираємо довільний, наприклад, s₃ і включаємо його у наступну підмножину розбиття S₄ . Оскільки α₈ містить пару {s₃, s₄}, то включаємо в S₄ елемент s₄. Відношення α₈ не містить пар, у яких би поруч з елементом s₃ чи s₄ були елементи, які від них відрізняються. Тому підмножина S₄ містить тільки ці два елементи. Вибираємо наступний елемент множини S, якого немає у побудованих підмножинах розбиття, наприклад s₅. Міркуючи аналогічно, встановимо останню підмножину S₅ = {s₅, s₆} розбиття.

У вправі 36 доведено, що система підмножин S₃, S₄, S₆ становить розбиття.

Вправа 38. Для розбиттів, заданих на множинах вправи 15, побудувати відповідні відношення еквівалентності.

Приклад: Нехай на множині S задано розбиття < S₁, S₂>. Відношення еквівалентності, що визначає це розбиття, одержимо, якщо в його графік включимо ті і тільки ті пари елементів із множини S, які належать до однієї підмножини розбиття.

Отже, S₁ = {s₁, s₂, s₃}, S₂ = {s₄, s₅, s₆}. Тоді у графік відношення включаємо такі пари:

{(s₁,s₁),(s₂,s₂),(s₃,s₃),(s₁,s₂),(s₂,s₁),(s₁,s₃),(s₃,s₁),(s₂,s₃),(s₃,s₂),(s₄,s₄),(s₅,s₅),(s₆,s₆),(s₄,s₅),(s₅,s₄), (s₄,s₆),(s₆,s₄),(s₅,s₆),(s₆,s₅)}/

Легко встановити, що одержаний графік – це графік відношення еквівалентності.

Вправа 39. В шафі у Віні Пуха m полиць, на кожній з яких можна розмістити k горщиків. Скількома різними способами можна розставити горщики на полицях, коли ми маємо необмежену кількість горщиків.

Розв’язок: На першій полиці ми можемо розставити горщики k+1 способами, включаючи варіант, коли на полиці не стоїть горщиків взагалі.

На другій полиці, незалежно від першої, ми можемо розставити горщики теж k+1 способами. Отже, якщо б ми мали 2 полиці, то виходячи з принципу суми, горщики можна розставити k+1+k+1=2(k+1) способами.

Ми маємо m полиць, тому розставити k горщиків на них можна m(k+1) способами.

Вправа 40. Обчислити, скількома способами можна здійснити такі дії: розділити 6 конспектів з дисципліни “Основи дискретної математики” між трьома студентами, яким однаково, які конспекти будуть у них.

Розв’язок: Першому студенту ми можемо дати від 0 до 6 конспектів (7 способів). Якщо першому ми дали n конспектів, то другому ми можемо роздати конспекти, що залишились 7-n способами. Порахуємо кількість способів. На кожний спосіб для першого студента маємо 7, 6, 5,...,1 способів на другого і третього:

0	6	0
0	5	1
0	4	2
...	...	...
0	0	6
1	5	0
1	4	1
...	...	...
1	0	6
...	...	...
6	0	0

Отже роздати 6 конспектів 3 студентам можна 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 способами.

Вправа 41. Є колода карт чотирьох мастей по

1. 9 номерів;

2. n номерів у кожній. Обчислити, скількома способами можна здійснити наступні вибірки:

1. 9 карт із послідовними номерами

2. стріт однієї масті (тобто послідовні чотири карти)

3. каре (чотири карти різної масті але однаковими номерами)

4. 2 каре і ще одну карту

5. одну трійку та одну двійку

6. одну трійку і ще дві довільні карти

Розв'язки:

1. “9”. Для колоди з дев'яти карт маємо:

Перша карта: одна з чотирьох можливих (1Т, 1П, 1Ч, 1Б).

Друга карта: одна з чотирьох можливих (2Т, 2П, 2Ч, 2Б).

…

Дев'ята карта: одна з чотирьох можливих (9Т, 9П, 9Ч, 9Б).

Отже, згідно принципу добутку, усього 4⁹ способів.

“n”. Для n карт маємо лише таке доповнення: дев'ята може розпочинатися з якогось номера від 1 до (n-8) включно. Тому, згідно принципу суми, маємо 4⁹ + 4⁹ +…+ 4⁹ = 4⁹ (n-8)

2. Стріт може розпочинатись з номера від 1 до (n-9) включно. Тому стрітів одної масті може бути (n-3), а будь-якої масті 4*(n-3). Для “9” номерів: 4*6 = 24.

3. У всій колоді маємо усього n каре. Вибирай – не вибирай, а лише n способів…

Для “9”: 9.

4. Одне каре ми можемо вибрати n способами. Ще одне каре – вже (n-1) способами. Отже два каре, згідно принципу добутку, можемо отримати n(n-8) способами.

В колоді залишилося (4n-8) карт. Отже, ще одну карту можна вибрати ще (4n-8) способами. Тому відповідь: n(n-8)(4n-8) способів.

“9”: 2016 способів.

5. Одну трійку з каре ми можемо вибрати 4-ма способами (ТПЧ, ТПБ, ПЧБ, БЧТ)

Одну двійку з каре – 6-ма способами (ПТ, ПЧ, ПБ, ТЧ, ТБ, ЧБ).

Отже, одну трійку з всієї колоди можна вибрати 4n способами (принци добутку: n способів – вибір каре, 4 способи – трійка з каре). Залишилося ще (n-1) номерів, з яких ми можемо вибрати двійку, тобто ще 6(n-1) способів.

За принципом добутку усього маємо 24n(n-1) способів.

“9”: 1728.

6. Одну трійку можна вибрати 4n способами. Залишається ще (4n-3) карти. Одну карту можна вибрати (4n-3)-ма способами. Ще одну - (4n-4)-ма способами.

Всього – 4n(4n-3)(4n-4) способами.

“9”: 38016 способів.

Вправа 42. На свій день народження Карлсон отримав 8 тортів з однією свічкою від чотирьох друзів. Обчислити кількість варіантів того, хто скільки тортів подарував, якщо:

1. Один з друзів подарував рівно один торт.

2. Один з друзів подарував не менше 5 тортів.

3. Двоє друзів подарували однакову кількість тортів.

Розв'язки:

1. Якщо один з друзів подарував 1 торт, то інші три – 7 тортів (свічку не рахуймо). Отже, маємо задачу про конспекти ! з тією лише різницею, що кожен друг подарував хоча б один торт.

II	III	IV
1 т	5 сп.
2 т	4 сп.
…	…	…
5 т	1 сп.

Усього 1 + 2 + 3 +4 + 5 = 15 способів.

2. Якщо один з друзів подарував більше ніж 6 тортів, знайдеться друг, котрий не подарував жодного торта, чого не може бути за умовою. Отже один з друзів подарував рівно 5 тортів. Тому інші три торти діляться між іншими трьома друзями по торту на кожного. В результаті – один спосіб.

I	II	III	IV
1 т	1 т	5 сп. розподілу
2 т	2 т	3 сп. розподілу
3 т	3 т	1 сп. розподілу

Усього 5 + 3 + 1 = 9 способів розподілу.

Скільки існує п’ятизначних чисел хоча б з однією п’ятіркою (число в десятковому записі і перша цифра не 0).

Ломовий розв’язок:

1. Порахуємо кількість п’ятизначних чисел з п’ятіркою на першій позиції і без п’ятірок на всіх інших позиціях. Зробимо це з правила добутку. На кожній позиції, окрім першої, може стояти 9 різних цифр (від 0 до 9, виключаючи 5), отже для кожної цифри на якійсь одній позиції може стояти в свою чергу 9 різних цифр на іншій, тобто за правилом добутку на двох позиціях може стояти 9*9=9² варіантів. Аналогічно для 4 позицій, що залишилися – 9⁴. Тобто маємо 9⁴ чисел.

2. Порахуємо кількість чисел з п’ятіркою на другій, третій тощо позиціях теж без п’ятірки на інших позиціях. Маємо 8*9³*4.

3. Далі потрібно було б порахувати кількість чисел з двома п’ятірками, потім з трьома і так далі, а потім скласти отримані кількості чисел, включаючи, навіть варіант, коли число складається повністю з п’ятірок.

Але якщо навіть якщо рахувати кількість чисел з двома п’ятірками на різних позиціях, то нам буде потрібно розглядати 4+3+2+1=10 варіантів їх розташування. Отже такі підрахунки ми будемо проводити до наступного понеділка включно, тому розглянемо

Вишуканий розв’язок:

Знайдемо кількість всіх п’ятизначних чисел без п’ятірок, таких, що на першій позиції не стоїть 0. Маємо 8*9⁴ чисел. Всього п’ятизначних чисел 9*10⁴. Отже, п’ятизначних чисел хоча б з однією п’ятіркою 9*10⁴ - 8*9⁴.

Вправа 43. Турнір шахістів. В фіналі турніру шахістів з армії зустрілися представники восьми військових звань: полковник, майор, капітан, лейтенант, старшина, сержант, єфрейтор і солдат. Всі з різних родів військ: один піхотинець, другий льотчик, потім танкіст, артилерист, кавалерист, мінометник, сапер і зв'язковий.

Поміркувавши, можна визначити військову спеціальність кожного з восьми шахістів згідно таких даних:

1. В першому турі полковник грав з кавалеристом.

2. Льотчик не грав в першому турі.

3. В другому турі піхотинець грав з єфрейтором.

4. В другому турі майор грав зі старшиною.

5. Після другого туру капітан вибув з турніру.

6. Через це в третьому турі не приймав участі сержант.

7. Через це в четвертому турі не приймав участі танкіст.

8. Через це в п'ятому турі не приймав участі майор.

9. В третьому турі лейтенант грав з піхотинцем.

10. В третьому турі полковник грав з артилеристом.

11. В четвертому турі сапер грав з лейтенантом.

12. В четвертому турі старшина грав з полковником.

13. Після шостого туру догравалась партія кавалериста з мінометником.

Для вирішення цієї задачі не обов’язково вміти грати в шахи. Потрібно лише знати, що в турнірі один і той же шахіст двічі вихідним не буває і з кожним партнером грає одну партію. Чи є зайві факти в умові задачі?

Розв'язок: Побудуємо таблицю всіх фактів, які стосуються військових, розміщуючи у відповідних клітинках таблиці номери, з яких випливає виключення можливості даної комбінації:

	Піхотинець	Льотчик	Танкіст	Артилерист	Кавалерист	Мінометчик	Сапер	Зв'язковий
Полковник	9-10	1-2	7-12	10	1	1-13	11-12	*
Майор	3-4	-	7-8	*	-	-	-	-
Капітан	5-9	*	5-7	5-10	5-13	5-13	5-11	-
Лейтенант	9	-	7-11	9-10	*	-	11	-
Старшина	3-4	-	7-12	10-12	1-12	*	11-12	-
Сержант	6-9	-	6-7	6-10	-	-	*	-
Єфрейтор	3	-	*	-	-	-	-	-
Солдат	*	-	-	-	-	-	-	-

Зірочки вказують спеціальності учасників турніру.

В таблиці зареєстровано 28 фактів, які випливають з умови задачі, а кількість фактів, необхідних для розв'язку даної задачі, також дорівнює 28 (7+6+5+4+3+2+1=28). Тобто зайвих фактів в умові задачі немає.

Вправа 44. Підрахувати кількість способів, якими можна з 28 кісток доміно вибрати дві так, щоб деяка кількість очок була на обох кістках.

Вправа 45. До роздоріжжя підїхав загін із п лицарів, причому l - ні в якому разі не поїдуть далі направо, r – наліво, s – прямо, а решті байдуже (l+r+s < n). Підрахувати кількість різних способів, якими лицарі можуть розбитися на три загони для подальшої подорожі.

Вправа 46. Нехай n=p₁^m1p₂^m2…p_k^mk – розклад натурального n на прості дільники p_1, p_2,… p_k. Обчислити

1/ кількість усіх дільників числа п

2/ кількість дільників числа, що не діляться на жодний з квадратів натуральних, крім 1

Вправа 47. Шість різних зірок записують по чотирьох різних каталогах. Обчислити кількість вариантів розкладання, що задовольняють умову:

1/ у першому каталозі немає зірок,

2/ у першому каталозі рівно одна зірка ,

3/ у першому каталозі не більше однієї зірки,

4/ у першому каталозі рівно дві зірки,

5/ у першому каталозі не менше двух зірок,

6/ у першому і другому катологагах рівно по одній зірці.

Вправа 48. Підрахувати кількість 7-цифрових кодів на кодовому замку, які:

1/ починаються з 2,

2/ закінчуються на 00, при умові, що номери не починаються з 8, 0 і 1,

3/ мають принаймні дві однакові сусідні цифри,

4/ мають рівно три однакові сусідні цифри,

5/ мають рівно чотири однакові сусідні цифри.

Вправа 49. Є необмежена кількість перлин рожевого кольору, що будуть розкладатися по кошиках не більше, ніж по n у m різні кошики. Скількома способами це можна зробити?

Вправа 50. Перестановки з повтореннями

1) Обчислить кількість слів довжини pq у р-літерному алфавіті, в яких кожна буква зустрічається q разів.

2) Обчислить кількість перестановок літер слова:

• математика;

• Місісіпі;

• Дніпропетровська;

• Бранденбург (літери “Б” і ”б” вважати однаковими);

• Абракадабра

3) Обчислить кількість способів, якими m-елементна можина розбивається на n підмножин, у першій з яких K₁ елементів, у другій-K₂,…, у останній - Kn.

4) Коли з 52 карт роздається 4-м гравцям по 13 карт. Обчисліть кількість способів такої роздачі.

5) У грі у преферанс колода з 32 карт роздається 3-м гравцям по 10 карт і 2 карти йдуть у прикуп. Обчисліть кількість способів такої роздачі.

Вправа 51. Вказати мінімальні, максимальні, найменші, найбільші елементи у частковому упорядкуванні R множини А = {1,2,3,4,5,}, а також множини верхніх граней підмножини В. При заданні R вважаеться, що з кожними двома парами вигляду (х,у), (у,z) воно містить також і пару (x,z), яка не записується.

1) R = і_АƯ{(1,2),(1,3),(1,4),(5,2)}, В = {1,5};

2) R = і_АƯ{(1,2),(1,3),(1,4),(5,2)}, В = {2.3};

3) R = і_АƯ{(1,2),(1,3),(4,1),(5,1)}, В = {1};

4) R = і_АƯ{(1,2),(1,3),(4,1),(5,1)}, В = {2,3};

5) R = і_АƯ{(1,2),(1,3),(1,4),(5,2)}, В = {4,5};

6) R = і_АƯ{(1,3),(2,3),(2,4),(3,5),(4,5)}, В = {3,4};

7) R = і_АƯ{(1,3),(2,3),(2,4),(3,5),(4,5)}, В = {3};

8) R = і_АƯ{(1,3),(2,3),(2,4),(3,5),(4,5)}, В = {1,2};

9) R = і_АƯ{(1,3),(2,3),(2,4),(3,5),(4,5)}, В = {5};

Вправа 52. Нехай відношення <, ≤ на множині Р визначені, як звичні упорядкування. Довести:

1) < o < ≠ <;

2) ≤ o < = <;

3) < o < ≠ <;

4) < o ≤ = <;

5) > o < ≠ P²;

6) > o ≤ ≠ P²;

7) < o > ≠ P²;

8) ≤ o < ≠ P².

Вправа 53. Довести, що відношення і_А є відношенням часткового порядку на множині А.

Вправа 54. Нехай на множині Р = {0,1,2…} визначено a ≤ b  а ділить b. Вважаємо, що 0 ділить 0. Довести, що ≤ є відношенням часткового порядку. Які елементи є мінімальними та максимальними у цьому упорядкуванні на множині:

1) N;

2) N/ {0};

3) N/ {0,1}.