Тема 1.2. Лінгвістичні моделі дискретної математики.

[1, гл.0. розд.2; гл.1. розд.1, § 1, 2; гл.2. розд.1, § 1, 2, 4; 4, гл.16. § 7-А; 20. ч.1, гл.4; 26, гл.3, § 3. 1] .

Вказівки щодо використання літературних джерел.

При вивченні матеріалу цього розділу необхідно звернути увагу на такі аспекти:

І) інформаційні процеси в системах управління можуть бути реалізовані тільки на базі будь-якої мови, що породжує проблеми використання мов;

2) основні проблеми дослідження мов:

- описання мови (синтаксис);

- забезпечення передачі смислу повідомленням на мові (семан­тика);

- забезпечення корисності повідомлення, що передається, для одержувача (прагматика).

Почати вивчення матеріалу рекомендується з аналізу природної мови, проблем її синтаксису, семантики ї прагматики, потім перей­ти до проблем дослідження штучних мов. Вивчення формальних мов (базові поняття, операції, способи визначення тощо) доцільно супроводжувати прикладами відомих мов, в першу чергу природних мов та мов програмування.

Для природної мови, якщо визначити її формально як підмножину множини слів у алфавіті, у вигляді слова виступає речення, а символом алфавіту треба прийняти слово, хоча морфологія починає будову слів із літер.

Зручно користуватися відомими прикладами, щоб показати важли­вість синтаксису, семантики, морфології, прагматики для мовних процесів. Розглянемо два відомі приклади С.Осуга. Нехай задана множина {     } її можна назвати мовою (формально), але зрозуміти не можна. Адже у нас немає уявлень про ці знаки як символи або літери.

Нехай слово використовує букви української мови, проте не завжди можна сказати, що речення написане цією мовою, оскільки неможливо виділити слова з літер, наприклад: “созкун телеяма ноховонера даїться, ботас фонгунет”.

Ліквідувавши цей недолік, ми, проте, не гарантовані від не­розуміння, якщо складемо слово без урахування синтаксису мови, наприклад: “телефон до хочу не. Ямада, - але додзвонитися кун працює”.

Граматично (або синтаксично) бездоганні речення можуть бути позбавлені змісту, про що свідчить приклад академіка Щерби: “Круглий квадрат солодко наспівує”.

Прагматичний аспект найкраще зрозуміє студент, який підготу­вав до екзамену всього одну тему, порівнюючи перед тим, як брати білет, два повідомлення: “В Австралії сьогодні дощ” і “Білет з підготовленою темою лежить зверху”.

Формальні мови варто задавати різними способами, порівнюючи їх; особливу увагу слід приділити аналізу алгебраїчного підходу, розпізнавачів і граматик. Аналіз відповідності розпізнавачів і граматик потрібно починати з графа переходу без петель і циклів, обмежуючись правилами породження типу d_i  e_id_j або d_i  e_i. Потім додавати петлі, цикли і т.п.

Регулярні множини широко використовуються в теорії мов. Вони визначаються так званим рекурсивним способом, що дозволяє побудувати всі об’єкти, які ми хочемо віднести до тих, що визна­чаються, і ніякі інші. Для дискретної математики, що розробляє моделі і конструктивні методи розв’язання практичних задач, це типово.

Визначення регулярної множини в алфавіті Е = {e₁, …, e_n}:

1) вводимо висхідні регулярні множини в алфавіті E: , {}, {e₁}, …, {e_n};

2) вводимо спосіб утворення інших рекурсивних множин з раніше отриманих /ми можемо це дозволити, оскільки ввели деякі регуляр­ні множини в пункті ї визначення/: якщо A і B - регулярні мно­жини в алфавіті E , то множини A  B, AB, A* - також регу­лярні / , , * - операції відповідно об’єднання, конкатена­ції, ітерації/;

3) немає інших регулярних множин в алфавіті E, крім визна­чених у п.п.1 і 2.

Приклади операцій наведені для вправи 1 теми 1.2, приклади ре­гулярних множин - для вправи 17 теми 1.2. Регулярні вирази вводяться для зручності позначення регулярних множин. Приклади побудови ре­гулярних виразів за регулярними множинами наведені для вправи 18 теми 1.2.

У підручнику [20] рекомендується ознайомитися з матеріалом гл.4. У разі нестачі часу можна зосередитися тільки на підрозділі “Концепція інтелектуальної комунікації”.

Вправи до теми 1.2.

Вправа 1. Нехай задано алфавіт D та алфавіт E.

Необхідно:

1) задати мову L₁ в алфавіті D та мову L₂ в алфавіті D довільним способом (крім мов Ø та {ε});

2) виконати операції композиції, конкатенації над мовами L₁ та L₂ та операцію ітерації над результатом виконання операції композиції.

Варіанти задання алфавітів:

1) D = {a₁, a₂, a₃}, E = {1,2,3}; 2) D = {b₁, b₂, b₃, b₄}, E = {0,1};

3) D = {c₁, c₂, c₃}, E = {p₁, p₂, p₃, p₄}; 4) D = {f₁, f₂, f₃}, E = {r₁, r₂, r₃};

5) D = {g₁, g₂}, E ={s₁, s₂, s₃, s₄}; 6) D = {h₁,h₂, h₃}, E = {0,1,2,3};

7) D = {8, 9}, E = {t₁, t₂, t₃, t₄}; 8) D = {i₁, i₂, i₃}, E = {4,5,6,7}.

Приклад: Нехай D = {d₁, d₂, d₃, d₄}, E = {e₁, e₂, e₃, e₄}/

Мова L₁ - в алфавіті D: L₁ = {ε, d₁ d₂, d₂ d₃, d₃ d₄}.

Мова L₂ - в алфавіті E: L₂ = {e₁, e₂ e₃, e₁ e₃ e₄ }.

Результати виконання операцій:

• композиції L₁ та L₂:

L₁  L₂ = {ε, d₁ d₂, d₂ d₃, d₃ d₄, e₁, e₂ e₃, e₁ e₃ e₄ };

• конкатенації L₁ та L₂:

L₁ L₂ = {e₁, e₂ e₃, e₁e₃e₄, d₁d₂ e₁, d₁d₂ e₂ e₃, d₁d₂ e₁e₃e₄ , d₂d₃ e₁, d₂d₃ e₂e₃, d₂d₃ e₁ e₃e₄, d₃d₄ e₁, d₃ d₄ e₂ e₃, d₃d₄e₁e₃e₄};

• ітерації:

{L₁  L₂}^* = {L₁  L₂}ⁿ,

{L₁  L₂ }⁰ = {};

{L₁  L₂}¹ = {ε, d₁ d₂, d₂ d₃, d₃ d₄, e₁, e₂ e₃, e₁ e₃ e₄ };

{L₁  L₂}² = {L₁  L₂} {L₁  L₂}¹ = {ε, d₁ d₂, d₂ d₃, d₃ d₄, e₁, e₂ e₃, e₁ e₃ e₄, d₁ d₂ d₁ d₂, d₁ d₂ d₂ d₃, d₁ d₂ d₃ d₄, d₁ d₂ e₁, d₁ d₂ e₂ e₃, d₁ d₂ e₁ e₃ e₄, d₂ d₃ d₁ d₂, d₂ d₃ d₂ d₃, d₂ d₃ d₃ d₄, d₂ d₃ e₁, d₂ d₃ e₂ e₃, d₂ d₃ e₁ e₃ e₄, d₃ d₄ d₁ d₂, d₃d₄d₂ d₃, d₃ d₄ d₃ d₄, d₃ d₄ e₁, d₃ d₄ e₂ e₃, d₃ d₄ e₁ e₃ e₄, e₁ d₁ d₂, e₁ d₂ d₃, e₁ d₃ d₄, e₁e₁, e₁ e₂ e₃, e₁ e₁ e₃ e₄, e₂ e₃d₁d₂, e₂ e₃ d₂ d₃, e₂ e₃ d₃ d₄, e₂ e₃ e₁, e₂ e₃ e₂ e₃, e₂ e₃ e₁ e₃ e₄ , e₁ e₃ e₄ d₁ d₂, e₁ e₃ e₄ d₂ d₃, e₁ e₃ e₄ d₃ d₄, e₁e₃e₄e₁, e₁e₃e₄e₂e₃, e₁ e₃ e₄ e₁ e₃ e₄}

і т.д.

{L₁  L₂}ⁿ = {ε, d₁ d₂, d₂ d₃, d₃ d₄, e₁, e₂ e₃, e₁ e₃ e₄ , …}.

Позитивна ітерація мови {L₁  L₂} визначається так:

{L₁  L₂}⁺ = {L₁  L₂}ⁿ.

Вправа 2. Для слова а₁ а₂ а₃ а₄ вказати всі префікси, суфікси та підслова.

Вправа 3. Встановити залежність між множинами L^*, L⁺ та {ε} для довільної мови L в алфавіті D.

Вправа 4. Задати скінчену мову L₃ у алфавіті E = {0,1} та описати структуру її слів природною мовою. Необхідно прагнути до того, щоб при великій кількості слів у мові L₃ її описання природною мовою містило б якомога менш слів.

Приклад: Мова L₃ = {000, 001, 010, 100, 011, 101, 110, 111}. Її описання українською мовою: мова L₃ містить всі можливі послідовності символів 0 та 1 довжиною 3.

Вправа 5. Задати нескінченну мову L₄ в алфавіті E = {0,1} та описати структуру її слів природною мовою.

Приклад: мова L₄ = {0, 01, 011, 0111,...}. Її описання українською мовою: мова L₄ містить усі слова, першим символом яких є символ 0, за яким слідують довільна кількість символів 1.

Вправа 6. Задати іншим способом мову, яку породжує граматика

G = <{d₀, d₁}, {0,1}, P, d₀ >, де множина Р містить такі правила:

Варіант 1 Варіант 2 Варіант 3

d₀  1 d₁ d₀  1 d₁ 0 d₀  0 d₁ 0

d₁  1 d₁ d₁  1 d₁ 0 d₁  1 d₁ 1

d₁  ε d₁  ε d₁  ε

Варіант 4 Варіант 5 Варіант 6

d₀  d₁1 d₀  1 d₁ d₀  0 d₁ 1

d₁  d₁1 d₀  0 d₁ d₁  0 d₁

d₁  d₁0 d₁  0 d₁  1 d₁

d₁  ε d₁  1 d₁  ε

Варіант 7 Варіант 8 Варіант 9

d₀  d₁d₁d₁d₁ d₀  0 d₀ d₀  d₁ d₀ d₁

d₁  0 d₀  1 d₀ d₁  0 0

d₁  1 d₀  ε d₁  1 1

Приклад: Нехай множина Р містить такі правила:

d₀  0 1 d₁

d₁  0 1 d₁

d₁  ε

У такому разі граматика G породжує мову, кожне сово якої має вигляд 0101…01, де n = 1, 2, 3, ... .

n разів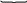

Дійсно, перше правило з множини Р завжди породжує першу пару 01, за якою з допомогою другого правила можна приєднати до вже отриманого слова довільну кількість пар 01, причому в будь-який час можна припинити процес приєднання до слова нових пар 01 за допомогою третього правила.

Вправа 7. Задати граматику, що породжує мову L₃ із вправи 4.

Вправа 8. Задати граматику, що породжує мову L₄ із вправи 5.

Вправа 9. Задати розпізнавач, який допускає всі слова ітерації об’єднання мов L₁ та L₂ вправи 1.

Вправа 10. Задати граматику, що породжує мову, яку допускає розпізнавач із вправи 9.

Вправа 11. Задати граматику, що породжує мову, яку допускає такий розпізнавач з скінченою кількістю станів: Р = < E, A, f₁, a₀, A₀ >, де E = {0,1} - множина вхідних символів, A = {a₀, a₁, a₂} - множина станів, f₁ - функція переходів, a₀ - початковий стан, A₀  A - множина заключних станів.

Варіанти функції переходів:

1) f₁(a₀ , 0) = a₀ ; 2) f₁(a₀ , 0) = a₁ ; 3) f₁(a₀ , 0) = a₂ ;

f₁(a₀ , 1) = a₁ ; f₁(a₀ , 1) = a₂ ; f₁(a₀ , 1) = a₁ ;

f₁(a₁ , 0) = a₁ ; f₁(a₁ , 0) = a₁ ; f₁(a₁ , 0) = a₂ ;

f₁(a₁ , 1) = a₂ ; f₁(a₁ , 1) = a₂ ; f₁(a₁ , 1) = a₁ ;

4) f₁(a₀ , 0) = a₁ ; 5) f₁(a₀ , 1) = a₀ ;

f₁(a₀ , 1) = a₂ ; f₁(a₀ , 0) = a₁ ;

f₁(a₁ , 0) = a₂ ; f₁(a₁ , 1) = a₁ ;

f₁(a₁ , 1) = a₀ ; f₁(a₁ , 0) = a₂ .

Заключний стан - a₂ .

Вправа 12. Задати іншим способом мову, яку допускає такий розпізнавач з скінченою кількістю станів Р = < E, A, f₁, a₀, A₀ >, де E = {0,1} - множина вхідних символів, А - множина станів, f₁ - функція переходів, a₀ - початковий стан, A₀  A - множина заключних станів.

Варіанти функції переходів та станів:

1) A = {a₁, a₂, a₃, a₄}, 2) A = {a₀, a₁}, 3) A = {a₀, a₁, a₂},

A₀ ={a₃, a₄}, A₀={a₁}, A₀={a₂}.

f₁(a₀ , 0) = a₁ ; f₁(a₀ , 1) = a₁ ; f₁(a₀ , 1) = a₀ ;

f₁(a₀ , 1) = a₂ ; f₁(a₁ , 1) = a₁ ; f₁(a₁ , 1) = a₂ ;

f₁(a₁ , 0) = a₃ ; f₁(a₂ , 1) = a₂ ;

f₁(a₁ , 1) = a₄ ;

f₁(a₂ , 0) = a₃ ;

f₁(a₂ , 1) = a₄ ;

4) A = {a₀, a₁}, 5) A = {a₀ , a₁, a₂, a₃, a₄, a₅, a₆};

A₀ = {a₁}, f₁(a₀ , 0) = a_1, f₁(a₂ , 1) = a₄

f₁(a₀ , 0) = a_1, f₁(a₀ , 1) = a_2, f₁(a₃ , 0) = a₅

f₁(a₁ , 0) = a_{1 ;} f₁(a₁ , 0) = a_{3 ,} f₁(a₃ , 1) = a₆

f₁(a₁ , 1) = a_4, f₁(a₄ , 0) = a₅

f₁(a₂ , 0) = a_3, f₁(a₄ , 1) = a₆ .

Вправа 13. Встановити пари граматик із вправи 6 та розпізнавачів із вправи 12, які визначають одну і ту ж мову.

Вправа 14. В алфавіті {А, Б, В} визначені мови:

1) L₁= {, AA, AAA, AAAA, …};

2) L₂ ={, AБ, AББ, AБББ, …};

3) L₃ ={, ВА, ВБ, АВ, АВАВ, АВАВАВ, …};

4) L₄ ={АА, АБ, ВА, БА, ВАА, БАА, ВААА, БААА, …};

5) L₅ ={, АБ, ААББ, АААБББ};

6) L ₆ ={А, АА, ААБ, ААВ, ААА};

7) L ₇={А, АБВ, АБВ, АБВ, АБВАБВАБВ, …};

8) L₈={, АБ, АВ, БАВ, БАВАВ, БАВАВАВ,…,Б, ББ, БББ,… };

9) L ₉={АБ…В, АБ…ВАБ…В, АБ…ВАБ…ВАБ…В,… };

10) L₁₀= {, А, Б, В, АА, АБ, АВ, БА, ББ, БВ, ВА, ВБ, ВВ, ААА, ААБ, ААВ, АБА, АББ, АБВ, АВА, АВБ, АВВ, БАА, БАБ, БАВ, ББА, БББ, ББВ, БВА, БВБ, БВВ, ВАА, ВАБ, ВАВ,ВБА, ВББ, ВБВ, ВВА, ВВБ, ВВВ,… };

11) L ₁₁= {АБ, АВ, АБАБ, АБАВ, АВАБ, АВАВ, АБАБАБ, АБАБАВ, АБАВАБ, АБАВАВ,

АВАБАБ, АВАБАВ, АВАВАБ, АВАВАВ,… };

12) L ₁₂ = {АА, АБ, ААА, АБАБ, АААААА, АБАБАБ, …};

13) L ₁₃ = {АБАБ, АБАБАБАБ, АБАБАБАБАБАБАБАБ,… };

14) L ₁₄ = {АБАБ, АБАБАБ, АБАБАБАБАБАБ, …};

15) L₁₅= {, А, Б, В, АА, ББ, ВВ};

16) L₁₆= {, АБ, АВ, АА, ААА, АААА,…}.

Необхідно задати кожну мову (іншим способом: а) граматикою, що її породжує; б) розпізнавачем, який її розпізнає).

Вправа 15. Які з граматик, наведених у вправі 6 теми 1.2, пород­жують регулярну мову.

Вправа 16. Навести приклад регулярної множини та кількох регу­лярних виразів, що відповідають їй.

Вправа 17. Установити, чи є регулярними такі множини в алфавіті {0,1}:

1) { 0, 1, 00, 01, 10, 11, 000, 001, 010, 100, 011, 101, 111,…};

2) { 01, 0101, 010101,…};

3) { 010, 0100, 01000,…};

4) { 010, 010010, 010010010,…};

5) { 1, 11, 01, 111, 101, 011, 1111, 1101, 0101, 0111, 11111, 11101, 10111, 10101, 01011,

011111, …};

6) { 1, 01, 11, 001, 011, 101, 111,…};

7) { 01, 001, 0001, 1001, 00001, 10001, 000001, 100001, 101001,…};

8) { 110, 1100, 11000,…};

9) { 0011, 00011, 000011,…};

10) { 01, 10, 0101, 1010, 010101, 101010,…};

11) {0, 1, 00, 11, 000, 111,…};

12) {0, 00, 000, 0000}.

Приклад: Покажемо, що множина слів в алфавіті {0,1} є регулярною:

X = {100, 0100, 1100, 00100, 01100, 11100, 000100, 001100, 011100, 111100, 101100, 0000100, 0001100, 0011100, 0111100, 0101100, 1111100, 1101100, 1010100,…}.

За визначенням, {0} та {1} - регулярні множини. Тоді регулярними множинами є: а) ітерації {0}* та {1}* ; б) конкатенація {0} {1}. Таким чином, регулярними є також конкатенації: {0}* {1} та {1}* {0}. Далі одержуємо конкатенацію {0}* {1} {1}* {0}, яка теж є регулярною. Наступний етап дає регулярні множини, одержані за допомогою однієї конкатенації :

{0}* {1} {1}* {0}{0} та {0}* {1} {1}* {0}{1} .

Як ітерація регулярної множини регулярна множина {{0}* {1} {1}* {0}{1}}*.

Тоді як конкатенація регулярних множин регулярна множина

{{0}* {1} {1}* {0}{1}}*.{0}* {1} {1}* {0}{0}.

Легко перевірити, що остання мно­жина збігається з Х . Таким чином, множина Х є регулярною.

Вправа 18. Знайти регулярні вирази для регулярних множин вправи 17. Для яких множин з вправи 17 існує кілька регулярних виразів, які не містять регулярних виразів  та .

Приклад: Розглянемо регулярну множину з попереднього прикладу. Ми одержала доведення її регулярності, показуючи, що вона утворюється за допомогою операцій конкатенації та ітерації над регулярними множинами {0} та {1} в алфавіті {0,1}:

{{0}*{1}{1}*{0}{1}}*{0}*{1}{1}*{0}{0}.

Використовуючи відповідність між регулярними множинами {0}, {1} та регулярними виразами відповідно 0 та 1, а також спосіб запису регулярних виразів для регулярних множин, одержаних за допомогою операцій конкатенації (01 для регулярних множин {0},{1}), ітерації {0}* та {1}* , записуємо регулярний вираз для регулярної множини, що розглядається:

((0)*1(1)*01)*(0)*1(1)*00.

Розглянемо множину варіанту 1 вправи 17. За визначенням регулярної множини, множини {0} та {1} регулярні в алфавіті {0,1}. Як результат операції об’єднання регулярних множин множина {0}  {1} регулярна. Як ітерація регулярних множин множина {{0}  {1}}* регулярна. Очевидно, остання множина збігається з множиною варіанту 1 вправи 17. Регулярний вираз для цієї множини (0+1)*. Але ту ж саму регулярну множину визначає регулярний вираз (1+0)*. Можна використовувати інші пари рівних регулярних виразів для одержання кількох регулярних виразів для однієї регулярної множини. Серед цих пар рівних регулярних виразів деякі побудовані без урахування властивостей регулярних множин {} та . Ці пари треба використовувати для виконання другої частини вправи.

Вправа 19. Чи всі скінченні множини є регулярними?

Вправа 20. Чи можливо у будь-якій регулярній множині знайти регулярну під множину?

Вправа 21.Чи можливо у будь-якій регулярній множині знайти підмножину, яка б не була регулярною? Якщо відповідь негативна, то потрібно конкретизувати умови, при виконанні яких у регулярній множині завжди можливо знайти нерегулярну підмножину.

Вправа 22. Перевірити регулярність множин із вправи 17 теми 1.2 та задати їх регулярними виразами.

Вправа 24. Перевірити послідовність символів та установити, чи є вона регулярним виразом для регулярних множин в алфавіті {0, 1}. Якщо відповідь негативна, треба дати пояснення, які правила утворення регулярних виразів порушені.

Якщо відповідь позитивна, то задати регулярну множину чи її початкові ланцюжки перелічуванням.

Варіанти послідовностей:

1) 01 + 10 + (00)*+ (11)*; 5) (0)*10(1)* + (10)*(01)* + ((101)*1)*;

2) 01 + 20 + (2)*1(0)*; 6) ()*( )*1(0)*1+1+(0+0)*1;

3) (01 + 02)*01 + (10)*; 7) (0 + 1)* + (1 + 0)*;

4) (0 +++  + 1)(0 + (1)*; 8) (0 + 0)* + (1 + 0)1(0 + 1).