
- •Вопрос 1. Модель capm и ее ценовое представление. Плата за рыночный риск и реальные инвестиции.
- •Вопрос 2. Место системы внутрифирменного планирования и управленческого учета в риск-менеджменте
- •Вопрос 3. Методы оценки рисков редких событий, показатели риска типа var. Их использование в банковской сфере
- •Вопрос 5. Постулаты capm и реальность. Ставка дисконта как темп падения двойственных оценок. Большой и малый проект, границы использования критерия npv.
- •Вопрос 6. Использование маржинальной теории и эффекта операционного рычага в управлении рисками.
- •Вопрос 7. Модели одномерных временных рядов с сезонной и циклической составляющей. Методы построения и прогнозирования.
- •1. По видам хозяйственной деятельности в соответствии с международными стандартами учета
- •2. По направленности движения денежных средств фирмы
- •3. По методу исчисления объема
- •4. По уровню достаточности объема
- •5. По методу оценки во времени
- •6. По непрерывности формирования в рассматриваемом периоде
- •7. По масштабам обслуживания хозяйственного процесса
- •Вопрос 10. Однофакторные стохастические процессы. Основные виды моделей. Выбор аналитической формы модели. Оценка параметров. Критериальная проверка качества.
- •Модели авторегрессии Общий вид модели ар(k):
- •Модели скользящего среднего
- •Модели авторегрессии-скользящего среднего
- •Вопрос 11. Корреляционно-дисперсионный анализ переменных, выраженными количественными и качественными показателями.
- •Вопрос 12. Структурные риски организации. Роль профессиональных рисков при исполнении обязательств компании. Кредитные риски организации.
- •Вопрос 13. Модели бинарного выбора (логит, пробит)
- •Вопрос 14.Математические модели на сетевых графиках и коммуникационных сетях в условиях определенности, риска и неопределенности. (по лекциям Косорукова)
- •Сетевые графики
- •Коммуникационные сети
- •Вопрос 15. Интегральные показатели эффективности. Npv, irr, pp, pi
- •Вопрос 16. Методология анализа страновых рисков ihs Energe Group. Методология анализа политических рисков компании beri.
- •Вопрос 17. Основные подходы к оценке эффективности мер по управлению рисками. В чем состоит различие подходов, основанных на соотношениях «затраты-выгода», «затраты-риск», «эффективность затрат».
- •Вопрос 18. Неопределенность и риск. Ожидаемая полезность. Неприятие риска и плата за риск, критерий.
- •Вопрос 20. Понятие риска в экономике. Подходы, принципы и методы оценки рисков. Меры рисков. Дисперсия как мера риска. Примеры оценки рыночных, финансовых, предпринимательских рисков.
- •Вопрос 22. Сущность и виды банкротства. Причины банкротства предприятий с позиции риск-анализа. Системы диагностики угрозы банкротства предприятия.
- •Вопрос 23. Использование финансово-экономического анализа для выявления рисков
- •Вопрос 24. Глобальные риски. Определение. Показатели тяжести. Основные проблемы управления глобальными рисками. Пути снижения глобальных рисков.
- •1. Масштабы и степень воздействия (последствия) глобальных рисков.
- •2. Природа воздействия - экономические или социальные, или оба типа рисков одновременно.
- •3. Неопределенность
- •4. Необходимость реагирования многих заинтересованных сторон (стейкхолдеров)
- •Вопрос 25.Особенности организации проектов в атомной энергетике, гидроэнергетике, строительной и нефтегазовой отрасли.
- •Вопрос 26. Модель социального движения населения. Краткое введение и условные обозначения
- •Модели социального движения
- •Модели социального движения с другими показателями социального движения (модифицированная модель социального движения)
- •Вопрос 27. Организационно–экономические механизмы управления охраной природы. Какие показатели выражают ущерб окружающей природной среде? Оценка стоимостных характеристик ущерба.
- •Вопрос 28. Сравнительный анализ процентного и кредитного риска.
- •Вопрос 29. Сущность затрат и расходов. Анализ безубыточности как инструмент управления финансовыми рисками. Использование маржинальной теории в управлении рисками.
- •Вопрос 30. Обоснование критерия npv для малых реальных проектов. Реальные и номинальные беты. Интервальная неопределенность и критерий Гурвица.
- •Вопрос 31. Анализ риска ликвидности и неплатежеспособности. Анализ ценового риска в портфеле производных финансовых инструментов.
- •Ликвидность как характеристика финансового состояния предприятия
- •Ликвидность бухгалтерского баланса
- •Вопрос 32. Чистые и спекулятивные риски. Особенности управления этими видами рисков в предпринимательской сфере. Критерии и постановки задач оптимального управления чистыми и спекулятивными рисками.
Вопрос 13. Модели бинарного выбора (логит, пробит)
В эконометрических моделях выбора зависимая переменная - вероятность проявления события – ставится в зависимость от уровня ряда факторов, влияющих на возможность его проявления, и (или) его параметров. Содержательное уравнение такой модели может быть представлено в следующем виде:
![]()
В зависимости от числа вариантов исходов события (альтернатив) для оценки их вероятностей могут использоваться эконометрические модели бинарного или множественного выбора.
Модели бинарного выбора
В моделях бинарного выбора результирующий показатель может принимать только два значения (1 – событие имело место, 0 – в противоположном случае).
Модели бинарного выбора могут использоваться при оценке вероятности проявления события в рамках биномиального закона. В их основе лежит предположение, что вероятность проявления события в определенный период времени зависит от ряда факторов (вероятность отказа техники зависит от степени ее износа, квалификации персонала, интенсивности загрузки и т.п., вероятность дефолта заемщика зависит от факторов, характеризующих уровень его финансовой устойчивости, кредитоспособности, стабильности рынка и т.д.). Отказ техники в течение какого-либо периода определяется событием y=1, безаварийная работа - y=0.
Исходными данными для построения такого рода моделей являются исходы рассматриваемого события и соответствующие им значения факторов. В случае сгруппированных данных они могут быть представлены в следующем виде:
 (1)
(1)
где
![]() ,
- характеризует r-е
значение наблюдаемой переменной (0 или
1) при i-ом
наборе значений объясняющих переменных
факторов.
,
- характеризует r-е
значение наблюдаемой переменной (0 или
1) при i-ом
наборе значений объясняющих переменных
факторов.
При этом допускается возможность, что один и тот же набор факторов может давать разные исходы.
Набор
переменных
![]() для каждого i
может быть приведен к частному виду.
Тогда данным i-й
строки, т.е. вектору
для каждого i
может быть приведен к частному виду.
Тогда данным i-й
строки, т.е. вектору
![]() ,
соответствует частота проявления
события
,
соответствует частота проявления
события
![]() ,
,
![]() (2)
(2)
где
![]() - общее число исходов события,
соответствующее i-му
набору факторов;
- общее число исходов события,
соответствующее i-му
набору факторов;
=0 или 1.
Модели
бинарного выбора оценивают вероятность
события (![]() )
при условии i-ого
набора факторов как некоторую функцию
распределения
)
при условии i-ого
набора факторов как некоторую функцию
распределения
![]() ,
зависящую от значений этих факторов и
соответствующих им параметров. При этом
функция
,
зависящую от значений этих факторов и
соответствующих им параметров. При этом
функция
![]() определена на отрезке [0;1] и обычно форма
взаимозависимости параметров
определена на отрезке [0;1] и обычно форма
взаимозависимости параметров
![]() - факторов
- факторов
![]() выбирается линейной, хотя последнее
предположение и не является обязательным.
Для выбранной формы взаимозависимости
между параметрами
выбирается линейной, хотя последнее
предположение и не является обязательным.
Для выбранной формы взаимозависимости
между параметрами
![]() и
можно ввести латентную, гипотетическую
переменную Z,
значения которой в случае линейной
формы определяются уравнением:
и
можно ввести латентную, гипотетическую
переменную Z,
значения которой в случае линейной
формы определяются уравнением:
![]() (3)
(3)
В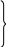 целом на функцию
целом на функцию
![]() накладываются следующие естественные
для функции распространения ограничения:
накладываются следующие естественные
для функции распространения ограничения:
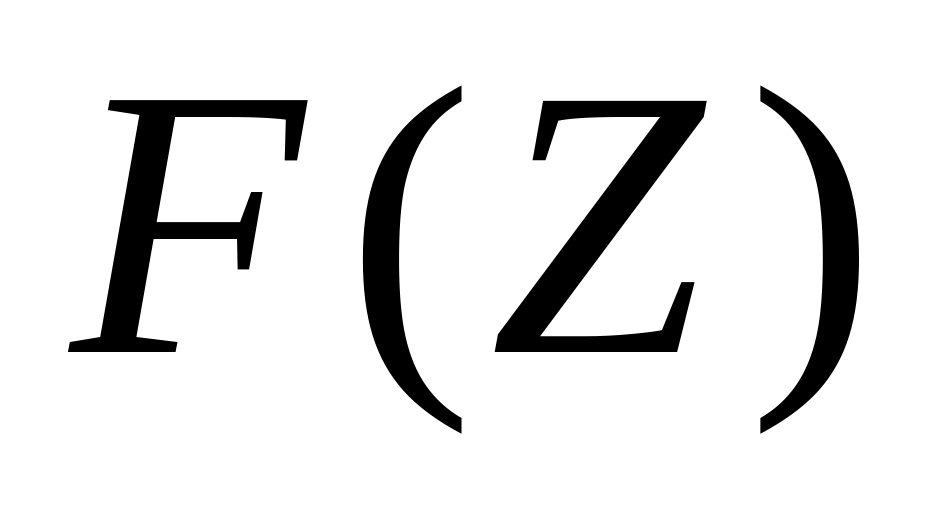 монотонно
возрастает с ростом Z
монотонно
возрастает с ростом Z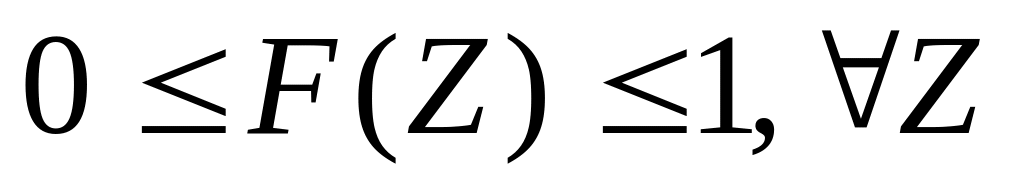 (4)
(4)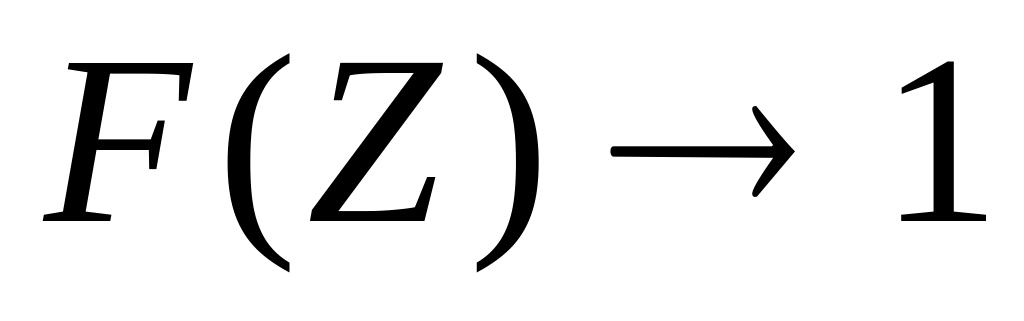 при
при

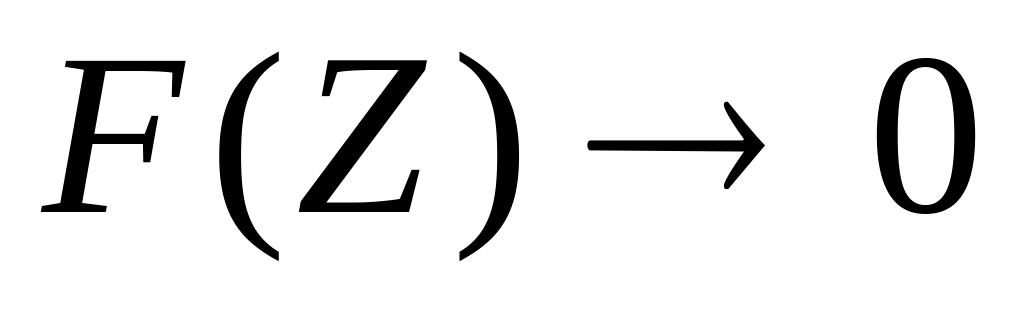 при
при
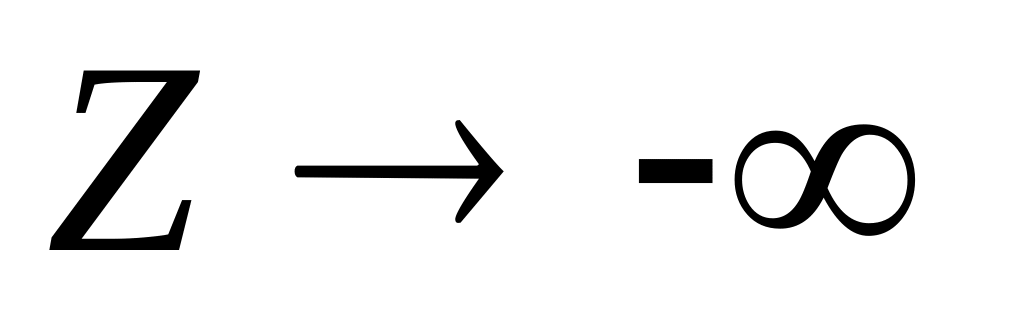
На практике среди моделей бинарного выбора наиболее широкое распространение получили пробит- и логит-модели. Пробит-модели используют в качестве функцию стандартного нормального распределения. Согласное ей вероятность проявления события при i-м наборе факторов определяется как
![]() (5)
(5)
где
![]() .
.
В логит-моделях функция имеет вид логистической функции
![]() (6)
(6)
Оба варианта функции распределения удовлетворяют условию (4) и обладают свойством симметрии относительно Z=0, т.е. F(-Z)=1-F(Z).
Для любого варианта представления относительная частота (выражение (2)) связывается со значением эконометрической зависимостью
![]() ,
(7)
,
(7)
в
которой неизвестными являются коэффициенты
![]() .
.
При
этом в соответствии с распределением
Бернулли ошибка
![]() имеет математическое ожидание, равное
нулю,
имеет математическое ожидание, равное
нулю,
![]() и дисперсию
и дисперсию
![]() ,
которая таким образом оказывается
зависимой от переменной
,
которая таким образом оказывается
зависимой от переменной
![]() .
Из этого вытекает, что модель (7) может
рассматриваться как эконометрическая
модель с гетероскедастическими ошибками.
.
Из этого вытекает, что модель (7) может
рассматриваться как эконометрическая
модель с гетероскедастическими ошибками.
Можно предложить несколько подходов к оценке параметров модели (7) , базирующихся на использовании метода максимального правдоподобия, нелинейного метода наименьших квадратов и их модификаций.
Согласно
нелинейному МНК требуется оценить
значения параметров
функции
![]() ,
при которых достигает минимума взвешенная
по дисперсии сумма квадратов ошибки
модели (7), имеющая следующий вид:
,
при которых достигает минимума взвешенная
по дисперсии сумма квадратов ошибки
модели (7), имеющая следующий вид:
![]() (8)
(8)
где в качестве функции используются функции, определенные выражениями (5) и (6).
Возможные процедуры оценивания, использующие нелинейный МНК, включают следующие этапы:
Выбор исходной точки начала расчетов, т.е. вектор
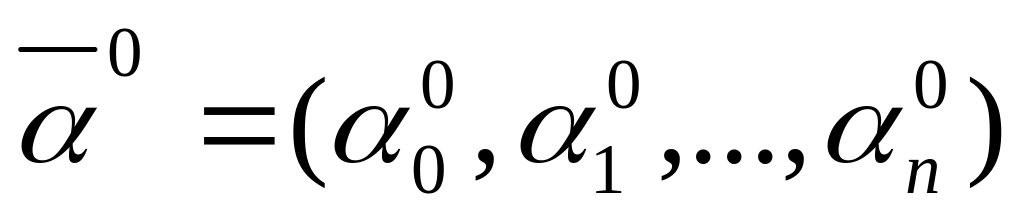
Выбор направления движения к точке оптимума по каждому из параметров, т.е. знака прироста параметра
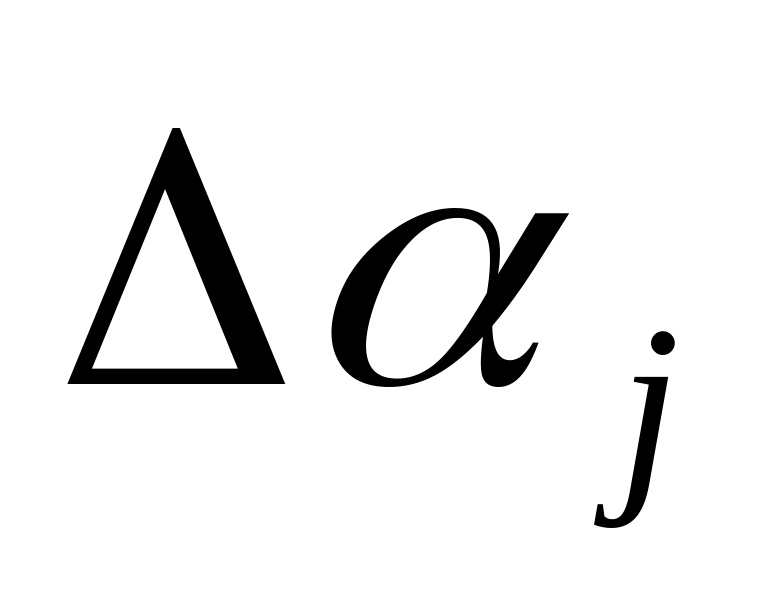 - «+» или «-»,
- «+» или «-»,
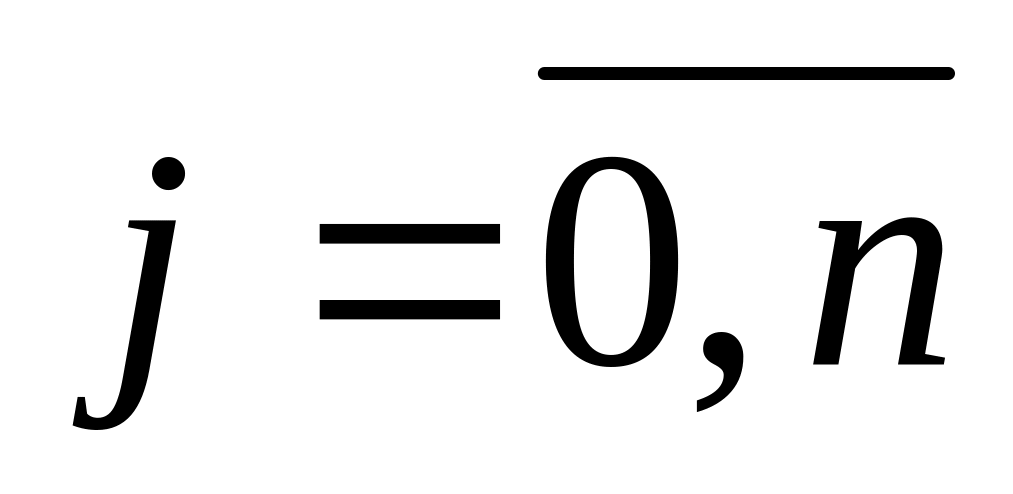
Выбор рациональной величины прироста
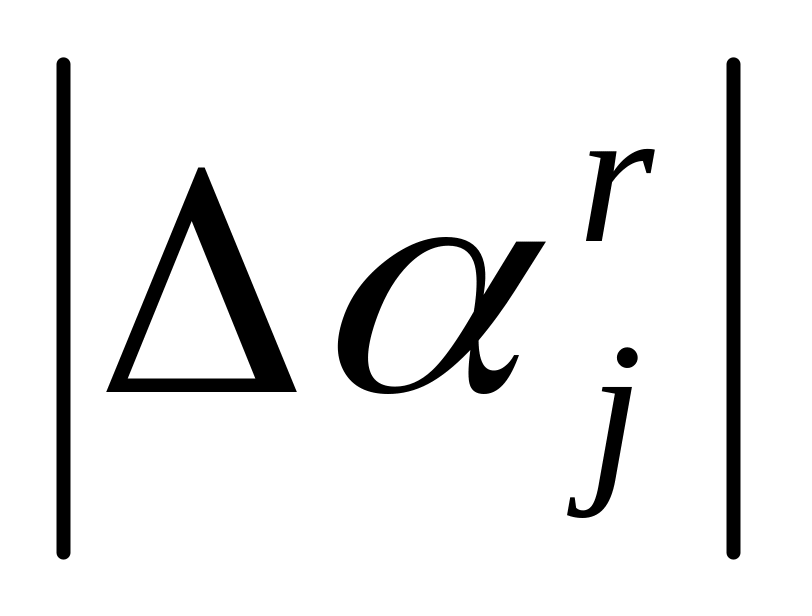 на r-ом шаге расчетов,
на r-ом шаге расчетов,
Среди
возможных процедур, используемых на
практике для оценки оптимальных значений
параметров
![]() ,
,
выделим процедуры, использующие
графический метод, методы линеаризации
функционала (метод Маркуардта) и др.
,
,
выделим процедуры, использующие
графический метод, методы линеаризации
функционала (метод Маркуардта) и др.
Заметим,
что удачное начальное приближение точки
начала расчетов
![]() позволяет значительно сократить
трудоемкость расчетов, которые проводятся
до тех пор, пока изменения хотя бы одного
из параметров
,
ведут к уменьшению значения критерия
(8). Оптимальным признается такое значение
параметра
,
любые изменения которого ведут к
увеличению этого критерия.
позволяет значительно сократить
трудоемкость расчетов, которые проводятся
до тех пор, пока изменения хотя бы одного
из параметров
,
ведут к уменьшению значения критерия
(8). Оптимальным признается такое значение
параметра
,
любые изменения которого ведут к
увеличению этого критерия.
На практике приемлемую начальную точку процедуры расчетов можно определить, воспользовавшись линейным приближением функционала , имеющего следующий вид:
![]() (9)
(9)
где i – номер наблюдения
j – индекс независимого фактора
Заметим,
что для этой модели условное математическое
ожидание переменной
![]() определяется следующим образом:
определяется следующим образом:
![]() (10)
(10)
Из
выражений (9) и (10) также вытекает, что
ошибка модели принимает только два
значения
![]() с вероятностью
с вероятностью
![]() и
и
![]() с вероятностью
с вероятностью
![]() .
Это свидетельствует о «ненормальном»
характере закона распределения этой
ошибки. К другим «некорректностям»
модели (9) можно отнести гетероскедастичность
ошибки (поскольку она зависит от величины
факторов
.
Это свидетельствует о «ненормальном»
характере закона распределения этой
ошибки. К другим «некорректностям»
модели (9) можно отнести гетероскедастичность
ошибки (поскольку она зависит от величины
факторов
![]() и поэтому не обладает свойством
постоянства дисперсии). Кроме того,
прогнозные значения
и поэтому не обладает свойством
постоянства дисперсии). Кроме того,
прогнозные значения
![]() ,
которые по содержанию являются
вероятностями события
,
ничем не ограничены и могут находиться
за пределами отрезка [0;1].
,
которые по содержанию являются
вероятностями события
,
ничем не ограничены и могут находиться
за пределами отрезка [0;1].
Вместе с тем оценка параметров модели (9) на практике не представляет трудностей. Для этого могут быть использованы непосредственно метод наименьших квадратов или метод максимального правдоподобия. Найденные с помощью одного из этих методов оценки можно использовать как начальную точку итеративной процедуры поиска оптимума критерия (8).
Модификации модели бинарного выбора, различающиеся между собой в основном переменной Z, нашли достаточно широкое применение при оценке вероятностей дефолта заемщика кредитов. Например, согласно подходу, предложенному корпорацией КМФ, закон распределения вероятностей банкротства заемщика ставится в зависимость от показателя, определяемого как «расстояние до дефолта»:
![]() (11)
(11)
где P(D) – вероятность дефолта
В свою очередь это расстояние определяется как количество среднеквадратических отклонений, на которое должна снизиться стоимость активов компании-заемщика, прежде чем она объявит дефолт,
![]() (12)
(12)
где ν – стоимость компании, рассчитываемая как случайная величина
![]() -
ее математическое ожидание и
среднеквадратическое отклонение
соответственно
-
ее математическое ожидание и
среднеквадратическое отклонение
соответственно
Показатель DP определяет точку дефолта компании, т.е. такую стоимость ее активов, при которой компания объявляет дефолт:
![]() (13)
(13)
где STD – сумма краткосрочных обязательств компании
LTD – сумма ее долгосрочных обязательств
Функция F должна удовлетворять свойству (4), т.е. F(0)=1 (если дистанция до дефолта равна 0, то его вероятность равна 1, P(D)=1), F возрастает с ростом дистанции до дефолта в пределе до 1 и соответственно P(D) уменьшается в пределе до 0.
В литературе описано достаточно большое количество попыток выразить латентную переменную Z как функцию от факторов, характеризующих финансовую устойчивость предприятий (банка), и с использованием бинарной модели выбора оценить вероятность банкротства каждого из них.
