52. Коефіцієнт детермінації r2: формули для обчислення та сутність.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 5.2) і запишемо формулу для обчислення коефіцієнта детермінації:

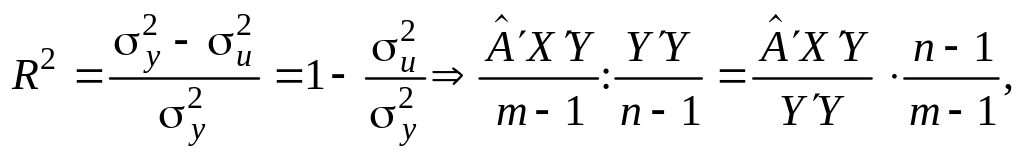(5.7)

або, не враховуючи ступенів свободи:

Оскільки у (5.7) задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (n – 1/m – 1) на число ступенів свободи (5.8), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

де R² — коефіцієнт детермінації з урахуванням числа ступенів свободи;

— коефіцієнт детермінації без урахування числа ступенів свободи.

Для функції з двома і більше незалежними змінними коефіцієнт детермінації може набувати значень на множині . Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної (Y) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Множинний коефіцієнт кореляції:

Він характеризує тісноту зв’язку усіх незалежних змінних із залежною.

Для множинного коефіцієнта кореляції з урахуваннням і без урахуванння числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

53. Теоретична та статистична лінійна множинна модель та їх запис у векторно-матричній формі.

На будь-який економічний показник У зазвичай впливає не один, а кілька факторів Х₁,Х₂,...,Х_т.

У подібних випадках маємо справу з множинною регресією, яку можна подати залежністю:

M(Y/X1, X2, …, Xm)=α(X1, X2, …, Xm)

Ця формула інформує про функціональну залежність умо­вного математичного сподівання залежної змінної У від т регресорів (незалежних, пояснювальних змінних) X = (Х,,Х2,...,Хт).

Задача оцінки статистичного взаємозв'язку між У та X = (Х1,Х2,..., Хт) формулюється аналогічно парній регресії.

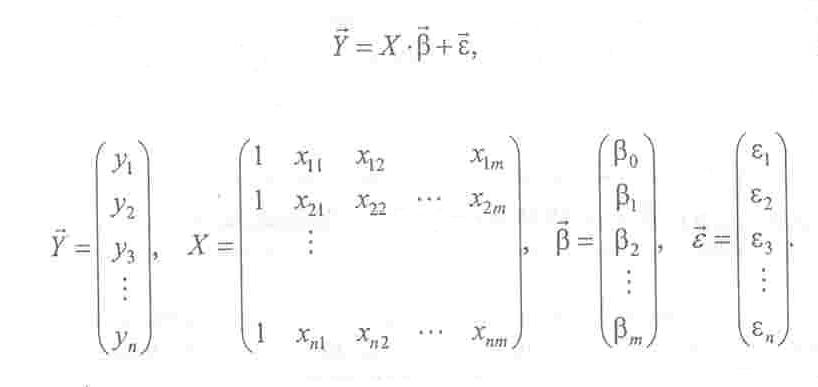
Розглянемо лінійну залежність ознаки У від т не­залежних змінних (регресорів) хі(і = 1,т). Лінійна теоретична модель може бути зображена в такому вигляді:

y1=β0+ β1x11+ β2x12+ β3x13+…+ βmx1m+ε1

…

yn=β0+ β1xn1+ β2xn2+ β3xn3+…+ βmxnm+εn

де (βi, i=1,m — теоретичні коефіцієнти регресії (часткові коефі­цієнти), які характеризують реакцію залежної змінної У на зміну регресора Xi, тобто, вони інформують про вплив на M{у / Х₁,Х₂,...,Х_ІП) пояснювальної змінної (регресора) Хi теоре­тичної моделі за умови, що решта регресорів цієї моделі залиша­ються сталими;

β 0 — вільний член, який визначає значення Y за умови, що всі регресори моделі дорівнюють нулю.

У векторно-матричній формі теоретичну модель можна подати так:

54. Умови Гаусса-Маркова для парної та множинної лінійної регресії.

Умови Гаусса—Маркова є такими:

1)Математичне сподівання випадкових відхилень є, має дорів­нювати нулеві:

Ця умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну У. Тоді для рівняння матимемо:

2) Дисперсія випадкових відхилень є,, має бути сталою вели­чиною:

3)Випадкові відхилення та , i не = j у мають бути незалеж­ними один від одного:

4) Випадкові відхилення мають бути незалежними від пояснювальних змінних Х: cov(εi, xi)=0, оскільки xi – не випадкова величина.

5) εi являє собою суму всіх можливих випадкових чинників, які впливають на значення залежної змінної y_t в моделі, при цьо­му дія кожного окремо взятого випадкового чинника на yi вважається несуттєвою.

6) Економетричні моделі мають бути лінійними відносно своїх параметрів.

Економетричні моделі, для яких виконуються умови (1)—(5), називають класичними моделями.

Економетричні моделі, для яких виконуються умови (1)—(6) називають класичними лінійними моделями.

Для множинної регресії умови Гаусса-Маркова аналогічні, як і для парної, а також включають таку умову між пояснювальними змінними моделі:

Тобто між векторами має бути відсутня лінійна (кореляційна) залежність, тобто |Хt*X|≠0. Коли |Хt*X|=0, такі моделі – мультиколінеарні.