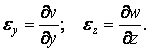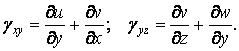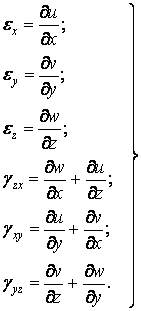- •1.1 Гіпотези й принципи теорії пружності
- •1.2 Напружений стан в точці тіла. Тензор напруг
- •1.2.1 Зовнішні сили й напруги
- •1.2.2 Диференціальні рівняння рівноваги
- •1.2.3 Визначення напруг на похилих площадках. Умови на поверхні
- •1.2.4 Головні напруги. Інваріанти напруженого стану
- •1.2.5 Тензор напруг. Найбільші дотичні напруження
- •1.3 Деформований стан у точці тіла. Тензор деформацій
- •1.3.1 Переміщення й деформації. Взаємозв'язок між ними
- •1.3.2 Об'ємна деформація
- •1.3.3 Рівняння нерозривності деформацій
- •1.3.4 Тензор деформацій. Головні деформації
- •1.4 Взаємозв'язок між тензорами напруг і деформацій. Узагальнений закон Гука
- •1.5 Робота пружних сил. Потенційна енергія деформацій
- •2.1 Повна система рівнянь теорії пружності
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •2.4 Типи граничних умов на поверхні тіла
- •2.5 Теорема одиничності. Методи рішення задачі теорії пружності
- •3.1 Плоска деформація і плоский напружений стан
- •3.2 Методи рішення плоскої задачі для прямокутних однозв'язних областей
- •3.3 Згинання консолі силою, прикладеною на кінці
- •3.4 Балка на двох опорах під дією рівномірно розподіленого навантаження
- •3.5 Трикутна підпірна стінка
- •3.6 Розрахунок балки-стінки
- •3.7 Обґрунтування принципу Сен-Венана
- •Розділ 4. ПлосКа задача теорії пружності у полярних координатах
- •4.1 Основні рівняння
- •4.2 Простий радіальний напружений стан
- •4.3 Клин, навантажений у вершині зосередженою силою
- •4.4 Стискання клина
- •4.5 Згинання клина
- •4.6 Дія зосередженої сили, прикладеної до границі напівплощини
- •4.7 Функція напружень для плоскої задачі в полярних координатах
- •4.8 Осесимметричні задачі. Рішення в переміщеннях
- •4.9 Розрахунок труби з товстими стінками (задача Ламе)
- •4.10 Рішення осесимметричної задачі за допомогою функції напружень
- •4.11 Чистий вигин криволінійного бруса. Задача Головіна
- •4.12 Поняття про розрахунок циліндричних котків
- •6.13 Поняття про дію зосередженої сили на пружний півпростір
- •5.1 Основні поняття й гіпотези
- •5.2 Переміщення і деформації в пластинці
- •5.3 Напруження в пластинці
- •5.4 Зусилля в пластинці
- •5.5 Вираження напружень через зусилля
- •5.6 Диференційне рівняння зігнутої серединної поверхні пластинки
- •5.7 Умови на контурі пластинки
- •5.8 Прямокутна пластинка. Рішення Нав’є
- •5.9 Прямокутна пластинка. Розв’язок Леві
- •5.10 Поняття про розрахунок прямокутної пластинки й нескінченної смуги на пружній основі
- •5.11 Основні рівняння вигину круглої пластинки
- •5.12 Найпростіші осесиметричні задачі вигину круглої пластинки
- •5.13 Поняття про розрахунок гнучких пластинок
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.1 Сутність варіаційних методів розв’язання
- •6.2 Метод Рітца-Тимошенко
- •6.3 Метод Бубнова-Гальоркіна
- •6.4 Метод Власова
- •6.5 Потенційна енергія при вигині пластинки
- •6.6 Приклад розв’язання задачі методом Рітца-Тимошенко
- •6.7 Приклад розв’язання задачі методом Бубнова-Гальоркіна
1.3 Деформований стан у точці тіла. Тензор деформацій
1.3.1 Переміщення й деформації. Взаємозв'язок між ними
Для визначення деформації пружного тіла зрівняємо положення точок тіла до й після прикладення навантаження.
Розглянемо точку
ненавантаженого тіла і її нове положення
![]() після прикладення навантаження. Вектор
після прикладення навантаження. Вектор
![]() називається вектором
переміщення точки
(рис.1.4).
називається вектором
переміщення точки
(рис.1.4).
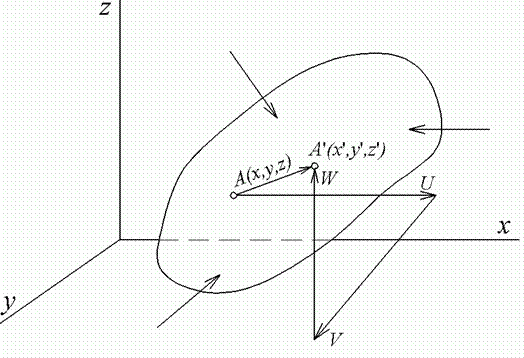
Рис.1.4. Вектор переміщення точки
Можливі два види переміщень: переміщення всього тіла як єдиного цілого без деформування - такі переміщення вивчає теоретична механіка як переміщення абсолютно твердого тіла, і переміщення, пов'язане з деформацією тіла - такі переміщення вивчає теорія пружності.
Позначимо проекції вектора
переміщення точки
на координатні осі
![]() через
через
![]() відповідно. Вони рівні різниці відповідних
координат точок
і
:
відповідно. Вони рівні різниці відповідних
координат точок
і
:
![]()
і є функціями координат:
![]()
Деформування тіла викликане
різницею в переміщеннях різних його
точок. Нескінченно малий паралелепіпед
з ребрами
![]() вирізаний із пружного тіла біля довільної
точки
,
внаслідок різних переміщень його точок
деформується таким чином, що змінюється
довжина його ребер і спотворюються
спочатку прямі кути між гранями.
вирізаний із пружного тіла біля довільної
точки
,
внаслідок різних переміщень його точок
деформується таким чином, що змінюється
довжина його ребер і спотворюються
спочатку прямі кути між гранями.
На рис.1.5 показані два ребра
цього паралелепіпеда:
![]() і
і
![]() довжина ребра
довжина ребра
![]() дорівнює
дорівнює
![]() а ребра
а ребра
![]() —
—
![]()
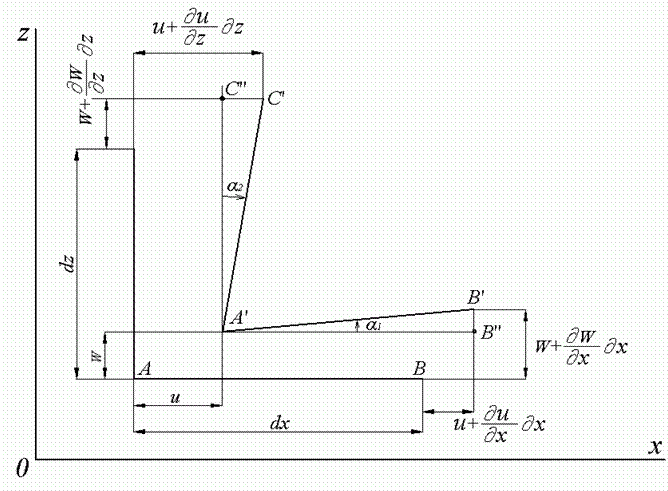
Рис.1.5. Лінійні й кутові деформації
Після деформації точки
![]() приймають положення
приймають положення
![]() При цьому точка
одержить переміщення, складові якого
в площині креслення рівні
При цьому точка
одержить переміщення, складові якого
в площині креслення рівні
![]() й
й
![]() Точка
Точка
![]() віддалена від точки
на нескінченно малій відстані
одержить переміщення, складові якого
будуть відрізнятися від складових
переміщення точки
на нескінченно малу величину за рахунок
зміни координати
віддалена від точки
на нескінченно малій відстані
одержить переміщення, складові якого
будуть відрізнятися від складових
переміщення точки
на нескінченно малу величину за рахунок
зміни координати
![]()
![]()
Складові переміщення точки
![]() будуть відрізнятися від складових
переміщення точки
на нескінченно малу величину за рахунок
зміни координати
будуть відрізнятися від складових
переміщення точки
на нескінченно малу величину за рахунок
зміни координати
![]()
![]()
Довжина проекції ребра на вісь після деформації:
|
(1.31) |
Проекція абсолютного подовження ребра на вісь
![]()
Відносне подовження уздовж осі
|
(1.32) |
називається лінійною деформацією по напрямку осі .
Аналогічно визначаються лінійні деформації по напрямках осей і
|
(1.33) |
Розглянемо зміну кутів між
ребрами паралелепіпеда (рис.1.5). Тангенс
кута повороту ребра
в площині
![]()
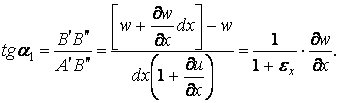
Внаслідок малості деформацій
![]() а лінійною деформацією
а лінійною деформацією
![]() можна зневажити через її малість у
порівнянні з одиницею, і тоді
можна зневажити через її малість у
порівнянні з одиницею, і тоді
![]()
Аналогічним чином можна визначити кут повороту ребра в тій же площині:
![]()
Перекручування прямого кута
![]() називається кутовою деформацією й
визначається як сума кутів повороту
ребер
і
:
називається кутовою деформацією й
визначається як сума кутів повороту
ребер
і
:
|
(1.34) |
У такий же спосіб визначаються кутові деформації у двох інших координатних площинах:
|
(1.35) |
Формули (1.32)-(1.35) дають шість основних залежностей для лінійних і кутових деформацій від складових переміщення. Ці залежності називаються рівняннями Коші:
|
(1.36) |
В межі, коли довжини ребер
паралелепіпеда прямують до нуля,
співвідношення Коші визначають лінійні
й кутові деформації в околиці точки
![]()
Позитивним лінійним деформаціям відповідають подовження, а негативним — укорочення. Кут зсуву вважається позитивним при зменшенні кута між позитивними напрямками відповідних координатних осей і негативним — у противному випадку.