Доведення

як ймовірність неможливої події .

як ймовірність достовірної події .

4. Ймовірність потрапляння випадкової величини на проміжок дорівнює приросту її функції розподілу на цьому інтервалі, тобто

. (1.19)

Формула (1.19) випливає безпосередньо з формули (1.18).

5. Неперервні випадкові величини. Щільність ймовірності

Враховуючи розглянуте поняття функції розподілу, неперервною випадковою величиною називають випадкову величину, функція розподілу якої неперервна та диференційовна в усіх точках. Має місце теорема.

Теорема 1.1 Ймовірність будь-якого окремо взятого значення неперервної випадкової величини дорівнює нулю.

Доведення

Покажемо, що для довільного значення випадкової величини ймовірність . Подамо у вигляді

.

Застосувавши властивість (4) функції розподілу і враховуючи неперервність , одержимо

.

До цих пір ми розглядали випробування, які зводились до схеми випадків, і нульову ймовірність мали лише неможливі події. З наведеної теореми випливає,що нульову ймовірність можуть мати і можливі події.

Наслідок. Якщо – неперервна випадкова величина, то ймовірність потрапляння випадкової величини на проміжок не залежить від того, є цей проміжок відкритим чи закритим, тобто

.

Дійсно,

.

Аналогічно доводяться інші рівності.

Подання неперервної випадкової величини за допомогою функції розподілу не є єдиним. Введемо поняття щільності ймовірності неперервної випадкової величини.

Щільністю ймовірності (closeness of probability) (або просто щільністю) неперервної випадкової величини називається похідна її функції розподілу

. (1.20)

Про випадкову величину кажуть, що вона розподілена із щільністю на певному проміжку осі абсцис. Функція є однією з форм закону розподілу, але існує вона лише для неперервних випадкових величин. Щільність ймовірності іноді називають диференціальним законом розподілу. Графік щільності ймовірності називають кривою розподілу.

Приклад 1.11 Знайти щільність розподілу ймовірності випадкової величини задану функцією розподілу

.

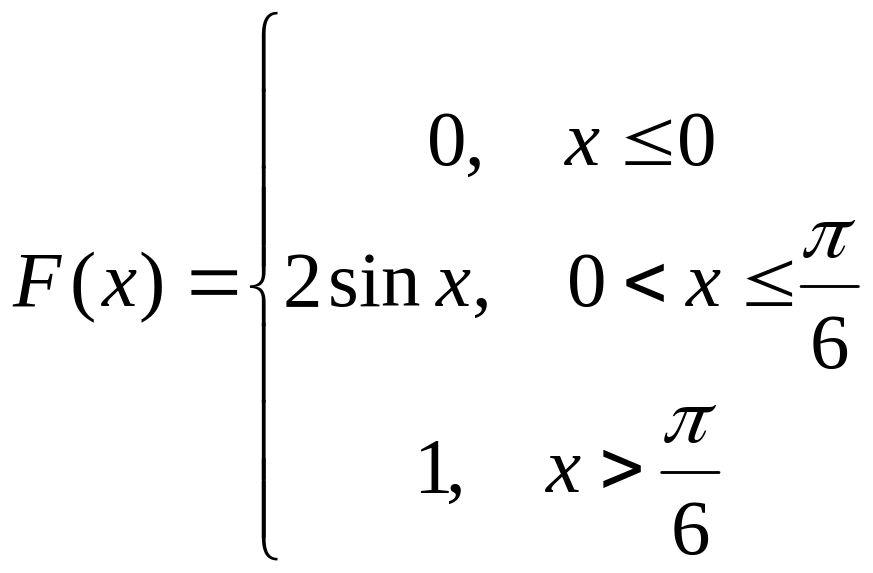Розв’язування

За формулою (1.20) маємо

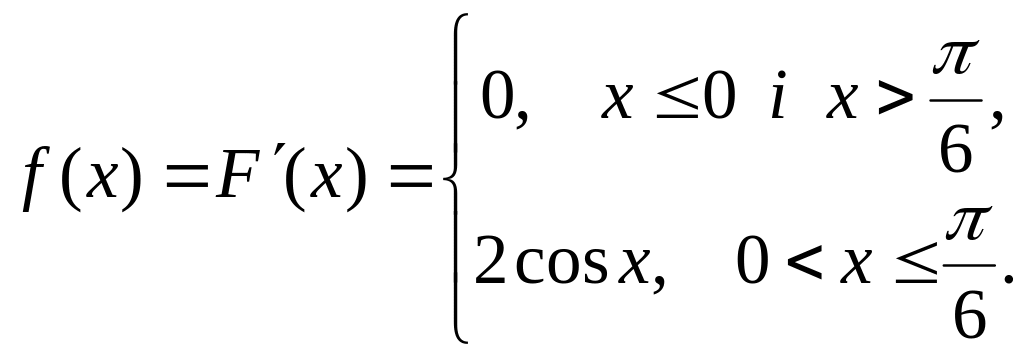
Розглянемо загальні властивості щільності ймовірності неперервної випадкової величину.

1. Щільність ймовірності – невід’ємна функція, тобто

.

Дійсно, оскільки функція розподілу неспадна, то .

2. Ймовірність потрапляння неперервної випадкової величини на проміжок дорівнює визначеному інтегралу від її щільності ймовірності в межах від до , тобто

. (1.21)

Доведення

За (4) властивістю функції розподілу маємо

.

Оскільки є первісною для щільності ймовірності, то за формулою Ньютона – Лейбніца приріст первісної на відрізку є визначений інтеграл , тобто

.

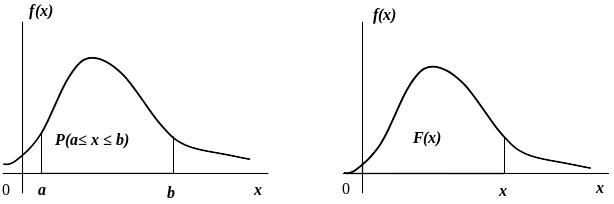З геометричної точки зору одержана ймовірність дорівнює площі криволінійної трапеції, обмеженої кривою розподілу, віссю та прямими та .

Рисунок 1.6

3. Функція розподілу неперервної випадкової величини знаходиться через щільність ймовірності за формулою:

. (1.22)

Формула (1.22) може бути одержана з (1.21) при , якщо замінити верхню межу на змінну межу .

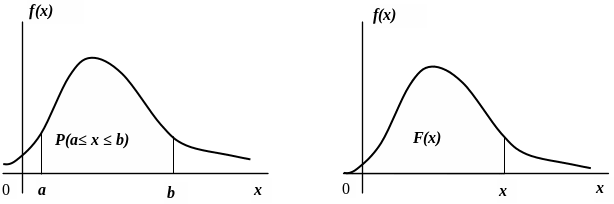З геометричної точки зору функція розподілу дорівнює площі фігури, обмеженої зверху кривою розподілу та розташованої лівіше точки (рис. 1.7).

Рисунок 1.7

4. Невласний інтеграл у нескінченних межах від щільності ймовірності неперервної випадкової величини дорівнює одиниці:

. (1.23)

Дійсно, за формулою (1.22): та при .

Поняття математичного сподівання та дисперсії, розглянуті для дискретної випадкової величини, можна розповсюдити на неперервні випадкові величини. Для одержання відповідних формул достатньо у формулах (1.3) та (1.11) для дискретної випадкової величини замінити знак підсумовування знаком інтеграла із нескінченними межами , можливі значення – неперервною змінною , а ймовірність – елементом ймовірності .

Зауваження. Під елементом ймовірності розуміють ймовірність потрапляння випадкової величини на проміжок .

В результаті одержуємо такі формули для математичного сподівання та дисперсії неперервної випадкової величини :

(1.24)

(якщо інтеграл абсолютно збіжний) та

(1.25)

(якщо інтеграл збіжний).

Усі властивості математичного сподівання та дисперсії, розглянуті для дискретних величин, справедливі і для неперервних. Зокрема, на практиці при обчисленні дисперсії використовують формулу:

. (1.26)

Приклад 1.12 Дано функцію:

.

Знайти: а) значення сталої , при якому дана функція буде щільністю ймовірності деякої випадкової величини ; б) вираз для функції розподілу ; в) обчислити ймовірність того, що випадкова величина набуде значення з відрізку ; г) математичне сподівання та дисперсію випадкової величини .