Розв’язування

Знайдемо загальну середню за формулою (3.7):

(грн.)

За формулою (3.13) маємо:

;

За формулою (3.15) коефіцієнт варіації обчислюється так

(%).

Приклад 3.4 Обчислити коефіцієнти асиметрії та ексцес розподілу кравчинь за виробітком за даними табл. 3.2

Розв’язування

З прикладу 3.2 відомо, що , тому

=

;

.

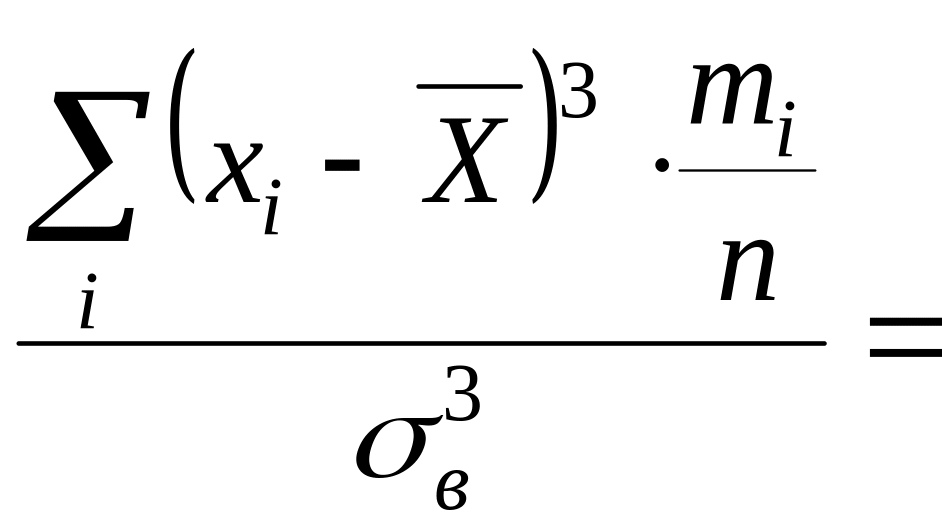
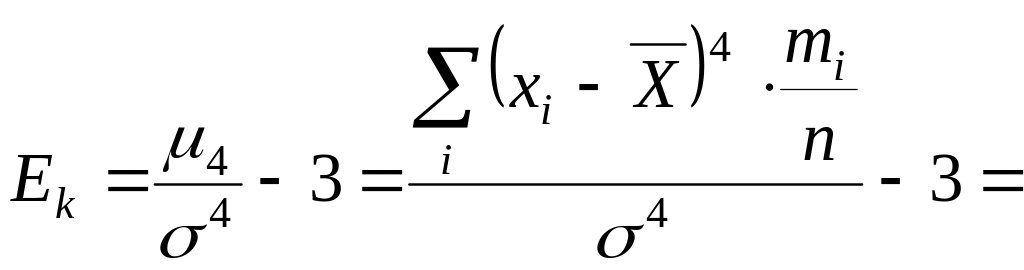
Приклад 3.5 Задана генеральна сукупність з 20 елементів. Виконати такі вправи:

1. побудувати статистичний розподіл вибірки та його емпіричну функцію розподілу;

2. обчислити числові характеристики вибірки: середнє, дисперсію і середнє квадратичне відхилення та зробити з їх допомогою висновок про генеральну сукупність;

3. побудувати полігон частот і відносних частот та гістограму, розбивши інтервал на 4 рівних підінтервали;

4. знайти моду, медіану, розмах і коефіцієнт варіації.

Розв’язування

У нашому випадку задано таку генеральну сукупність: 15, 19, 13, 12, 9, 14, 15, 19, 12, 17, 13, 9, 15, 12, 15, 14, 18, 16, 15, 12.

1) Статистичний розподіл вибірки:

	9	12	13	14	15	16	17	18	19
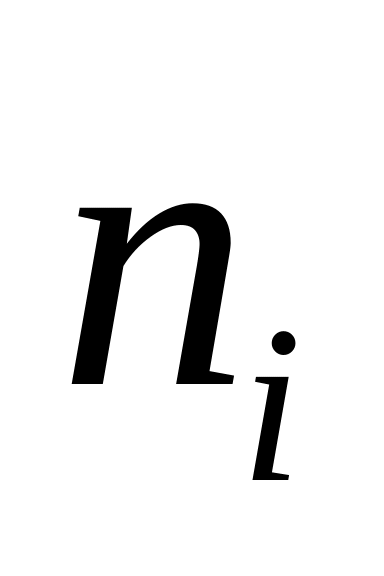
	2	4	2	2	5	1	1	1	2

; ; ; ; ; ; ; ; ;

Емпірична функція розподілу : , де - число варіант, менших від ; - об’єм вибірки; .

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

, ;

Або

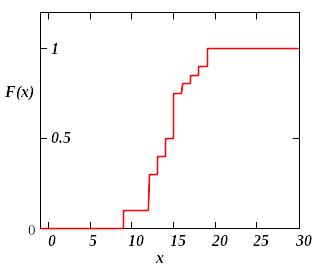
Рисунок 3.3

Графік емпіричної функції розподілу подано на рис. 3.3

2) Числові характеристики вибірки.

Вибіркове середнє :

(незміщена оцінка математичного сподівання генеральної сукупності):

Вибіркова дисперсія (зміщена оцінка дисперсії генеральної сукупності):

.

.

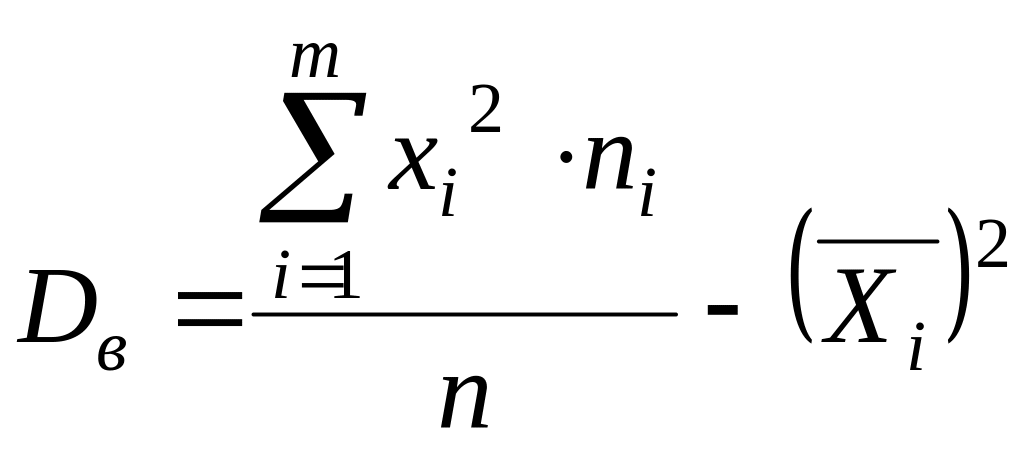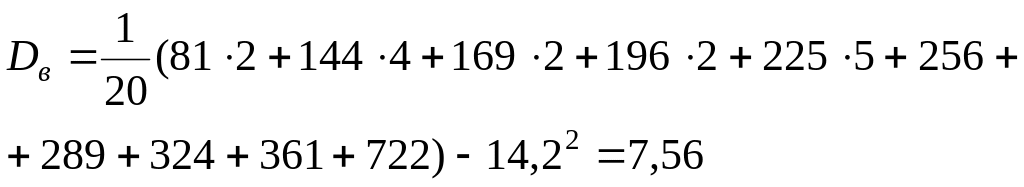
Середнє квадратичне відхилення: , характеризує середню величину розсіювання значень навколо середньої вибіркової .

3) ; ; ; ; ; ;

; ; .

Розбиваємо інтервал на 4 інтервали:

Інтервал	[9;11,5]	[11,5;14]	[14;16,5]	[16,5;19]
Сума частот	2	6	8	4

Побудуємо гістограму(східчасту діаграму) частот (рис. 3.4).

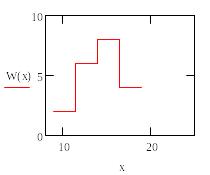
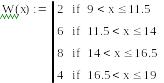
Рисунок 3.4

4) Модою є варіанта, якій відповідає найбільша частота. В нашому випадку .

Медіаною називається число, яке ділить варіаційний ряд на дві частини, рівні по числу варіант, тому .

Розмах варіації ( ) – це різниця між найбільшою та найменшою варіантами ; .

Коефіцієнт варіації: ;

.

Вправи

У вправах 3.1-3.3 задано розподіл ознаки (випадкової величини ), одержаної в результаті спостережень. Необхідно: 1) побудувати полігон (гістограму) та емпіричну функцію розподілу ; 2) знайти: а) середню арифметичну; б) медіану та моду; в) дисперсію, середнє квадратичне відхилення та коефіцієнт варіації; г) початкові та центральні моменти -го порядку ; коефіцієнт асиметрії та ексцес.

3.1 – кількість угод агентства нерухомості за квартал; (інвесторів).

	0	1	2	3	4	5	6	7	8	9	10
	201	95	71	32	23	5	5	2	3	1	1

3.2 – місячний дохід жителя м. Вінниці (в грн.); (жителів)

	Менше 650	650-1150	1150-1650	1650-2150	2150-2650	Понад 2650
	58	96	239	328	147	132

3.3 – надій корів на молочній фермі за лактаційний період (в ц.); (корів).

	4-6	6-8	8-10	10-12	12-14	14-16	16-18	18-20	20-22	22-24	24-26
	1	3	6	11	15	20	14	12	10	6	2