2.8. Методика обучения учащихся решению задач в теме «Признаки равенства треугольников»

В заключение главы рассмотрим в качестве примера, как в конкретной теме, на одних и тех же задачах может осуществлять­ся обучение учащихся решению и типовых задач, и общим умени­ям по решению задач.

Признаки равенства треугольников мощный аппарат для решения задач. Поэтому проблема овладения учащимися умени­ями по решению задач этого вида стоит очень остро. «Признаки равенства треугольников» - тема начала систематического кур­са геометрии, и поэтому многие трудности курса, такие как от­сутствие умений по решению геометрических задач, по решению задач вообще, проявляют себя в полной мере в этой теме. Реше­ние задач с помощью признаков равенства треугольников требу­ет от учащихся также определенных частных умений, относящих­ся только к этой теме.

Тема «Признаки равенства треугольников» неизменно прико­вывает внимание учителей и методистов, пытающихся снять труд­ности темы с помощью расширяющегося методического аппарата.

Анализ решения задач по теме позволяет классифицировать их по уровню сложности следующим образом:

1. Задачи, в которых необходимо доказать равенство некото­рых двух треугольников.

2. Задачи, в которых необходимо установить равенство двух отрезков или двух углов, опираясь на доказательство равенства двух треугольников. К задачам этого уровня сложности относят­ся также такие, в которых требуется найти численное значение длины отрезка или меры угла, опираясь на доказанное равенство отрезков и углов, а также установить факт, сводимый к равен­ству отрезков или углов (наличие биссектрисы, середины отрез­ка, равнобедренного треугольника и т. д.).

3. Задачи, в которых приходится осуществлять переход от од­ной пары равных треугольников к другой.

Приведенная классификация задач по уровню сложности оп­ределяет последовательность в подборе системы задач на призна­ки равенства треугольников. Однако она лишь в очень ограни­ченной мере вскрывает операционный состав действия решения таких задач - соответствующего частного умения.

Чтобы помочь учащимся овладеть сложным умением решать задачи с помощью признаков равенства треугольников, необхо­димо проанализировать, из каких операций состоит это умение. Оно складывается как из операций общего плана, имеющих мес­то при решении задач в различных темах, так и из специфических, имеющих место при решении задач только в данной теме.

Согласно теории деятельности, каждая операция, которая при­сутствует в действии, предварительно сама должна быть развер­нутым действием с наличием соответствующей цели. Это действие необходимо специально формировать. Поэтому далее, одновре­менно с выделением операций, из которых состоит действие ре­шения задач с помощью равенства треугольников, предлагаются примеры заданий по формированию этих операций, а учитель смо­жет найти им место в процессе обучения, а также при необходимо­сти составить подобные. Часть заданий может быть выполнена заблаговременно, до изучения признаков, а часть - войдет в сис­тему задач, решаемых в теме. Такими операциями являются сле­дующие.

1. Выделение в задаче условия и заключения. Подсчет количе­ства данных и требований. Последняя рекомендация особенно эффективна в начале процесса обучения решению задач. Если в курсе арифметики такая работа не проводилась, то в начале кур­са геометрии она необходима для самоконтроля, для выполнения последующей операции - получения следствий. При этом следует делать упор не на числовых данных задачи, а на величинах, входя­щих в текст задачи и на соотношениях между ними, на количестве рассматриваемых в задаче ситуаций. Тем самым организуется про­никновение в структуру задачи и удерживается в памяти условие задачи, без чего невозможна дальнейшая актуализация знаний.

ПРИМЕР. Доказать, что в равных треугольниках медианы, проведенные из соответствующих вершин, равны. Перечислите все данные задачи и сделайте чертеж (рис. 19).

А

А₁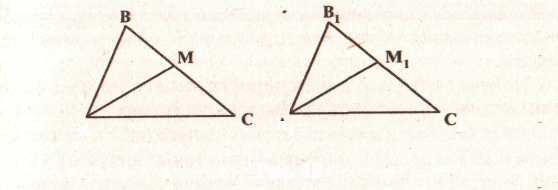

Рис. 19

В результате анализа условия задачи получается запись:

Дано: 1)⊿ВС=⊿А₁В₁С₁; 2) ЛМ-медиана; 3)А₁М₁ -медиана.

Доказать: АМ=А₁М_[.

Такой работе над условием задачи, к сожалению, специально­го внимания не уделяется. Предполагается, что ученик овладева­ет ею в процессе выполнения более сложной деятельности реше­ния задач. А это действие требует специальной отработки, кор­ректировки и оценивания.

2. Перевод в тексте задачи обычной речи на математический язык геометрической модели (чертежа), на язык понятий и отно­шений. Перевод может иметь место как в данных, так и в требо­вании задачи.

При этом следует иметь в виду, что различные обороты речк, имеющие одну и ту же математическую суть, поначалу восприни­маются учащимися как имеющие разный смысл.

С учащимися необходимо разобрать ситуации типа: точка О делит отрезок АВ пополам, точка О - середина отрезка, АО -половина АВ, АВ больше OB (OA) в 2 раза и выяснить, что смысл их - один. Необходимо также разобрать ситуацию: два отрезка в точке пересечения делятся пополам, точка одинаково удалена от концов отрезка, прямая проходит через середину отрезка и т. д. При этом задания могут быть взаимно-обратного характера: изоб­разить ситуацию на чертеже или словами (в различной форме) описать ситуацию, изображенную на чертеже.

3. Замена математических понятий отношениями, содержащи­мися в определении понятия.

Задание для учащихся: объясните, что означает тот факт, что AD - медиана ⊿АВС, ВК - биссектриса ⊿АВС, что ⊿АВС = = ⊿А₁В₁ С,. Операция замены понятий отношениями, свойствами, содержащимися в определении, имеет место на стыке двух этапов процесса решения задачи: это еще анализ условия и уже поиск решения.

4. Получение ближайших следствий из условия задачи. Таки­ми следствиями могут быть предыдущая операция - замена тер­минов отношениями; приведение свойств понятий, содержащих­ся и не содержащихся в определении, а также получение след­ствий сразу из нескольких составных частей условия. Операция получения следствий может быть представлена различными граф-схемами (см. рис. 20):

Точки нижнего ряда изображают отдельные составляющие ус­ловия, а точки верхнего ряда - полученные из них следствия. Тог­да первая схема моделирует наличие одного вывода из одного ус­ловия (AD - биссектриса угла; следовательно, ∠BAD = ∠CAD), вторая и третья схемы - получение нескольких выводов из одно­го условия (⊿ЛБС - равнобедренный, следрвательно, АВ = АС, ∠B=∠C). На четвертой и пятой схемах представлены сопоставление данных и получение вывода из них (∠1= ∠A,∠3 = ∠A₁,

∠A -∠A₁ следовательно, ∠1 =∠3).

Упражнения на получение граф-схем - материализованной формы операции получения следствий полезно выполнять каждо­му учащемуся.

Полезно на граф-схемах показать и полное решение задачи, что позволит учащимся проникнуть в процесс решения задачи и выйти из тупика. На уроке для построения граф-схем возможно привлечение магнитной доски и специально заготовленных лис­точков с записями различных отношений. Например, учитель при­крепляет к магнитной доске маленький плакатик: ⊿АВС- равно­бедренный и просит среди имеющихся плакатиков выбрать те, которые являются следствиями имеющегося факта. Получается граф-схема:

ПРИМЕРЫ. Получите различные следствия из следующих условий:

1. В равнобедренном треугольнике с основанием АС боковая сторона АВ равна 2 см.

2. ААВС- равнобедренный с основанием^С, AD =ЕС (см. рис. 21):

Рис. 22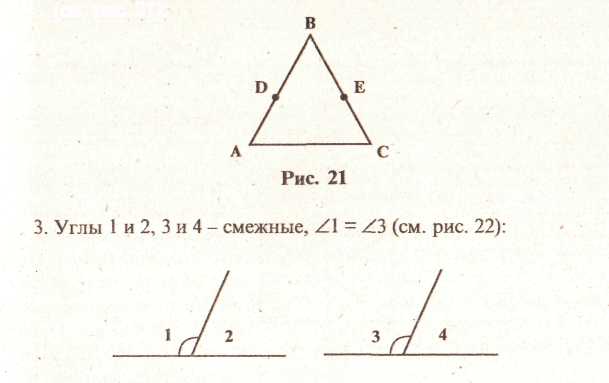

4. В равнобедренном треугольнике отмечены середины всех сто­рон.

Как можно видеть, задания на получение следствий нацелива­ют учащихся на самостоятельное составление задач. Задания могут иметь разное продолжение. Они обучают целегюлаганию -действию, без которого трудно обойтись при решении сложных практических задач.

Все рассмотренные выше операции действия решения задач с помощью признаков равенства треугольников специфическими для этого вида задач не являются. Они имеют место при решении содержащимися в определении, имеет место на стыке двух этапов процесса решения задачи: это еще анализ условия и уже поиск решения.

4. Получение ближайших следствий из условия задачи. Таки­ми следствиями могут быть предыдущая операция - замена тер­минов отношениями; приведение свойств понятий, содержащих­ся и не содержащихся в определении, а также получение след­ствий сразу из нескольких составных частей условия. Операция получения следствий может быть представлена различными граф-схемами (см. рис. 20):

Методика преподавания математики в средней школе I

любой математической задачи. Остальные операции - специфи­ческие, они имеют место только в данной теме.

5. Поиск равных элементов в треугольниках, если существует взаимопроникновение элементов. Эта операция требует рассмот­рения одного и того же элемента - стороны, угла - под разными углами зрения, как принадлежащих разным треугольникам. Это самый сложный вид сравнения - сравнение с самим собой. Приве­дем примеры соответствующих упражнений: 1. Найдите равные элементы в треугольниках, представленных

на рис. 23.

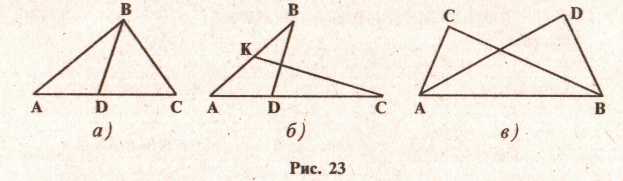
2. Укажите, стороной каких треугольников является отрезок ОВ; углом каких треугольников является ZA (рис. 24).

B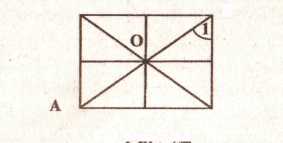

Рис. 24

6

K

. Нахождение соответствующих элементов в треугольниках, равенство которых установлено. Приведем примеры. 1. Укажите все пары соответственно равных элементов в дан­ных треугольниках (рис. 25). Объясните ответ.

[Лекция 2. Методика обучения учащихся решению...

2. Укажите соответственно равные элементы равных треуголь­ников (рис. 26). Объясните ответ. С

3

C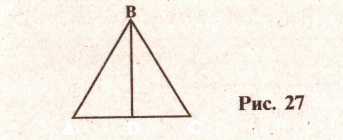

. Найти соответственно равные элементы в равных треуголь­никах (рис. 27). Объясните ответ.

7. Выбор признака, выделение трех пар соответственно рав­ных элементов, установление равенства треугольников подведе­нием под выбранный признак.

Может показаться, что поскольку указанная операция имеет место при решении любой задачи, то специальных упражнений на нее не требуется. Однако смысл прелагаемых заданий состоит в том, что ученику сразу предлагается несколько ситуаций, упро­щенных наличием готовых чертежей, которые необходимо срав­нить между собой, осуществить выбор признака, каждый раз най­дя три пары соответственно равных элементов.

ПРИМЕР. Укажите, каким признаком вы будете пользовать­ся для доказательства равенства каждой пары треугольников (рис. 28, а-r) и почему.

Методика преподавания математики в средней школе |

8. Поиск, выделение пары равных треугольников, которым принадлежат элементы, равенство которых требуется доказать.

ПРИМЕРЫ. Укажите, равенство каких треугольников надо доказать для решения задач:

1. Доказать равенство двух биссектрис равнобедренного тре­угольника, проведенных из вершин основания.

2. Доказать, что середины сторон равнобедренного треугольни­ка являются вершинами равнобедренного треугольника.

3. Треугольник ABC- равнобедренный, BD-BE, доказать ра­венство углов САЕ и DC А (рис. 29).

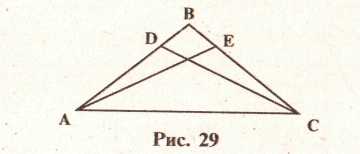
9. В теме «Признаки равенства треугольников» может быть положено начало выделению «зон поиска» различных ситуаций, а именно равенства отрезков и углов. «Зона поиска» - это набор достаточных условий для существования объекта, отношения. Акцентирование внимания на этих зонах помогает в преобразо­ваниях требования задачи, в продвижении решения задачи с кон­ца. Требование, цель, преобразуются так, чтобы более соответ­ствовать данным задачи. Например, «зоной поиска» равных от­резков могут быть условия: быть соответственными сторонами в равных треугольниках, быть боковыми сторонами равнобедрен­ного треугольника, иметь равную длину, совпадать при наложе­нии и многое другое.

' Отдельные методисты советуют вести учет «зон поиска» рав­ных отрезков и углов на протяжении первых двух лет обучения геометрии для осуществления систематизации изучаемого геомет­рического материала по определенной линии.

Выделение перечисленных операций способствует осознанию учителем тех трудностей, которые испытывают учащиеся при ре­шении задач на признаки равенства треугольников, помогает бо­лее тщательно отрабатывать методику обучения учащихся решению задач в теме, управлять мыслительной деятельностью уча­щихся.

Перечисленные операции представляют собой отдельные шаги сложного действия по решению задач с помощью признаков ра­венства треугольников. Эти шаги могут быть объединены в пред­писание и предъявлены учащимся в явном виде. Тогда предписа­ние может выглядеть следующим образом:

1. Выдели в задаче данные и требование.

2. Замени понятия их определениями. При необходимости пе­реведи фразы с обычного языка на математический.

3. Если требуется доказать равенство треугольников, то:

а) укажи, равенство каких элементов этих треугольников из­вестно из условия;

б) найди, какого условия не хватает, чтобы воспользоваться тем или иным признаком;

в) посмотри, нельзя ли получить недостающее равенство как следствие какого-либо условия;

г) если попытка использования выбранного признака не уда­лась, повтори шаги (б-г), используя другой признак;

д) перечисли три пары соответственно равных элементов двух выбранных треугольников для получения вывода о равен­стве треугольников.

4. Если требуется доказать равенство двух отрезков или двух углов, то попытайся выделить треугольники, равенство которых можно доказать и которым принадлежат упомянутые элементы, для чего проведи операцию (3). Сделай соответствующие выводы.

5. Если задачу решить не удалось, возвращайся к началу пред­писания.

Приведенное предписание является предписанием полуалго­ритмического типа, т. к. порядок выполнения операций при ре­шении конкретной задачи может быть изменен, отдельные опера­ции могут отсутствовать и вообще предписание может не привес­ти к получению желаемого результата.

Полученное предписание является итогом большой предвари­тельной работы с учащимися, в которой отрабатываются по отдельности шаги этого предписания.

Приведенное предписание имеет сравнительно сложную струк­туру. Работа по его использованию при решении задачи может быть упрощена, если отдельные операции предписания предъявить не как цельный алгоритм, а как некоторый набор отдельных рекомен­даций, правил, которых целесообразно придерживаться при реше­нии задач на признаки равенства треугольников. Эти рекоменда­ции могут быть выделены учащимися с помощью учителя на этапе исследования полученного решения в отдельных задачах.

Отметим также, что каждый признак равенства треугольников должен быть вначале закреплен сам по себе и лишь потом встроен в систему признаков с помощью специальных систем упражнений. Если сравнить системы упражнений по алгебре и по геометрии, то можно увидеть, что в курсе алгебры каждое правило закрепляется большим количеством однотипных примеров (от 20 до 100), в кур­се геометрии на закрепление первого признака равенства треуголь­ников в учебных пособиях приводится 4—5 задач. А отдельные со­ставляющие умения по решениюзадач с помощью признаков ра­венства треугольников вообще никак не отрабатываются.

Приведем систему задач на закрепление первого признака равенства треугольников. Эта система отличается от имеющихся в учебных пособиях не только количеством и порядком, но и на­личием простейших задач, необходимых для обучения учащихся в начале систематического курса геометрии. Вышеприведенные упражнения также должны занять свое место в предлагаемой сис­теме. Часть приведенных задач может быть решена на этапе пер­вичного закрепления, а часть - при совместном решении задач на различные признаки, где имеет место выбор признака. При необ­ходимости можно легко составить аналогичные системы задач по остальным признакам.

1. Доказать равенство треугольников (рис. 30).

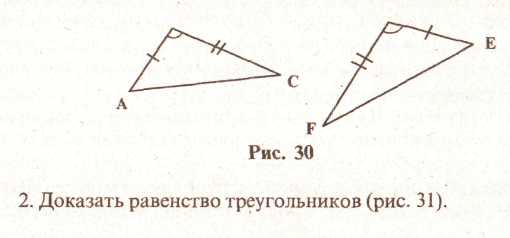
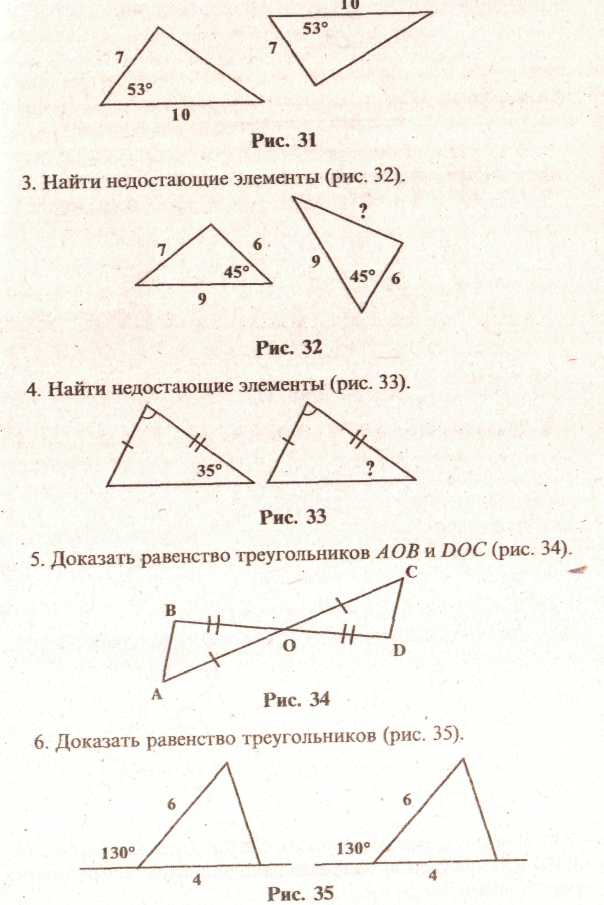
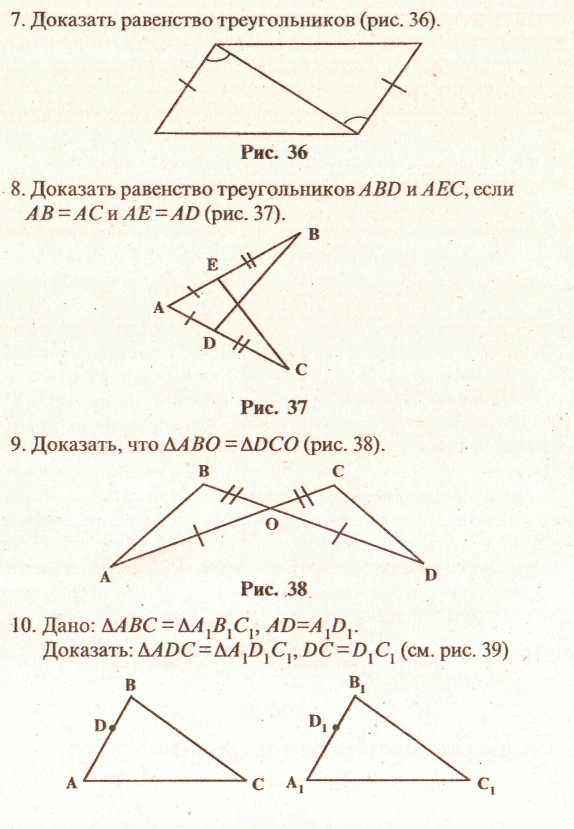
Рис. 39

11. В равных треугольниках ABC и A_lB_lC_l проведены медиа­ны AD и А₁D₁ из соответствующих вершин. Доказать равенство треугольников ADC и A _lD₁ С₁.

12. Треугольник ABC- равнобедренный. Доказать, что бис­сектриса угла при вершине является его медианой и высотой.

13. Доказать, что в равнобедренном треугольнике углы при основании равны.

14. Доказать, что середины сторон равнобедренного треуголь­ника являются вершинами равнобедренного треугольника.

15. Медианы, биссектрисы, высоты, проведенные из вершин основания равнобедренного треугольника, равны между собой.

16. Доказать: АВ -ВС (см. рис. 40).

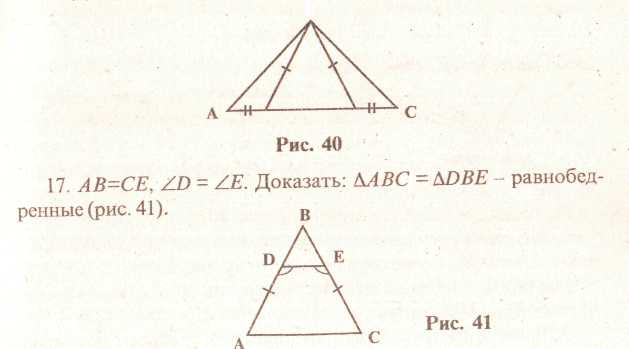
В завершении раздела рассмотрим в качестве примера реше­ние задачи с помощью предписания и с использованием граф-схе­мы, что позволяет продемонстрировать учащимся в материализо­ванной форме процесс поиска решения конкретной задачи.

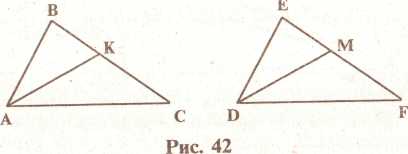
ЗАДАЧА. Доказать, что в равных треугольниках биссектри­сы соответствующих углов равны (рис. 42).

Методика преподавания математики в средней школе I

1. Выделим условие и заключение в виде основания и верши­ны граф-схемы:

3. Выделим треугольники, сторонами которых являются от­резки АК и DM, равенство которых требуется доказать. Возмож­ны два варианта. Сделаем попытку доказать равенство треуголь­ников АКС и DMT.

4. Выполним третий шаг предписания, докажем равенство выделенных треугольников. На граф-схеме этот шаг изобразится следующим образом:

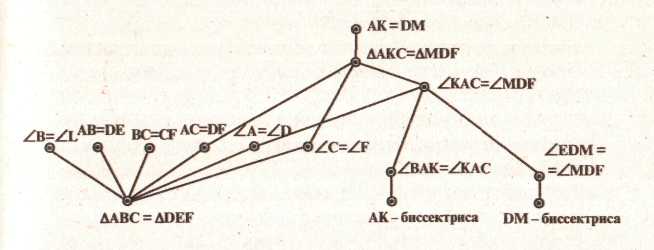I Лекция 2. Методика обучения учащихся решению...

5. Сделаем выводы относительно равенства соответствующих сторон AK и DM в равных треугольниках:

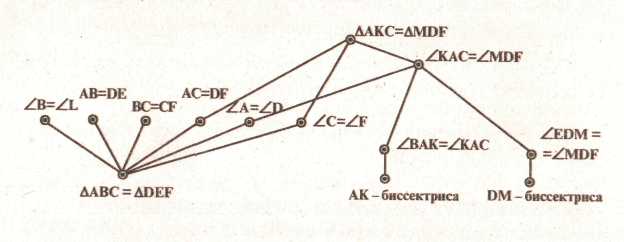
Нет необходимости решать большое количество задач с помо­щью граф-схем. Но решением в таком виде ряда задач полезно продемонстрировать учащимся в материализованной форме вы­полнение как отдельных операций: выделение условия и заклю­чения, замену терминов определением, получение следствий и т. д., так и в целом решение от условия к заключению и от заклю­чения к условию. Применение граф-схем при решении геометри­ческих задач эффективно в том случае, если учащиеся уже встре­чались с граф-схемами при решении арифметических задач.

Вопросы и задания

1. Приведите определения понятия задача.

2. Укажите функции задач в обучении.

3. Приведите примеры математических задач, несущих в себе информацию из различных отраслей знаний.

4. Приведите примеры задач, выполняющих различные дидак­тические функции на уроке.

5. Укажите, какие недостатки имеют место при обучении уча­щихся решать задачи.

6. Сформулируйте определение приема решения задачи, укажи­те возможности классификации приемов решения задач.

7. Приведите примеры задач, в основе поиска идеи решения ко­торых используются эвристики: а) восходящий анализ; б) переформатирование; в) аналогия; г) суперпозиция; д) выделе­ние подзадач внутри одной задачи; е) рассмотрение частных случаев; ж) обобщение.

8. Продумайте организацию деятельности учащихся на уроке по поиску идеи решения задачи с помощью различных эвристик.

9. Продумайте этапы обучения учащихся различным эвристи­кам.

10. Разработайте методику обучения учащихся: а) восходящему анализу; б) переформулированию; в) выделению подзадач на различных этапах обучения.

11. Выделите типы арифметических, алгебраических, планимет­рических, стереометрических, тригонометрических задач.

12. Разработайте прием обучения учащихся решению задач на дробь от числа, числа по дроби и отношение двух чисел.

13. Разработайте прием решения задач на пропорциональные за­висимости.

14. Разработайте методику формирования приема решения ал­гебраических задач с помощью составления уравнений.

15. Разработайте методику формирования приема решения задач на различные признаки равенства треугольников.

16. Приведите примеры алгоритмов, содержащихся в определе­ниях, формулировках теорем, правилах.

17. Разработайте алгоритм записи обыкновенной дроби, знаме­натель которой равен единице с нулями, в виде десятичной и обратно.

18. Разработайте алгоритм вычитания смешанных чисел, орга­низуйте его закрепление.

19. Представьте правило нахождения степени произведения в алгоритмической форме.

20. Опишите, в чем заключается компактный метод Я. И. Груде-нова при работе над применением определений, правил, фор­мулировок теорем. Приведите примеры,

21. Разработайте фрагмент урока по проведению анализа усло­вия арифметической, алгебраической, планиметрической, сте­реометрической задачи.

22. Разработайте план обучения учащихся умению анализировать условие задачи при решении арифметических, алгебраичес­ких, геометрических задач.

23. Продумайте организацию деятельности учащихся на всех эта­пах решения выбранной задачи.

24. Продумайте возможности обучения приему получения след­ствий при решении арифметических, алгебраических, геомет­рических задач.

25. Укажите формы проверки идеи решения задачи.

26. Укажите формы проверки исполнительной части действия при решении задачи.

27. Разработайте образцы записи решения арифметической, алгеб­раической, планиметрической и стереометрической задачи.

28. Выполните поиск решения арифметической и планиметричес­кой задачи в виде граф-схем.

29. В приеме решения задач с помощью составления уравнений выделите операции, которые необходимо формировать специ­ально и разработайте систему заданий для их формирования.

Литература

1. Адамар Ж. Исследование психологии процесса изобретения в области математики. М.: Советское радио, 1970.

2. Алътшуллер ГС. Основы изобретательства. М., 1964.

3. Байдак А.В., Ефимов В. И., Лапчик МП. Формирование ал­горитмической культуры у учащихся // Повышение эффектив­ности обучения математике в школе. М.: Просвещение, 1989.

4. Валиев С. Индивидуальные задания по устранению ошибок / / Математика в школе. 1989. № 5.

5. Виноградова Л.В. Развитие мышления учащихся при обуче­нии математике. Петрозаводск, 1989.

6. Виноградова Л. В. Об использовании предписания при реше­нии задач на составление уравнений // Математика в школе. 1994. №4.

7. Виноградова Л.В., Домашенко М.М. Как подготовить и про­вести проблемную беседу // «Математика». 1994. № 24.

8. Григорьева Т.П., Иванова Т. А., Кузнецова Л.И., Перевощи-кова Е. И. Основы технологии развивающего обучения мате­матике. Н. Новгород, 1997.

9. Груденов Я.И. Психолого-педагогические основы обучения математике. М.: Педагогика, 1987.

10. Заикин М.И., Колосова В.А. Провоцирующие задачи // Ма­тематика в школе. 1997. № 6.

11. Кабапова-Меллер Е.Н. Формирование приемов умственной деятельности и умственное развитие учащихся. М.: Просве­щение, 1968.

12. Колягин Ю.М., Оганесян В.А. Учись решать задачу. М.: Про­свещение, 1980.

13. Кулюткин Ю. Н. Эвристические методы в структуре решения. М.: Просвещение, 1970.

14. ЛандаЛ.Н. Алгоритмизация в обучении. М.: Просвещение, 1966.

15. Манвелов С.Г. Задачи по математике на развитие самоконт­роля учащихся. М.: Просвещение, 1997.

16. Монахов В.М., Лапчик М.Н. Формирование алгоритмичес­кой культуры школьника при обучении математике: Пособие для учителя. М.: Просвещение, 1978.

17. Методика преподавания в средней школе: Общая методика / Сост. Р.С. Черкасов, А.А. Столяр. М.: Просвещение, 1985.

18. Нешков К.И., Семушин А.Д. Функции задач в обучении // Математика в школе. 1971. № 3.

19. Оганесян В. А., Колягин Ю.М. и др. Методика преподавания математики в средней школе. М.: Просвещение, 1980.

20. ПойаД. Как решать задачу. М.: Учпедгиз, 1961.

21. ПойаД. Математическое открытие. М.: Наука, 1970.

22. Рогановский ЕВ. Решение текстовых задач в IV-V классах // Математика в школе. 1987. № 4.

23. Рогановский Е. В. Методика преподавания математики в сред­ней школе. Минск: Вышейшая школа, 1980.

24. Рыжик В. И. Формирование потребности в самоконтроле при обучении математике // Математика в школе. 1980. № 3.

25. Саранцев Г. И. Упражнения в обучении математике. М.: Про­свещение, 1995.

26. Тихомиров O.K. Психология мышления^ М.: Изд-во МГУ, 1984.

27. Фридман Л. М. Учитесь учиться математике. М.: Просвеще­ние, 1986.

28. Фридман Л.М., Турецкий Е.Н., Стеценко В.Я. Как научить­ся решать задачи. М.: Просвещение, 1989.

29. ЦикарьА.Я. Схематизация и моделирование при решении за­дач // Математика в школе. 1998. № 3.

30. Эсаулов А.Ф. Активизация учебно-познавательной деятель­ности студентов. М.: Высшая школа, 1982.

31. Тарасенкова НА. Найдите ошибку // Математика в школе. 1997. №2.