Методи вирішення задач на власні значення та власні вектори матриць

Вирішення задач на власні значення широко використовуються в різних розділах математики, фізики та техніки. Наприклад, при знаходженні спектру атома водню постає задача вирішення диференційного рівняння другого порядку і т. д. В курсах теорії коливань та квантової механіки є багато прикладів, з яких видно, що в залежності від постановки задачі власні значення можуть існувати або не існувати, бути дійсними або комплексними; спектр власних значень може бути дискретним, неперервним, складатися зі смуг або бути комбінацією перелічених випадків.

Розглянемо матрицю в - вимірному дійсному просторі векторів .

Власним вектором матриці називається ненульовий вектор , що задовольняє рівність:

, (8.15)

де - власне значення матриці , що відповідає власному вектору.

Власні значення матриці з дійсними елементами можуть бути дійсними різними, дійсними кратними, комплексними попарно спряженими, комплексними кратними.

Класичний спосіб знаходження власних значень і власних векторів полягає в наступному:

- для однорідної системи лінійних алгебраїчних рівнянь (СЛАР), отриманої з (8.15) , , ненульові рішення ( , а саме такі рішення і знаходять) мають місце за умови:

, (8.16)

причому рівняння (8.16) називають характеристичним рівнянням, а вираз в лівій частині – характеристичним багаточленом;

• будь-яким способом знаходять рішення 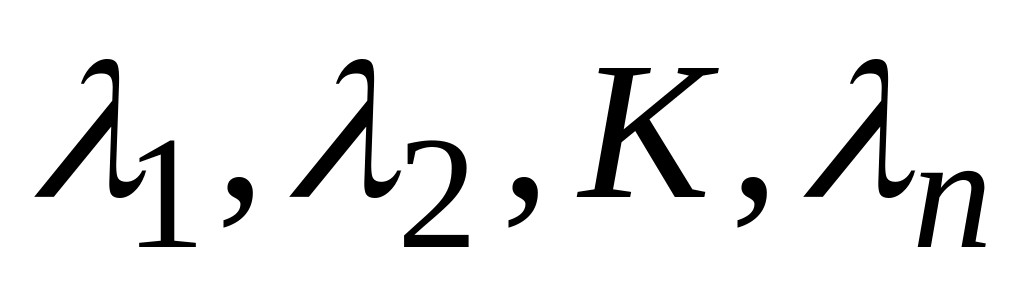алгебраїчного рівняння (8.16) -го степеня (припустимо, що вони дійсні і різні);

• розв’язуючи однорідну СЛАР виду (8.16) для різних власних значень 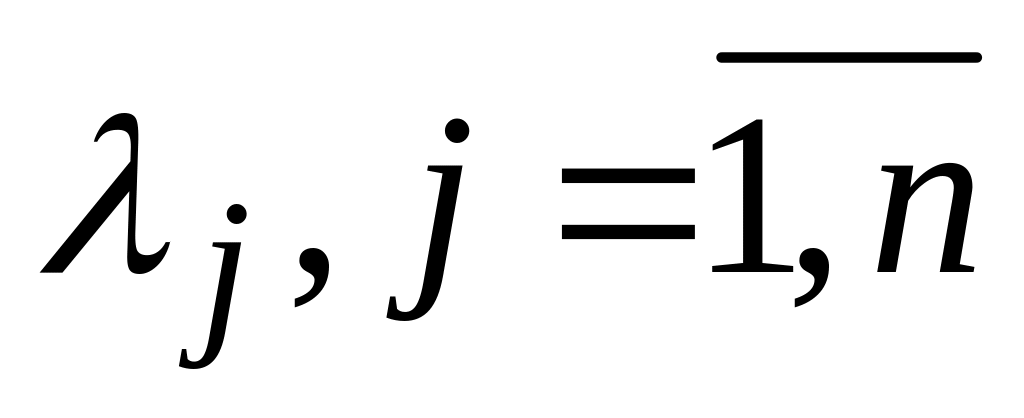, , 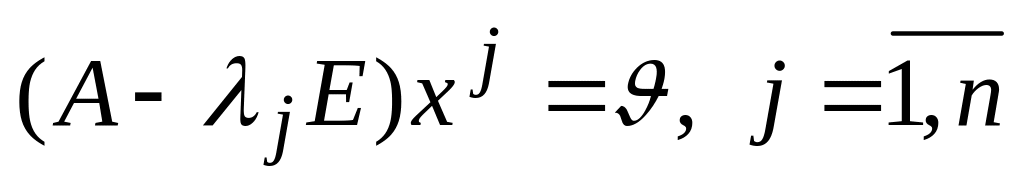одержуємо лінійно незалежні власні вектори 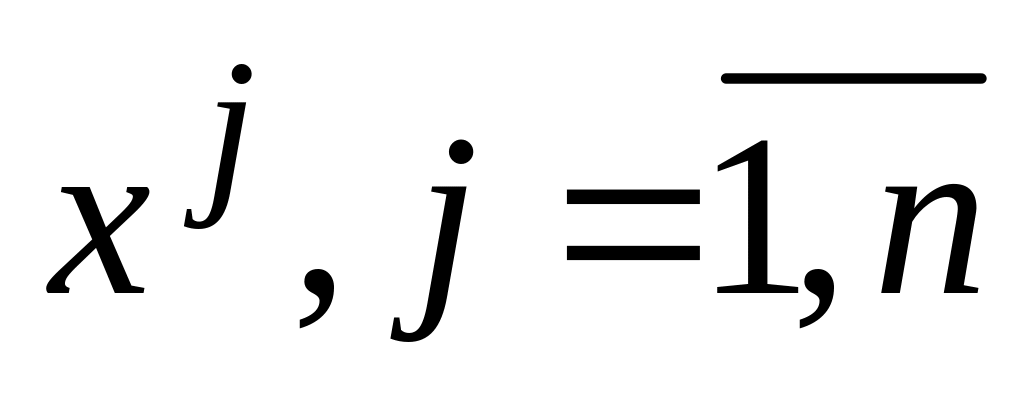, що відповідають власним значенням .

Попарно різним власним значенням відповідають лінійно незалежні власні вектори. Якщо кількість лінійно незалежних власних векторів матриці співпадає з розмірністю простору , то їх можна прийняти за новий базис, в якому матриця прийме діагональний вигляд:

, (8.17)

на головній діагоналі котрої знаходяться власні значення, а стовпці матриці перетворення є власними векторами матриці . Матриці та , що задовольняють рівності (8.17), називають подібними. Власні значення подібних матриць та співпадають.

Метод обертань Якобі чисельного вирішення задач на власні значення та власні вектори матриць

Метод обертань Якобі застосовується тільки для симетричних матриць і вирішує проблему власних значень та власних векторів таких матриць. Він базується на відшуканні, за допомогою ітераційних процедур, матриці в перетворенні подібності , а оскільки для симетричних матриць матриця перетворення подібності є ортогональною , то , де - діагональна матриця з власними значеннями на головній діагоналі:

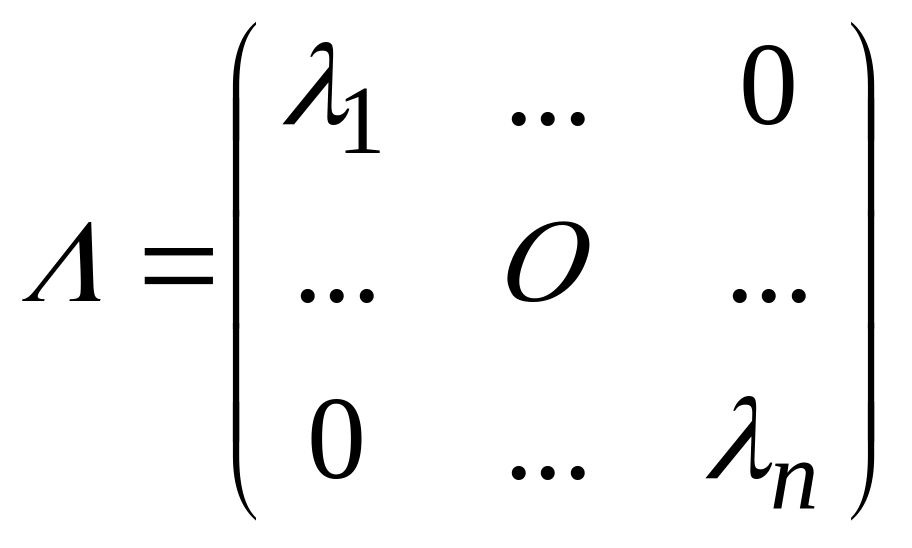. (8.18)

Якщо задана симетрична матриця і необхідно для неї обчислити з точністю всі власні значення і відповідні їм власні вектори, то алгоритм методу обертань виглядає наступним чином.

Нехай відома матриця на -й ітерації, при цьому для .

1. Обирається максимальний по модулю недіагональний елемент 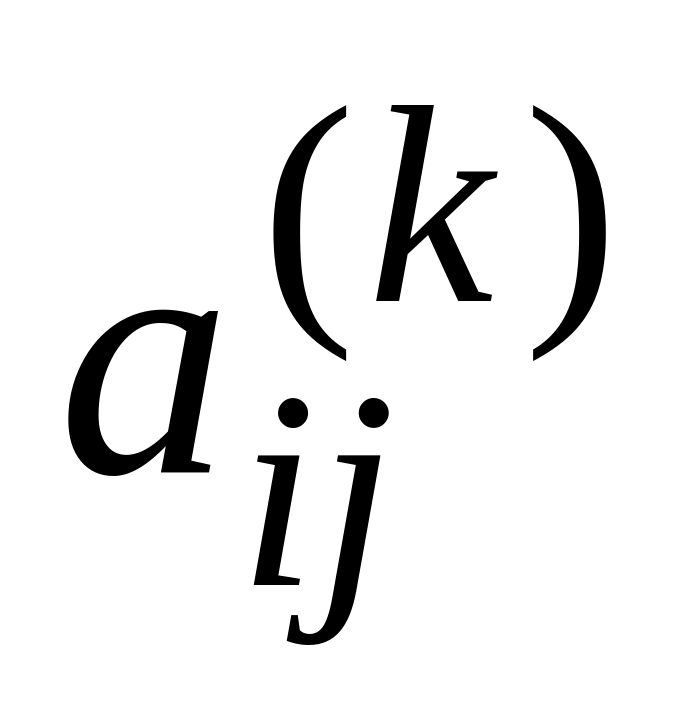матриці .

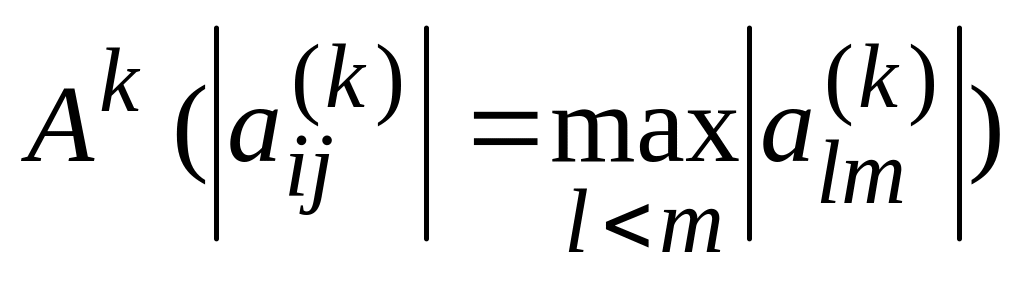2. Ставиться задача знайти ортогональну матрицю 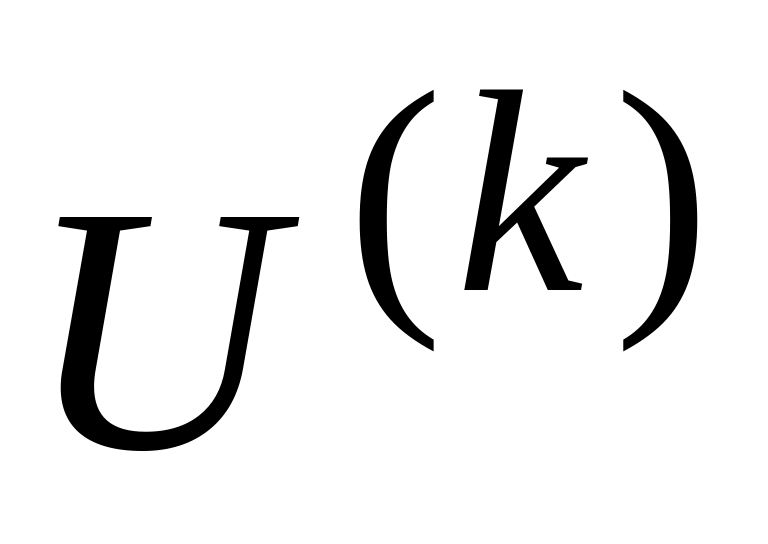, щоб в результаті перетворення подібності 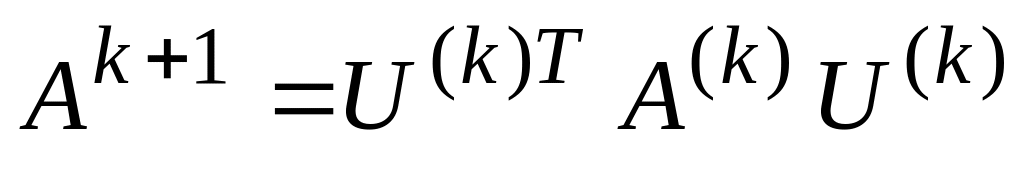відбулось обнулення елемента 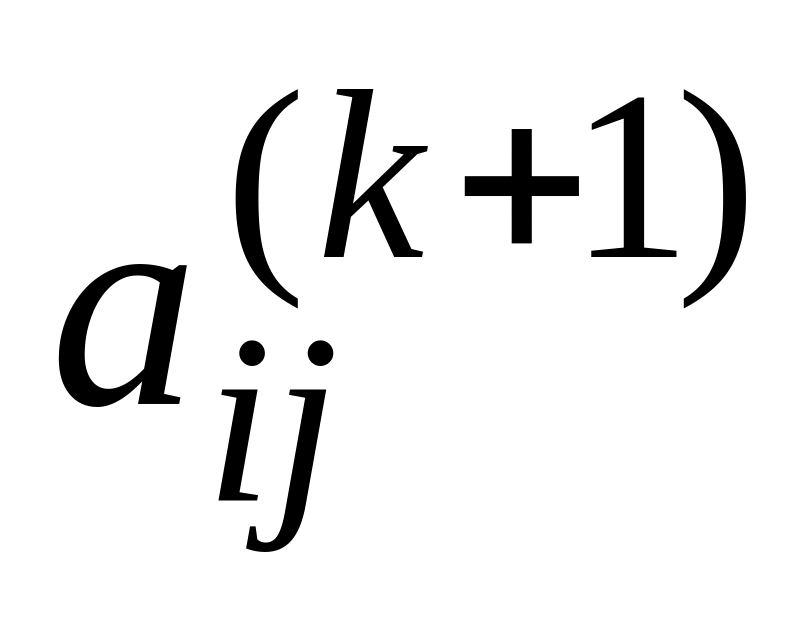матриці 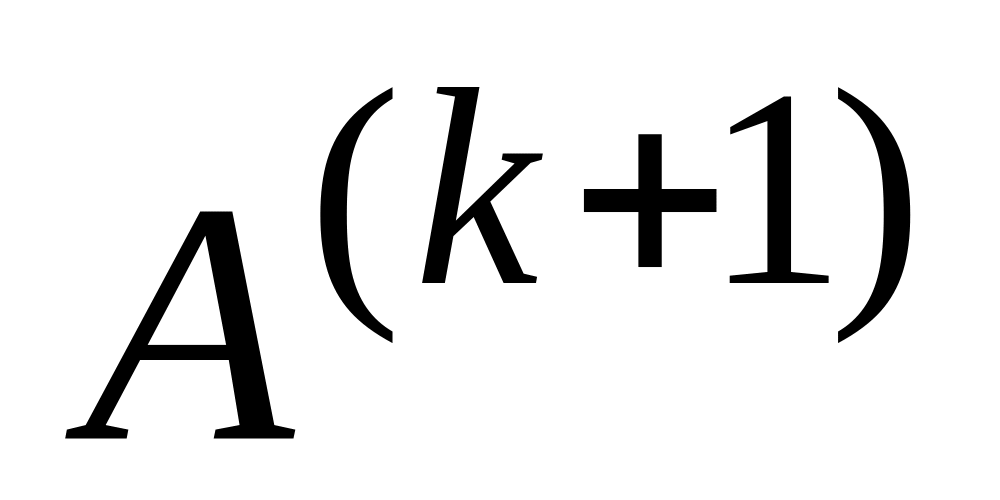. В якості ортогональної матриці обирається матриця обертання виду (8.18):

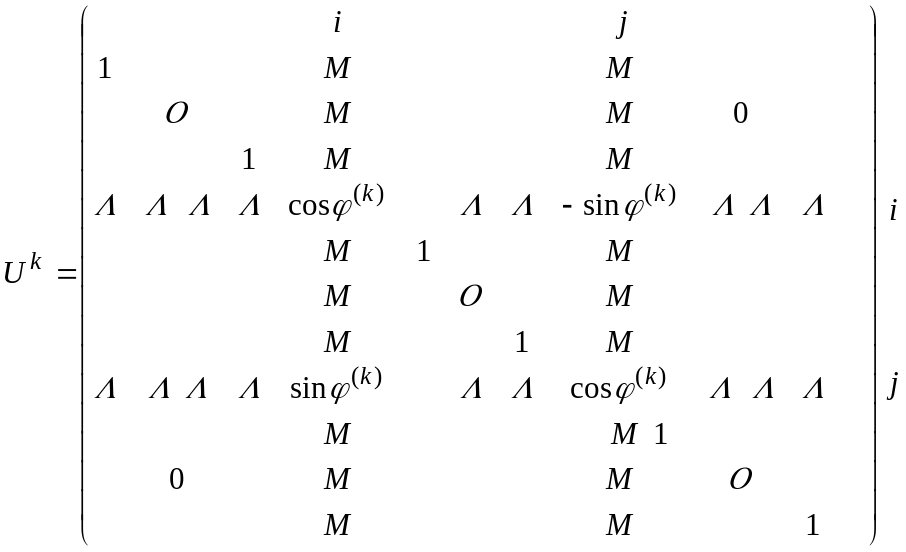, (8.19)

В матриці обертання (8.19) на перетині -го рядка та -го стовпця знаходиться елемент , де - кут обертання, що підлягає визначенню. Симетрично відносно головної діагоналі (на перетині -й рядок та -й стовпець) розташований елемент . Діагональні елементи та дорівнюють відповідно , , інші діагональні елементи . Інші елементи в матриці обертання дорівнюють нулю.

Кут обертання визначається з умови :

,

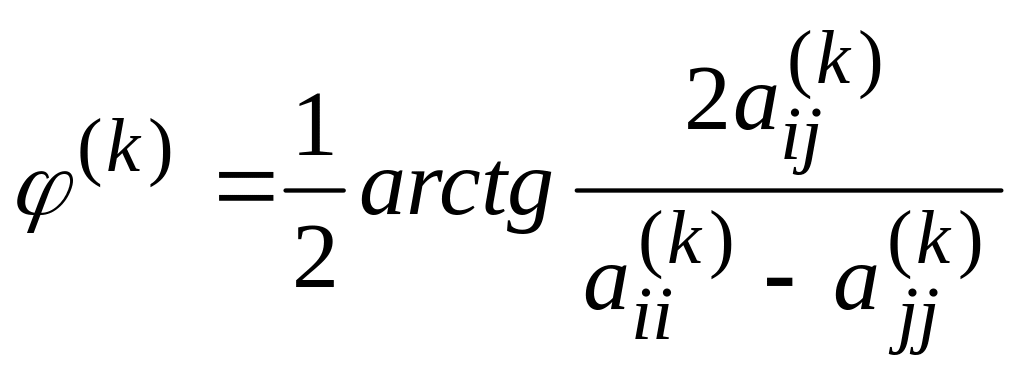причому, якщо , то .

3. Будується матриця :

,

в якій елемент .

В якості критерію закінчення ітераційного процесу використовується умова зменшення суми квадратів позадіагнальних елементів:

.

Якщо , то ітераційний процес:

продовжується. Якщо , то ітераційний процес зупиняється, і в якості шуканих власних значень приймаються:

.

Координатними стовпцями власних векторів матриці в одиничному базисі будуть стовпці матриці , тобто:

причому ці власні вектори між собою будуть ортогональними, тобто: .

Приклад 8.3

З точністю обчислити власні значення та власні вектори матриці:

.

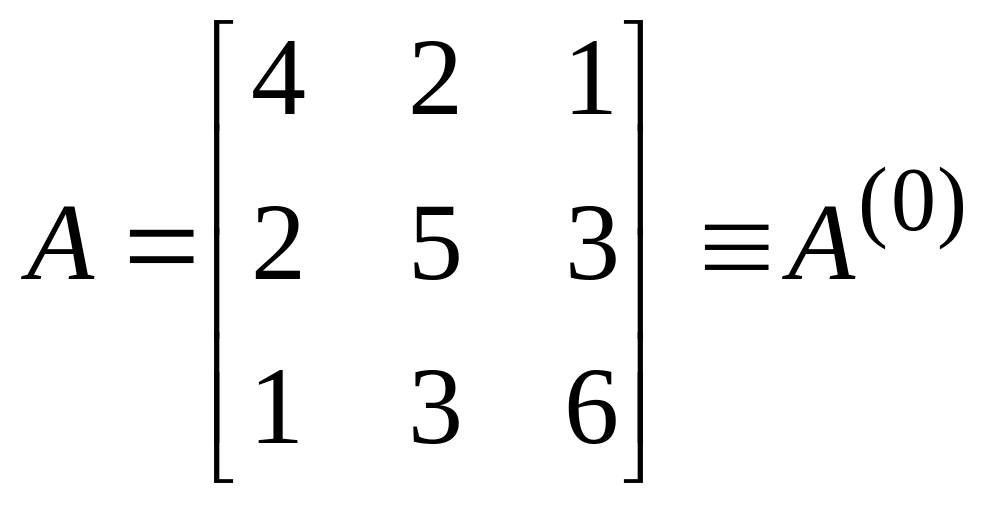Обираємо максимальний за модулем позадіагнальний елемент матриці , тобто знаходимо , такий, що . Ним є елемент .

Знаходимо матрицю обертання, що відповідає цьому елементу:

;

.

Обчислюємо матрицю :

.

В одержаній матриці з точністю до помилки округлення елемент .

, отже ітераційний процес необхідно продовжити.

Переходимо до наступної ітерації ( ):

; .

;

;

.

.

Переходимо до наступної ітерації ( ):

; .

;

;

.

Таким чином, у якості шуканих власних значень можуть бути прийняті діагональні елементи матриці :

Власні вектори визначаються з добутку:

;

Одержані власні вектори ортогональні в межах заданої точності, тобто: