Завдання

Обчислити значення інтеграла за методом прямокутників, трапецій та Сімпсона з розбиттям відрізка інтегрування на 4 рівні частини (табл. 6.1).

Таблиця 6.1

Варіант	Підінтегральна функція	Межі інтегрування
1	2	3	4
1		5	6,5
2		2	3,5
3		3	3,5
4		0	2
5		0,5	2
6		2	2,5
7		0	1
8			2
9		2	5

Продовження таблиці 6.1

1	2	3	4
10		0,2	0,3
11		0
12		0	2
13		0
14		1	2
15		0	1
16		0	2
17		0	1
18		0,5	1
19		0
20		0
21		0,1	0,5
22		1	2

Контрольні питання

1. Сутність чисельних методів інтегрування.

2. Як визначається на практиці похибка чисельного інтегрування?

3. Який порядок точності має метод прямокутників?

4. В яких випадках застосовується метод трапецій?

5. Чи можна методами прямокутників та трапецій отримати точне значення інтегралу?

6. Якою апроксимуючою функцією замінюється підінтегральна функція у методі Сімпсона?

7. Як визначаються похибки основних квадратурних формул?

8. Чи є постійними вагові коефіцієнти в формулі Ньютона-Котеса?

9. При яких методах інтегрування значення розташовуються рівномірно?

10. Як оцінити похибку інтегрування в методах Чебишева та Гауса?

Практична робота № 7

Тема: Диференційні рівняння. Метод Ейлера. Метод Рунге-Кутта. Метод Мілна

Теоретичні відомості Метод Ейлера і модифікований метод Ейлера

Метод Ейлера – один з найпростіших методів вирішення диференційних рівнянь першого порядку:

. (7.1)

При практичних розрахунках він дає значну похибку, оскільки похибка методу Ейлера на кожному кроці є величина порядку . Точність методу досить мала, і з переходом від точки до точки похибка систематично зростає.

Обчислювальний алгоритм його подається наступним чином:

,

де - крок по (у загальному випадку може бути непостійним).

Застосування методу починається з початкових умов .

Для підвищення точності на практиці використовують модифікований метод Ейлера другого порядку. Алгоритм:

.

Тут у формулі використовується значення , з поки що невідомим значенням . Це значення може бути знайдене попередньо, наприклад, за методом Ейлера, а потім використане у алгоритмі.

Приклад 7.1

Вирішити дифенційне рівняння виду при початкових умовах з кроком на інтервалі .

Перший крок:

.

Другий крок:

.

Наведемо останні результати за наведеною формулою (через точку) у табл. 7.1

Таблиця 7.1

	0	0,2	0,4	0,6	0,8	1,0
Рішення	1	1,4420	2,1041	3,1183	4,6747	7,0472

Це рівняння має аналітичне рішення .

Приклад 7.2

Вирішити дифенційне рівняння виду при початкових умовах з кроком на інтервалі .

Перший крок за методом Ейлера:

.

Перший крок за модифікованим методом:

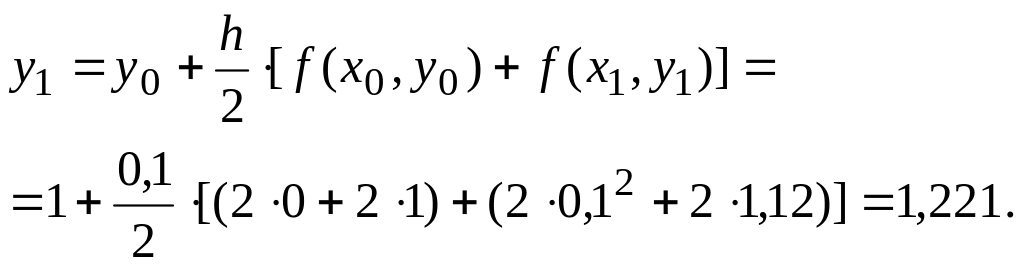
Другий крок за методом Ейлера:

Другий крок за модифікованим методом:

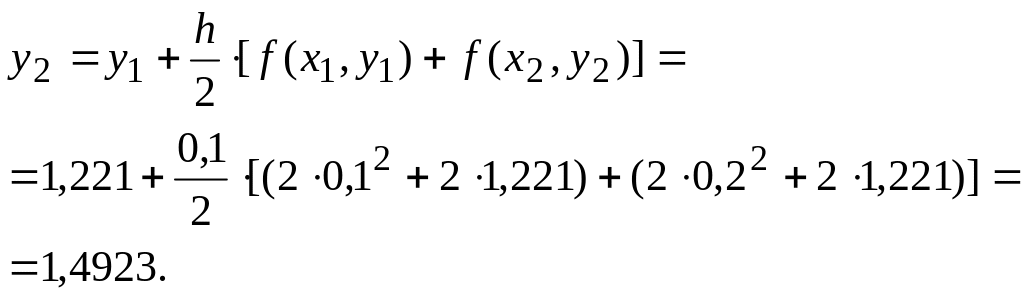
Результати подальших кроків (через точку представимо у табл. 7.2

Таблиця 7.2

	0	0,2	0,4	0,6	0,8	1,0
Рішення	1	1,4923	2,2466	3,4176	5,2288	8,0032