Метод Сімпсона

У цьому методі функцію, що інтегрується, на кожному малому інтервалі заміняють параболою, що з'єднує три точки кривої - на краях і посередині цього інтервалу (використовується поліном другого степеня). Розрахунок проводиться за квадратурною формулою Сімпсона для обчислення площі під ділянкою параболи (рис. 6.3).

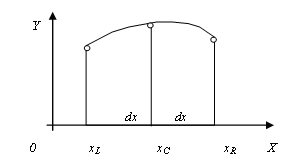
Рис. 6.3. Ілюстрація методу Сімпсона

,

де - значення ліворуч, у центрі і праворуч для малого інтервалу.

З використанням цієї залежності при додаванні одержимо:

,

тобто відбувається додавання крайніх значень функції, проміжних (з чергуванням коефіцієнтів - 2 чи 4), а потім отримана сума збільшується на третину довжини напівінтервалу ( ). Число напівінтервалів повинно бути парним. Метод Сімпсона має четвертий порядок точності.

Практична оцінка похибки проводиться за формулою:

тобто, при збільшенні числа розбиттів у два рази похибка зменшується у 15 разів.

Приклад 6.3

Обчислити .

Розв’язок:

1) метод Сімпсона для всього інтервалу, , , , :

3. метод Сімпсона з поділом інтервалу на 4 частини, :

Метод Ньютона-Котеса

Даний метод є узагальненням попередніх, побудований на аналогічних принципах і припускає заміну підінтегральної функції параболою -ro порядку (а не другого, як у методі Сімпсона). Розрахункова формула для однієї ділянки інтегрування:

де , , , - коефіцієнти Ньютона-Котеса, a - число ординат, що використовуються, на ділянці (починаючи з 0) і застосовуються для апроксимації підінтегральної функції. Природно, що для заміни параболою третього степеня буде потрібно вже чотири точки, а четвертого - п'ять точок. Коефіцієнти , не залежать від функції і визначені заздалегідь. Деякі з них наведені нижче.

Усі попередні формули є частковим випадком формули Ньютона-Котеса. Зокрема, при одержуємо метод трапецій (для однієї ділянки), при - формулу Сімпсона. Не слід брати , тому що при великих значеннях алгоритм виявляється нестійким.

При розбитті всього інтервалу на ділянок формулу потрібно застосовувати для кожної ділянки, а результати додати.

Приклад 6.4

Обчислити .

Оберемо :

Методи Чебишева і Гауса

Усі попередні методи мали наступну особливість: значення розташовувалися рівномірно, а вагові коефіцієнти були різними (у загальному випадку, хоча деякі з них були рівні один одному). У методі Чебишева прийняті усі вагові коефіцієнти однаковими, а - різними. Попередньо при використанні наведених нижче формул методу варто перетворити змінну інтегрування, привівши її до діапазону [-1; 1] у такий спосіб:

.

Розрахункові формули виходять для різних значень (кількість ординат, що використовуються при розрахунках на одній ділянці), виходячи із забезпечення можливості інтегрування без помилки полінома як можна більш високого степеня. Виявляється, можна інтегрувати поліном без помилки при . Для цього вже розраховані необхідні параметри. Частина з них наведена нижче.

З урахуванням перетворення змінної формула інтегрування буде виглядати так:

У методі Гауса на відміну від методу Чебишева всі значення в точках - різні і усі вагові коефіцієнти - різні. Це дозволило забезпечити інтегрування без помилки вже полінома степеня , що і для будь-яких інших, не поліноміальних підінтегральних функцій дає кращі результати (тобто меншу помилку). Деякі значення параметрів формули інтегрування наведені нижче.

З урахуванням перетворення змінної формула інтегрування за методом Гауса буде виглядати так:

.

Слід зазначити, що в цих методах внаслідок нерівномірного кроку інтегрування не можна оцінити похибку інтегрування подвійним прорахунком. Для цієї мети застосовуються інші алгоритми.

Приклад 6.5

Обчислити .

Оберемо ,

, ,

відповідно :

1. для методу Чебишева одержимо:

;

2. для методу Гауса одержимо: