Максимум та мінімум (екстремум) функції

Значення функції f(x) в точці х₀ називається максимумом (мінімумом), якщо воно є найбільшим (найменшим) у порівнянні з її значеннями в усіх достатньо близьких точках зліва та справа від х₀.

Функція може мати екстремум (максимум чи мінімум) тільки в тих точках, які лежать в області визначення функції і де її похідна дорівнює нулю або не існує. Такі точки називаються критичними.

У відповідних точках графіка функції дотична паралельна до осі Ох (у = 0), або осі ординат (у = ).

На графіку функції (рис. 5.1) добре видно, що точками екстремуму є всі точки, де функція змінює свою поведінку та неперервна.

Точки х1 и х4, при переході через які аргумента х зростання функції змінюється на спадання, є точками максимуму, а точки х3 и х6, при переході через які аргумента х спадання змінюється на зростання, є точками мінімуму.

Так як поведінка функції характеризується знаком її похідної, то функція буде мати екстремум в тих точках, де її похідна змінює знак, а сама функція неперервна.

Звідси витікає наступне правило дослідження функції на екстремум

Щоб знайти точки екстремуму функції у=f(x), в яких вона неперервна, треба:

І. Знайти похідну у' та критичні точки, в яких у=0 або не існує, а сама функція неперервна, і які лежать в області визначення функції.

ІІа. Визначити знак у' зліва та справа від кожної критичної точки.

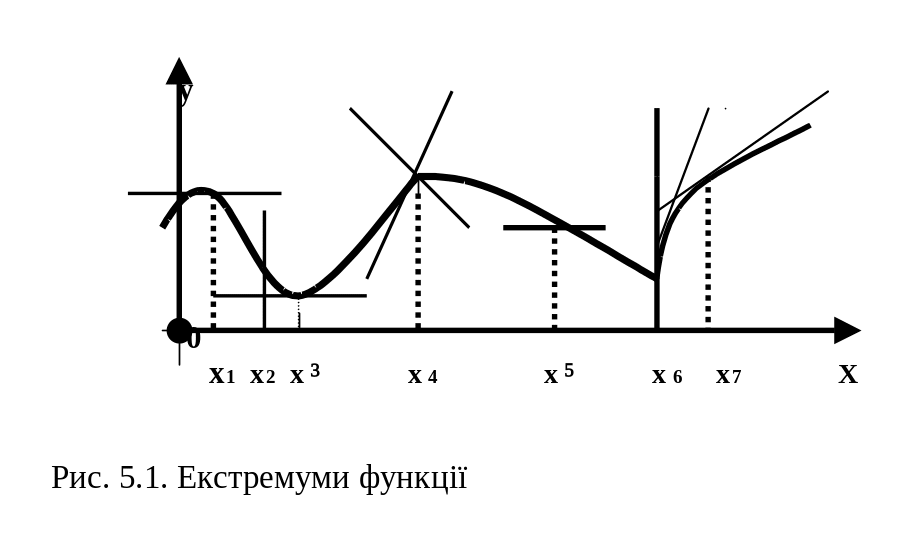
Якщо при переході аргументу х через критичну точку х₀:

• у' змінює знак з + на – , то х₀ є точкою максимуму;

• у' змінює знак з – на + , то х₀ є точкою мінімуму;

• y' не змінює знака, то в точці х₀ нема екстремуму.

Іноді легше досліджувати критичні точки, де у'=0, по знаку другої похідної, — замість правила IIа можна використовувати наступне правило:

IIб. Знайти другу похідну у'' і визначити її знак в кожній критичній точці.

Якщо в критичній точці х₀, де у=0

• у'' > 0, то х₀ -- точка мінімуму;

• у'' < 0, то х₀ – точка максимуму;

• у'' = 0, то питання про наявність екстремуму в точці х₀ залишається відкритим. Таку критичну точку, як і будь-яку іншу, можна досліджувати по правилу IIa.

Далі треба знайти екстремуми функції, тобто обчислити значення функції в знайдених точках екстремуму.

При дослідженні на екстремум деяких типів функцій можливі значні спрощення. Наприклад, якщо функція являє собою дріб з постійним чисельником або корінь з цілим додатнім показником.

Найбільше та найменше значення функції

Найбільшим значенням функції називається саме більше, а найменшим значенням – саме менше з усіх її значень.

Функція може мати тільки одне найбільше значення і тільки одне найменше значення або може не мати їх зовсім. Наприклад, в усій своїй області визначення функція sin x має найбільше значення, рівне одиниці, та найменше значення, рівне мінус одиниці; функції tg x та х³ не мають ні найбільшого, ні найменшого значення; функція –х² має найбільше значення, рівне нулю, але не має найменшого значення; функція має найменше значення, рівне одиниці, але не має найбільшого значення ( рис. 5.2).

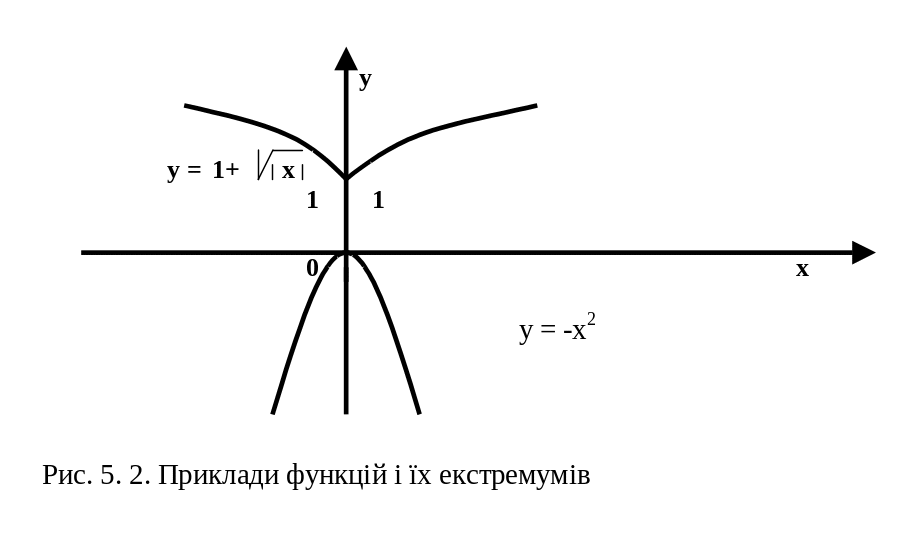
Знаходження найбільшого і найменшого значення неперервних функцій базується на наступних властивостях цих функцій:

1. Якщо в деякому інтервалі функція f(x) неперервна і має тільки один екстремум і якщо це максимум (мінімум), то він буде найбільшим (найменшим) значенням функції в цьому інтервалі.

2. Якщо функція f(x) неперервна на деякому відрізку [a,b], то вона обов’язково має на цьому відрізку найбільше та найменше значення. Ці значення досягаються нею або в точках екстремуму, що лежать всередині відрізка, або на границях цього відрізка .

Звідси витікає практичне правило для знаходження найбільшого або найменшого значення функції f(x) на відрізку [a,b], де вона неперервна:

• знайти критичні точки, що лежать всередині відрізку [a,b], і обчислити значення функції в цих точках. Обчислити значення функцій на кінцях відрізка, тобто f(a) и f(b).

• порівняти отримані значення функції: саме більше з них буде найбільшим значенням, а саме менше – найменшим значенням функції на усьому даному відрізку.