№47. Теорема Бернулі (закон великих чисел у формі Бернулі).

Теорема. Якщо імовірність події в n дослідах стала і дорівнює р, то ймовірність відхилення відносної чатоти від цієї ймовірності на величину не більшу за  як завгодно близька до одиниці при достатньо великому n: при , або .

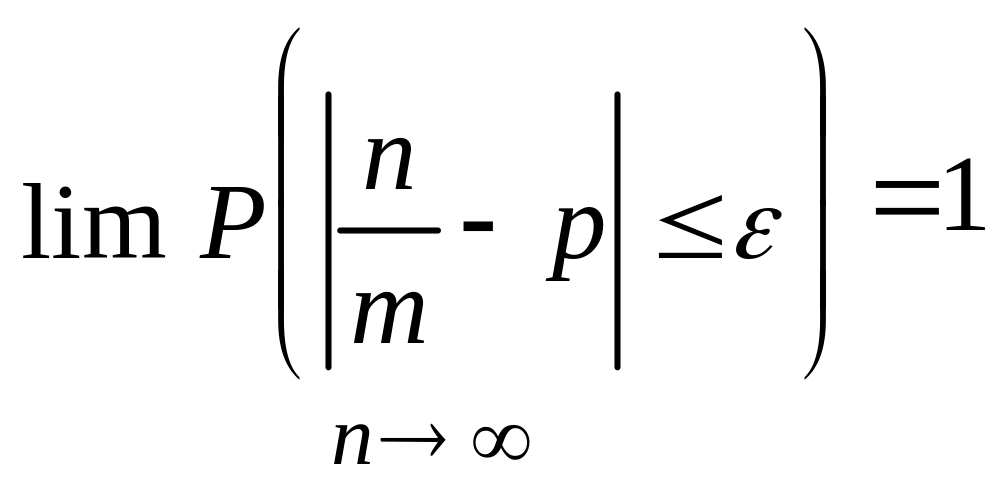Доведення. Нехай – випадкова величина, яка приймає значення 1, якщо при досліді настає певна подія, і значення 0 – якщо подія не настає, тобто: . Тоді маємо ряд розподілу

хi	1	0
рi	p	q

Де .

Оскільки випадкові величини Х_i мають обмежену дисперсію, то можна можна використати теорему Чебишова:

=1.

Дріб дорівнює відносній частоті. Дійсно, кожна з величин Х₁, Х₂,…,Х_n з появою події в досліді приймає значення 1. звідси сума Х₁+Х₂+…+Х_n дорівнює m – кількості появ події в n дослідах. М(Х₁)+М(Х₂)+…+М(Х_n)=np. Таким чином . Теорема доведена.

48. Теорема Ляпунова (закон больших чисел в форме Ляпунова).

Доповнює закон великих чисел. (Закон великих чисел обєднує кілька теорем, у кожній з яких за певних умов виявляється факт наближення середніх характеристик під час проведення великої кількості експериментів до певних невипадкових, сталих величин)..

Теорема: Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

На практике для большинства случайных величин выполняются условия теоремы Ляпунова.

Условие Ляпунова при некотором 

Для нормированных величин условие Ляпунова:

Условие Ляпунова при 1

Условие Ляпунова при 2

Основні висновки із закону великих чисел: при достатньо великій кількості дослідів можна вважати, що випадкова величина має розподіл близький до нормального (висновок теореми Ляпунова), при цьому за матиматичне сподівання випадкової величини можна брати середнє вибіркове (теорема Чебишова), а за ймовірність події – відносну частоту (теорема Бернулі).

49. Случайный марковский процесс. Матрица перехода.

марковский процесс – это случайный процесс, обладающий марковским свойством.

марковским свойством называется свойство, состоящее в том, что условная плотность зависит только от значения процесса в последний момент времени, т. е. для всех n2.

Марковский процесс называется однородным, если

P_T1,T2(x,A)=P(t₂-t₁,x,A).

Однородной называется цепь Маркова, если условная вероятность p_ij перехода системы из состояния i в состояние j не зависит от номера испытания. Вероятность p_ij называется переходной вероятностью.

Полная вероятностная картина возможных изменений, осуществляющихся при переходе от одного испытания к следующему, задается матрицей, составленной из вероятностей перехода, которая называется матрицей перехода.

1. Элементы матрицы должны быть неотрицательными числами, т.е. при всех i и j

0 p_ij 1

2. Сумма элементов каждой строки матрицы перехода равна единице.

Матрицы, суммы элементов всех строк которых равны единице, называются стохастическими. Если при некотором п все элементы матрицы Р^п не равны нулю, то такая матрица переходов называется регулярной. Регулярные матрицы переходов задают цепь Маркова, в которой каждое состояние может быть достигнуто через п шагов из любого состояния. Такие цепи Маркова также называются регулярными.

На основе матрицы перехода системы можно построить так называемый граф состояний системы, его еще называют размеченный граф состояний. Это удобно для наглядного представления цепи.

Равенство Маркова: , где – шагов. , .  . , .